Conservación de la energía en el movimiento de rotación
En la página titulada Dinámica de un sistema de partículas en el apartado 'Energía de un sistema de partículas' demostramos que el trabajo de las fuerzas exteriores Wext se invierte en modificar la energía U de un sistema de partículas.
La energía de un sistema de partículas es la suma de la energía cinética de todas las partículas más la energía potencial de interacción de cada par de partículas, en ese apartado, consideramos un sistema de dos y de tres partículas. Para un sistema de N partículas, se escribe
Para un sólido rígido, el segundo término no cambia, permanece constante, y el primer término es la energía cinética de rotación de un sólido rígido de momento de inercia I, alrededor de un eje fijo con velocidad angular ω.
El trabajo de las fuerzas aplicadas al sólido rígido, se invierte en modificar la energía cinética de rotación.
Si la fuerza (o fuerzas) exterior es conservativa (por ejemplo, el peso). El trabajo de la fuerza exterior es igual a la variación de energía potencial. Del mismo modo que un cuerpo que se deja caer, o se lanza hacia arriba, parte de la energía potencial se transforma en energía cinética o bien, parte de la energía cinética se transforma en potencial. En este caso, parte de la energía potencial se transforma en energía cinética de rotación o viceversa.
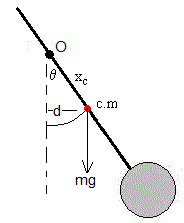
Supongamos un sólido rígido que gira alrededor de un eje fijo, principal de inercia, perpendicular al plano de la pantalla y que pasa por el punto O. Se separa un ángulo θ0 de la posición de equilibrio estable y se suelta, vamos a aplicar el principio de conservación de la energía para calcular la velocidad angular del sólido cuando pasa por la posición de equilibrio estable.
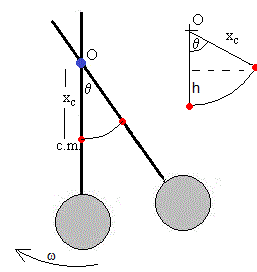
Sea I el momento de inercia del sólido rígido respecto del eje que pasa por O, y sea xcm, la posición del centro de masa (c.m.) medida desde O.
Sabiendo que el peso del cuerpo mg actúa en el centro de masa. El trabajo del peso es igual a la variación de energía potencial mgh, siendo h el cambio de altura del centro de masa (que describe un arco de circunferencia de radio xcm y ángulo θ, tal como vemos en la figura
h=xcm-xcmcosθ
La energía potencial del c.m. disminuye y aumenta la energía cinética de rotación
Este es el principio de conservación de la energía para un sólido en rotación alrededor de un eje fijo.
Ejemplo
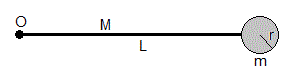
Sea una varilla uniforme de longitud L y masa M con un disco de masa m y radio r soldado en su extremo. El sistema puede girar alrededor de un eje horizontal que pasa por el otro extremo de la varilla. La varilla parte del reposo desde la posición θ=π/2. Cuando la posición de la varilla es θ, determinar:
- la velocidad angular
- la aceleración angular
- la fuerza que ejerce el eje
La posición xc del centro de masas y el momento de inercia I0 del conjunto respecto a un eje perpendicular que pasa por O es
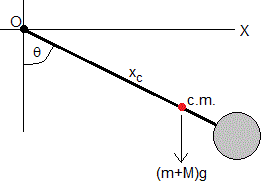
Aplicamos el principio de conservación de la energía para calcular la velocidad angular de rotación ω. Tomamos el nivel cero de energía potencial en el eje X
Aplicamos la ecuación de la dinámica de rotación para calcular la aceleración angular α. El momento del peso respecto de O, es igual al momento de inercia por la aceleración angular
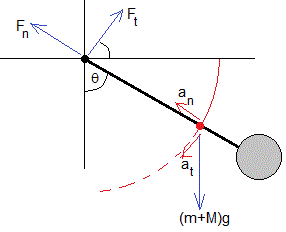
El eje ejerce dos fuerzas, mutuamente perpendiculares, Ft y Fn cuyo valor vamos a calcular, conocida la aceleración angular α y la velocidad angular ω
El centro de masas describe un arco de circunferencia de radio xc.
La ecuación del movimiento en la dirección radial es
La ecuación del movimiento en la dirección tangencial es
La aceración tangencial at=α·xc, la aceleración normal an=ω2·xc. Despejamos las componentes Ft y Fn de la fuerza que ejerce el eje
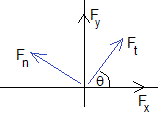
Alternativamente, el eje ejerce dos fuerzas, mutuamente perpendiculares, Fx y Fy que están relacionadas con Ft y Fn, de la siguiente forma
Práctica de laboratorio
En el laboartorio disponemos de los tres cuerpos que se muestran en la fotografía
- Disco de m=89 g de masa y 8 cm de diámetro
- Un disco de 102 g de masa y 9.6 cm de diámetro, con un hueco circular de 4.3 cm de diámetro.
- Una varilla de 38 cm de longitud, 28 g de masa, tiene un cilindro deslizante de 2.5 cm de diámetro, 2 cm de longitud y 75 g de masa situado a una distancia d=25 cm del eje que pasa por O, estando O a 2.5 cm del extremos de la varilla, tal como se muestra en la figura
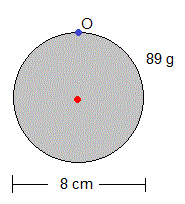
Calculamos el momento de inercia respecto de un eje perpendicular al plano del disco y que pasa por el punto O
El centro de masas está en el centro del disco, a 4 cm del eje que pasa por O
x1=4 cm
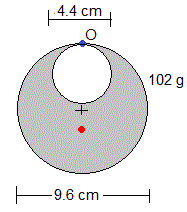
Calculamos la masa M del disco sin el hueco, suponiendo que es uniforme y de espesor constante
La masa del hueco m=129.1-102=27.1 g
Calculamos el momento de inercia respecto de un eje perpendicular al plano del disco y que pasa por el punto O
Calculamos la posición del centro de masas respecto de O
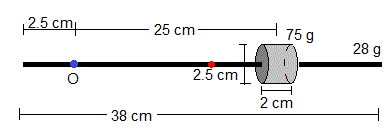
Calculamos el momento de inercia respecto de un eje perpendicular a la varilla y que pasa por el punto O
Calculamos la posición del centro de masas respecto de O
El programa CAPSTONE de PASCO, representa los datos proporcionados por el sensor de movimiento de rotación
Desviamos uno de los cuerpos, el disco con un hueco, de la posición de equilibrio un ángulo θ0 y lo soltamos.
En una gráfica de la posición angular θ en función del tiempo t, medimos con la herramienta delta el desplazamiento angular máximo 2θ0=3.585 rad
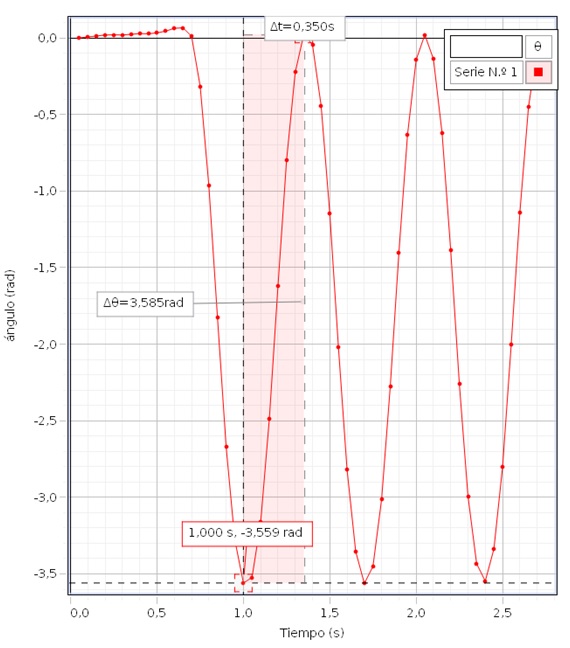
En una gráfica de la velocidad angular ω en función del tiempo t, medimos con la herramienta coordenadas la velocidad angular máxima, (cuando pasa por la posición de equilibrio θ=0), ωmáx=16.933 rad/s
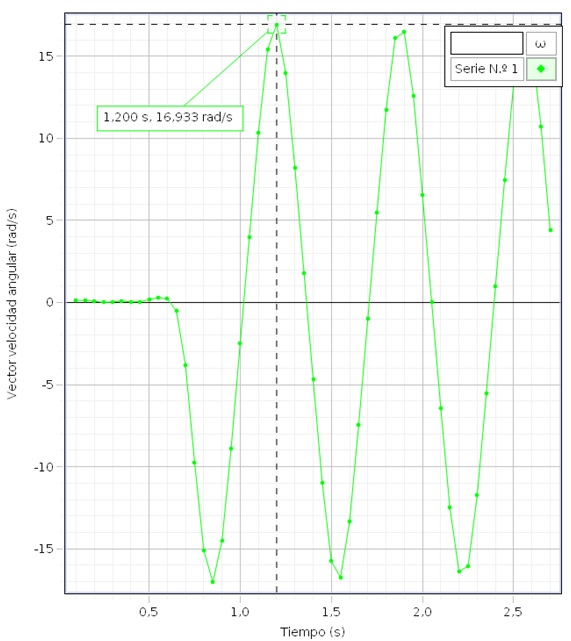
Con los datos correspondientes al disco con un hueco, calculamos la velocidad angular máxima para el ángulo θ0=1.7925 rad
Simulación
La ecuación de la dinámica de rotación es
Donde es el momento angular, y es el momento de las fuerzas externas que actúan sobre el sólido rígido
El momento del peso mg que actúa en el centro de masas distante xcm del eje O de rotación es -mgd=-mgxcmsinθ
Resolvemos esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=θ0, y dθ/dt=0. Se desvía un ángulo θ0 de la posición de equilibrio estable y se suelta.
I=4.266e-4; %momento de inercia del disco con hueco
x_cm=0.0549; %posición del c.m.
m=0.102; %masa
th_0=1.7925; %ángulo de desviación
f=@(t,x)[x(2); -m*9.8*x_cm*sin(x(1))/I];
opts=odeset('events',@rotacion_ode45);
[t,x]=ode45(f,[0,10],[th_0,0],opts);
plot(x(:,1),x(:,2))
grid on
xlabel('\theta')
ylabel('\omega');
title('Conservación de la energía')
Representamos la velocidad angular ω en función de la posición angular θ. Detenemos el proceso de integración cuando el sólido pasa por la posición de equilibrio θ=0, definiendo la función rotacion_ode45
function [detect,stopin,direction]=rotacion_ode45(~,x)
detect=x(1);
stopin=1;
direction=-1;
end
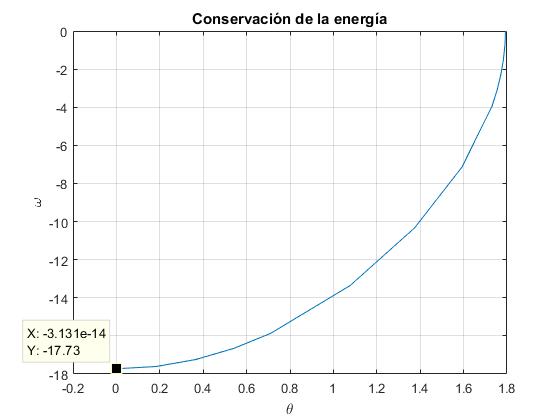
La velocidad angular máxima para θ=0, es 17.73 rad/s
Actividades
Se selecciona el cuerpo:
- Un disco
- Un disco con un hueco
- Una varilla con una masa cilíndrica deslizante. Cambiamos la posición del cilindro, en el control titulado Distancia cilindro
Se establece el ángulo de desviación en grados en el control titulado Angulo de desviación
Se pulsa el botón titulado Nuevo
En la parte superior izquierda, se proporcionan los datos del tiempo t, la posición angular θ en grados y la velocidad angular ω en rad/s
Con el botón paso a paso, >| se mide la velocidad angular máxima ω, cuando la posición angular θ=0.

