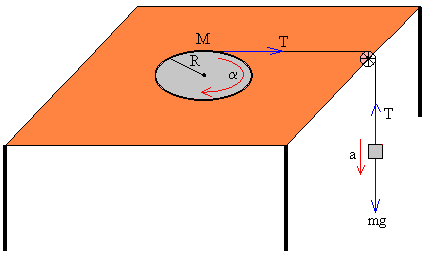
Un disco de masa M y radio R está situado encima de una mesa y puede girar alrededor de un eje vertical. Está conectado mediante una cuerda que pasa por una polea de masa despreciable a un bloque de masa m. A medida que el bloque desciende, la cuerda se desenrolla del borde del disco y lo hace girar alrededor de su eje. Vamos a calcular la aceleración a del bloque, sabiendo que el coeficiente de rozamiento entre el disco y el plano horizontal sobre el que está apoyado es μ.

Las fuerzas sobre el bloque son

• El peso mg
• La tensión de la cuerda T

Si el bloque se mueve con aceleración a, la ecuación del movimiento es

mg-T=ma

Aplicamos la ecuación de la dinámica de rotación al disco de masa M y radio R.

• La tensión de la cuerda ejerce un momento T·R

• El rozamiento entre la superficie del disco y el plano horizontal ejerce un momento M_r que se opone al movimiento de rotación del disco, y que calcularemos más adelante

Si el disco gira con aceleración angular α, la ecuación del movimiento es

T·R-M_r=I α

El momento de inercia del disco, respecto del eje vertical es MR²/2

Como la aceleración del bloque es la aceleración tangencial de un punto del borde del disco, la relación entre las dos aceleraciones es a= α·R

Eliminando la tensión T de la cuerda, despejamos la aceleración a del bloque

${\displaystyle a=\frac{2(mg-M_r/R)}{2m+M}}$

Momento de rozamiento

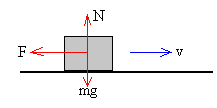
Cuando un bloque desliza sobre un plano horizontal, la fuerza de rozamiento se opone al desplazamiento, su valor es F_r= μ·N, donde N es la reacción del plano igual al peso del bloque.

Consideremos un disco en rotación con velocidad angular ω, apoyado en un plano horizontal. Tomamos un elemento del disco, a una distancia r de su centro. La velocidad de dicho elemento es ω·r, y su dirección es perpendicular al radio. La fuerza de rozamiento se opone al movimiento de dicho elemento, tal como se muestra en la figura.

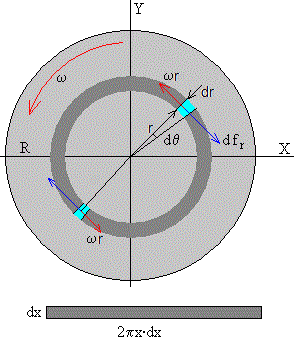
Si dividimos el disco en anillos de radio r, y de anchura dr, observamos que el momento de las fuerzas de rozamiento debidos a todos los elementos del anillo tiene el mismo módulo, la misma dirección y sentido. El momento resultante es

dM_r= μ·dN·r

donde dN es la reacción del plano igual al peso del anillo de radio r y espesor dr

${\displaystyle dN=\frac{Mg}{\pi R^2}2\pi r·dr=\frac{2Mg}{R^2}r·dr}$

El momento total, es la suma de los momentos de todos los anillos en los que hemos dividido el disco

${\displaystyle M_r={\displaystyle \underset{0}{\overset{R}{\int }}\mu \frac{2Mg}{R^2}{r}^{2}dr}=\frac{2\mu MgR}{3}}$

Introduciendo el valor de M_r en la fórmula de la aceleración a del bloque

${\displaystyle a=\frac{6m-4\mu M}{6m+3M}g}$

La velocidad del bloque cuando ha descendido una altura h partiendo del reposo, vale

${\displaystyle v=\sqrt{2ah}=\sqrt{2\frac{6m-4\mu M}{6m+3M}gh}}$

Balance energético

Cuando el bloque desciende una altura h, adquiere una velocidad v y el disco gira con velocidad angular ω, con v=ω·R.

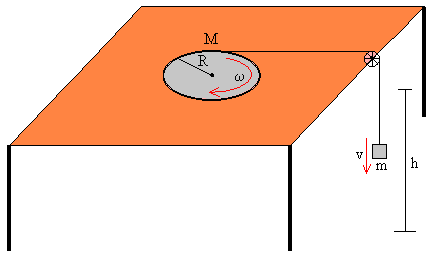
La energía potencial del bloque mgh se convertiría en energía cinética del bloque mv²/2  y del disco Iω²/2 si no hubiese rozamiento.

Una parte de la energía potencial se convierte en trabajo de la fuerza de rozamiento, que es el producto del momento de rozamiento M_r por el ángulo girado θ=h/R por el disco

W=-M_r·θ

El balance energético se expresa mediante la ecuación

${\displaystyle mgh-M_r\theta =\frac{1}{2}m{v}^2+\frac{1}{2}\left(\frac{1}{2}M{R}^2\right){\omega }^2}$

Despejamos la velocidad v del bloque

${\displaystyle v=\sqrt{\frac{12m-8\mu M}{6m+3M}gh}}$

Ejemplo

• Masa del disco M=1.0 kg
• Masa del bloque m=0.25 kg
• Coeficiente de rozamiento μ=0.3

La aceleración del bloque es

${\displaystyle a=\frac{6·0.25-4·0.3·1.0}{6·0.25+3·1.0}9.8=0.65{\text{m/s}}^{\text{2}}}$

Cuando el bloque desciende h=1 m partiendo del reposo, alcanza una velocidad de

${\displaystyle v=\sqrt{2·0.65·1.0}=1.14\text{m/s}}$

Actividades

Se introduce

• La masa del disco M, en el control titulado Masa disco
• La masa del bloque m, en el control titulado Masa bloque
• El coeficiente de rozamiento μ, en el control titulado Coeficiente rozamiento
• El radio del disco se ha fijado en el valor R=0.25 m

Se pulsa el botón titulado Nuevo

Si se cumple que 6m>4μM, la aceleración del bloque a>0. Observamos como el bloque desciende. En la parte superior izquierda, se muestra: el tiempo t, la posición del bloque x y su velocidad v.

En la parte central, un diagrama en forma de tarta nos muestra el balance energético:

• La energía potencial del bloque, en color azul;.
• La energía cinética del bloque, en color rojo.
• La energía cinética del disco, en color rosa.
• El trabajo de la fuerza de rozamiento, en color gris.

Problema

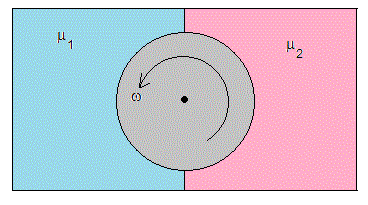
Una superficie horizontal está dividida en dos partes, que tienen diferente textura. Un disco de masa M y radio R se coloca sobre la superficie de modo que el centro del disco está en la línea que divide la superficie.

El coeficiente cinético entre el disco y la parte izquierda de la superficie es μ₁. El coeficiente cinético entre el disco y la parte derecha de la superficie es μ₂. Suponiendo que μ₁>μ₂.

Determinar la fuerza sobre el disco, cuando gira con velocidad angular ω

Consideremos un elemento diferencial de área del disco situando a una distancia r del centro y haciendo un ángulo θ con el eje X

Su posición y velocidad son

${\displaystyle \begin{array}{l}\overrightarrow{r}=r\cos \theta ·\widehat{i}+r\sin \theta ·\widehat{j}\\ \overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}=\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 0& 0& \omega \\ r\cos \theta & r\sin \theta & 0\end{array}\right|=\omega r\left(-\sin \theta ·\widehat{i}+\cos \theta ·\widehat{j}\right)\end{array}}$

Como puede apreciarse en la parte izquierda de la figura

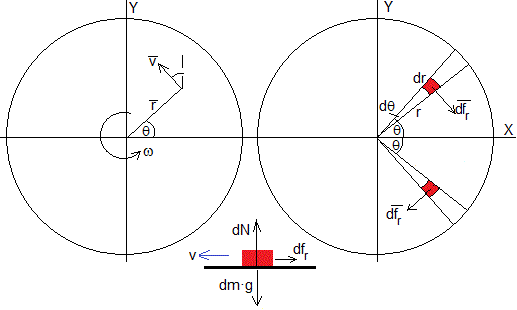
La fuerza de rozamiento sobre un elemento diferencial de área (en color rojo) del disco, comprendido entre r y r+dr y entre θ y θ+dθ, es de sentido contrario a la velocidad

${\displaystyle \overrightarrow{d{f}_r}=\mu dN\left(\sin \theta ·\widehat{i}-\cos \theta ·\widehat{j}\right)}$

dN es la normal, de sentido contrario al peso dm·g, del elemento diferencial del disco

En la parte derecha de la figura, vemos que por simetría, las componentes a lo largo de eje X de la fuerza de rozamiento se anulan de dos en dos. La dirección de la fuerza de rozamiento será el eje Y

${\displaystyle \begin{array}{l}dm=\frac{M}{\pi R^2}\left(rd\theta ·dr\right)\\ dN=\frac{Mg}{\pi R^2}\left(rd\theta ·dr\right)\\ \overrightarrow{d{f}_r}=\mu \frac{Mg}{\pi R^2}r\left(\sin \theta ·\widehat{i}-\cos \theta ·\widehat{j}\right)d\theta ·dr\end{array}}$

• Calculamos la fuerza que ejerce la parte derecha de la superficie

${\displaystyle \begin{array}{l}\overrightarrow{F_2}={\mu }_2\frac{Mg}{\pi R^2}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}{\displaystyle \underset{0}{\overset{r}{\int }}r\left(\sin \theta ·\widehat{i}-\cos \theta ·\widehat{j}\right)d\theta ·dr}}\\ \overrightarrow{F_2}={\mu }_2\frac{Mg}{\pi R^2}\frac{R^2}{2}{\left(-\cos \theta ·\widehat{i}-\sin \theta ·\widehat{j}\right)|}_{-\pi /2}^{\pi /2}=-{\mu }_2\frac{Mg}{\pi }\widehat{j}\end{array}}$

Confirmamos que la dirección de la fuerza de rozamiento es el eje Y

• Calculamos la fuerza que ejerce la parte izquierda

${\displaystyle \begin{array}{l}\overrightarrow{F_1}={\mu }_1\frac{Mg}{\pi R^2}{\displaystyle \underset{\pi /2}{\overset{3\pi /2}{\int }}{\displaystyle \underset{0}{\overset{r}{\int }}r\left(\sin \theta ·\widehat{i}-\cos \theta ·\widehat{j}\right)d\theta ·dr}}\\ \overrightarrow{F_1}={\mu }_1\frac{Mg}{\pi R^2}\frac{R^2}{2}{\left(-\cos \theta ·\widehat{i}-\sin \theta ·\widehat{j}\right)|}_{\pi /2}^{3\pi /2}={\mu }_1\frac{Mg}{\pi }\widehat{j}\end{array}}$

La fuerza de rozamiento resultante es

${\displaystyle \overrightarrow{F_1}+\overrightarrow{F_2}=\frac{Mg}{\pi }\left({\mu }_1-{\mu }_2\right)\widehat{j}}$

Si la superficie es homogénea, μ₁=μ₂, la fuerza resultante es nula

Referencias

Sherfinski J. A rotacional dynamics problem with friction and calculus. The Physics Teacher. Vol 39, March 2001, pp. 150-15

Physics Challenge for Teachers and Students. A D.J.’s Nightmare. Phys. Teach. 45, October 2007, pp. 455