Cinemática

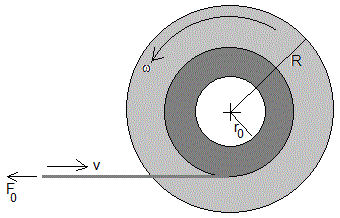
En los procesos de enrollado, se genera una espiral de Arquímedes de paso h constante

${\displaystyle r=r_0+\frac{h}{2\pi }\theta }$

La velocidad lineal en coordenadas polares es

${\displaystyle \begin{array}{l}{v}^2={\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\\ v^2={\left(\frac{dr}{d\theta }\right)}^2{\left(\frac{d\theta }{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\\ v=r\frac{d\theta }{dt}\sqrt{1+{\left(\frac{h}{2\pi r}\right)}^2}\end{array}}$

como h es pequeño frente a r

${\displaystyle v\approx r\frac{d\theta }{dt}\left(1+\frac{h^2}{8{\pi }^2{r}^2}+\mathrm{...}\right)\approx r\frac{d\theta }{dt}}$

Lo que equivale a despreciar la componente (dr/dt) radial de la velocidad

Los procesos de enrollado y desenrollado comparten estas características básicas: r=r₀+h·θ/(2π) con h muy pequeño frente a r y v≈r·dθ/dt

Si la velocidad v es constante, el radio r se incrementa con el tiempo t de la forma

${\displaystyle \begin{array}{l}v=r\frac{2\pi }{h}\frac{dr}{dt}\\ {\displaystyle \underset{r_0}{\overset{r}{\int }}r·dr=\frac{hv}{2\pi }t}\\ r^2=r_0^2+\frac{hv}{\pi }t\end{array}}$

Otra forma de escribir esta relación es la siguiente

${\displaystyle r^2=r_0^2\left(1+{\alpha }^2\frac{t}{T}\right),{\alpha }^2=\frac{R^2-r_0^2}{r_0^2}}$

El parámetro α², se mide en términos del radio inicial r₀ y del radio final R. T es el tiempo que tarda en pasar del primero al segundo.

Dinámica

Supongamos que la velocidad del hilo es v constante

A medida que se enrolla el hilo, la bobina incrementa su masa, dm=λv·dt, donde λ es la densidad lineal (masa por unidad de longitud)

La masa de la bobina en el instante t es m=m₀+dm=λ·vt. Supondremos que es despreciable la masa m₀ de la bobina sin hilo.

Si la masa total del hilo en la bobina es M, enrollada durante un tiempo T, en el tiempo t, la masa m del hilo en la bobina será, m=M·t/T

El hilo se enrolla en una bobina de radio interior r₀ y radio exterior r. El momento de de inercia de un cilindro hueco es

${\displaystyle \frac{1}{2}m\left(r_0^2+r^2\right)}$

El momento de inercia en el instante t será

${\displaystyle I(t)=I_0+\frac{1}{2}m(t)\left(r_0^2+r^2(t)\right)}$

El momento angular respecto del eje de rotación L=Iω=I·v/r

En la ecuación del movimiento se iguala la derivada con respecto del tiempo del momento angular L, con el momento de las fuerzas que actúan en el baobina:

• La tensión F₀ del hilo cuyo momento es, F₀r
• El par del motor, M_m
• El rozamiento en el eje, M_r

${\displaystyle \frac{dL}{dt}=M_m-F_{0}r-M_r}$

Supondremos que el rozamiento en el eje es despreciable, M_r=0. Derivamos el momemnto angular L con respecto del tiempo t y despejamos el par motor M_m

${\displaystyle \begin{array}{l}{M}_m=\left(F_0{r}_0+v\frac{M}{T}{r}_0\right)\sqrt{1+{\alpha }^2\frac{t}{T}}-\\ \left(I_0+M{r}_0^2\left(\frac{t}{T}\right)+\frac{1}{2}M{r}_0^2{\alpha }^2{\left(\frac{t}{T}\right)}^2\right)\frac{{\alpha }^2}{2T{r}_0{\left(1+{\alpha }^2\left(t/T\right)\right)}^{3/2}}\end{array}}$

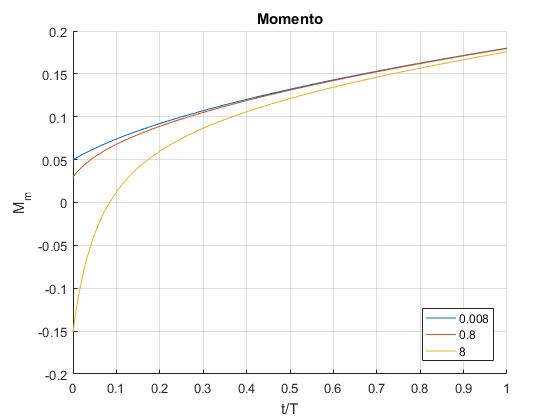
Representamos en el eje vertical el par motor, M_m, en el horizontal el cociente t/T, tomado los siguientes datos: velocidad constante del hilo v=1.0 m/s, masa del hilo enrollado M=3.0 kg, tensión del hilo F₀=2.0 N, radio de la bobina vacía, r₀=0.025 m, radio de la bobina con el hilo enrollado, R₀=0.090 m, tiempo total T=9500 s

r0=0.025; %radio inicial
R=0.09; %radio final
v=1; %velocidad constante del hilo
F0=2; %tensión hilo
M=3; %masa final de la bobina (del hilo enrollado)
T=9500; %tiempo total 
alfa2=(R^2-r0^2)/r0^2; %parámetro
hold on
for I0=[0.008,0.8,8] %momento de inercia sin bobina
    f=@(x) (F0*r0+v*M*r0/T)*sqrt(1+alfa2*x)-
(I0+M*r0^2*x+M*r0^2*alfa2*x.^2/2)*alfa2./(2*T*r0*(1+alfa2*x).^(3/2));
    fplot(f,[0,1],'displayName',num2str(I0))
end
hold off
legend('-DynamicLegend','location','southeast')
grid on
xlabel('t/T')
ylabel('M_m')
title('Momento')

Se ha representado el par motor para tres momento de inercia del dispositivo: I₀=0.008, I₀=0.8 y I₀=8 kgm²

La rueda de Maxwell

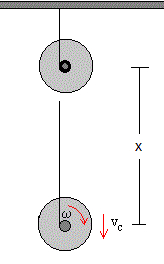
La rueda de Maxwell es un dispositivo que nos permite verificar la conservación de la energía mecánica: la energía potencial se transforma en energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle mgx=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2}$

En la página titulada La rueda de Maxwell la cuerda se suponía inextensible, de espesor nulo y de masa despreciable

Cuando el disco se deja caer una altura x, la velocidad v_c de traslación del centro del disco, se calcula aplicando el principio de conservación de la energía y teniendo en cuenta la relación entre el movimiento de traslación del c.m. y rotación del disco alrededor de un eje que pasa por el c.m., v_c=ωr₀. Siendo r₀ el radio del eje del disco, que no cambia cuando la cuerda se rolla, ya que suponemos que la cuerda es inextensible, tiene un espesor nulo y masa despreciable

${\displaystyle \begin{array}{l}mgx=\frac{1}{2}m{v}_c^2+\frac{1}{2}{I}_c{\left(\frac{v_c}{r_0}\right)}^2\\ v_c=\sqrt{\frac{2mgx}{m+\frac{I_c}{r_0^2}}}\end{array}}$

Si la cuerda tiene un anchura h pequeña, la relación v_c=ωr₀, no se mantiene ya que el radio disminuye desde r_m, cuando la cuerda está completamente enrollada, hasta r₀ cuando está desenrollada.

La cuerda de masa despreciable tiene espesor

Supondremos que la cuerda de masa desprecible, frente al disco, tiene un espesor h no nulo

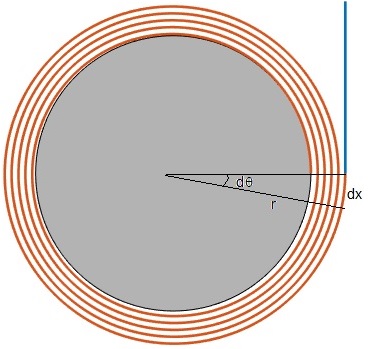
La relación entre el radio r y el ángulo θ es

${\displaystyle r=r_m-\frac{h}{2\pi }\theta }$

siendo h el espesor de la cuerda y r_m el radio incial del eje del disco con la cuerda enrollada

r0=1; 
h=0.05; 
ang=(1:360)*pi/180; %tronco
hold on
fill(r0*cos(ang),r0*sin(ang),[0.7 0.7 0.7])
r=@(x) r0+h*x/(2*pi);
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,10*pi], 'lineWidth',2)
line([r(10*pi),r(10*pi)],[0,r(10*pi)],'lineWidth',2)
hold off
axis off
axis equal

La figura muestra que un arco ds de cuerda se transforma en un desplazamiento dx del centro del disco.

En coordenadas polares el arco ds es

${\displaystyle \begin{array}{l}ds=\sqrt{{\left(dr\right)}^2+r^2{\left(d\theta \right)}^2}=\sqrt{{\left(-\frac{h}{2\pi }\right)}^2+{\left(r_m-\frac{h}{2\pi }\theta \right)}^2}d\theta \approx \left(r_m-\frac{h}{2\pi }\theta \right)d\theta \\ dx=\left(r_m-\frac{h}{2\pi }\theta \right)d\theta \end{array}}$

Integramos sabiendo que para θ=0, x=0.

${\displaystyle x=r_m\theta -\frac{h}{4\pi }{\theta }^2}$

Despejamos el ángulo θ

${\displaystyle \theta =\frac{2\pi }{h}\left(r_m-\sqrt{r_m^2-\frac{h}{\pi }x}\right)}$

Cuando x=d, la cuerda se ha desenrollado completamente, el ángulo máximo θ₀ es

${\displaystyle {\theta }_0=\frac{2\pi }{h}\left(r_m-\sqrt{r_m^2-\frac{h}{\pi }d}\right)}$

El radio mínimo del eje del disco será r₀, este es el radio que conocemos

${\displaystyle \begin{array}{l}{r}_0=r_m-\frac{h}{2\pi }{\theta }_0=\sqrt{r_m^2-\frac{h}{\pi }d}\\ r_m^2=r_0^2+\frac{h}{\pi }d\end{array}}$

El desplazamiento dx del centro del disco vale

${\displaystyle \begin{array}{l}dx=\left(r_m-\frac{h}{2\pi }\theta \right)d\theta \\ dx=\sqrt{r_m^2-\frac{h}{\pi }x}·d\theta \end{array}}$

La velocidad de traslación (dx/dt) y rotación (dθ/dt) dejan de ser proporcionales

${\displaystyle \frac{dx}{dt}=\sqrt{r_0^2+\frac{h}{\pi }(d-x)}·\frac{d\theta }{dt}}$

Llevando esta relación a la ecuación de la conservación de la energía

${\displaystyle \begin{array}{l}mgx=\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}\frac{I_c}{r_0^2+\frac{h}{\pi }(d-x)}{\left(\frac{dx}{dt}\right)}^2\\ \frac{dx}{dt}=\sqrt{\frac{2mgx}{m+\frac{I_c}{r_0^2+h(d-x)/\pi }}}\end{array}}$

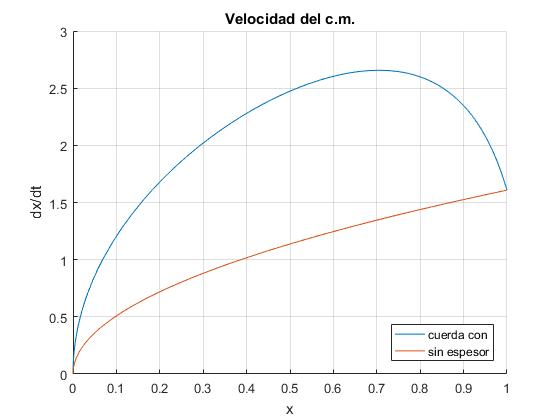
Representamos la velocidad de traslación dx/dt, suponiendo que la cuerda de masa despreciable tiene un espesor no nulo, junto con la gráfica de la velocidad de traslación v_c suponiendo un espesor nulo

Los datos tomados del artículo citado en las referencias son los siguientes: masa del disco, m=51.3 g, radio del eje del disco, r₀=4 mm, espesor de la cuerda h=1 mm, momento de inercia del disco I_c=5.4·10^-6 kgm², longitud de la cuerda d=1 m

rm=0.024; %radio 
Ic=5.4e-6; %momento de inercia
m=0.0513; %masa
h=0.001; %espesor hilo
d=1; %longitud cuerda
r0=0.004; %radio del eje (sin hilo)
hold on
f=@(x) sqrt(2*m*9.8*x./(m+Ic./(r0^2+h*(d-x)/pi))); 
g=@(x) sqrt(2*m*9.8*x/(m+Ic/r0^2));
fplot(f,[0,1])
fplot(g,[0,1])
hold off
grid on
legend('cuerda con','sin espesor', 'location','southeast')
xlabel('x')
ylabel('dx/dt')
title('Velocidad del c.m.')

Referencias

J. P. McKelvey. General kinematics of winding processes. Am. J. Phys. 53 (12) December 1985, pp. 1156-1159

J. P. McKelvey. Dynamics and kinematics of textile machinery Am. J. Phys. 50(12) December 1982, pp. 1160-1162

Ultimo apartado

Charles de Izarra. Mechanical study of a modern yo-yo. Eur. J. Phys. 32 (2011) pp. 1097-1106