La rueda dentada

Dibujamos una rueda dentada de N=6 y 12 dientes, de radio R=1 y de radio interior r.

N=12;
R=1; %radio
r=0.575; %radio interior
x=zeros(1,2*N)
y=zeros(1,2*N)
for i=1:2:2*N
    x(i)=R*cos((i-1)*pi/N);
    y(i)=R*sin((i-1)*pi/N);
    x(i+1)=r*cos((i-1)*pi/N+pi/N);
    y(i+1)=r*sin((i-1)*pi/N+pi/N);
end
x=[x,R];
y=[y,0];
hold on
fill(x,y,'c')
plot(0,0,'o','markersize',3,'markeredgecolor','k','markerfacecolor','k')
plot(x,y,'k')
hold off
axis equal
axis off

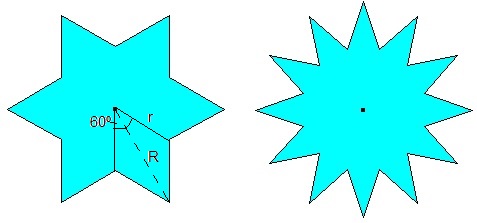
En el caso de una típica estrella de seis puntas, hay una relación sencilla entre r y R, rcos30=R/2, $r=R/\sqrt{3}$

Momento de inercia de la rueda dentada respecto de un eje que pasa por el c.m.

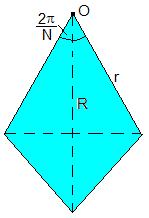
Supondremos una rueda dentada de forma cilíndica de longitud L y masa M

Consideremos la porción de rueda cuya sección se muestra en la figura. Calculamos el momento de inercia respecto a un eje perpendicular al plano de la figura que pasa por O y la multiplicamos por el número de dientes, N.

La densidad ρ del material es el cociente entre la masa M de la rueda y su volumen, N veces el volumen de la porción cuya sección se muestra en la figura.

El área del triángulo superior es r·sin(π/N)cos(π/N), el área del triángulo inferior es r·sin(π/N)(R-rcos(π/N)), el área total es rR·sin(π/N). El volumen de la porción de rueda L·Rr·sin(π/N), y el volumen de la rueda N·LRr·sin(π/N), la densidad

${\displaystyle \rho =\frac{M}{NLRr\cos \left(\frac{\pi }{N}\right)}}$

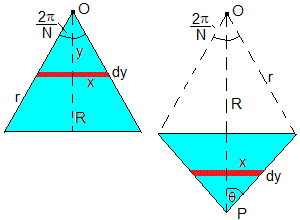
El momento de inercia respecto a un eje perpendicular al plano de la figura que pasa por O, de la porción triangular superior es

${\displaystyle \begin{array}{l}{I}_1=\rho L{\displaystyle \underset{0}{\overset{r\cos \left(\frac{\pi }{N}\right)}{\int }}{y}^2(2x·dy)}=2\rho L\tan \left(\frac{\pi }{N}\right){\displaystyle \underset{0}{\overset{r\cos \left(\frac{\pi }{N}\right)}{\int }}{y}^{3}dy}\\ =\frac{1}{2}\rho L{r}^4\tan \left(\frac{\pi }{N}\right){\cos }^4\left(\frac{\pi }{N}\right)\end{array}}$

El momento de inercia de la porción triangular inferior respecto al mismo eje que pasa por O, se calcula de forma similar. El ángulo θ vale

${\displaystyle \tan \theta =\frac{r\sin \left(\frac{\pi }{N}\right)}{R-r\cos \left(\frac{\pi }{N}\right)}}$

El momento de inercia es

${\displaystyle \begin{array}{l}{I}_2=\rho L{\displaystyle \underset{r\cos \left(\frac{\pi }{N}\right)}{\overset{R}{\int }}{y}^2(2x·dy)}=2\rho L\tan \theta {\displaystyle \underset{r\cos \left(\frac{\pi }{N}\right)}{\overset{R}{\int }}{y}^{3}dy}=\\ 2\rho L\tan \theta \left(\frac{R^4}{12}-R\frac{r^3{\cos }^3\left(\frac{\pi }{N}\right)}{3}+\frac{r^4{\cos }^4\left(\frac{\pi }{N}\right)}{4}\right)\end{array}}$

El momento de inercia total respecto del eje perpendicular al plano de la figura que pasa por O, es

${\displaystyle I_{cm}=I_1+I_2=\frac{M}{R}\left\{\frac{1}{2}{r}^3{\cos }^3\left(\frac{\pi }{N}\right)+\frac{2}{R-r\cos \left(\frac{\pi }{N}\right)}\left(\frac{R^4}{12}-R\frac{r^3{\cos }^3\left(\frac{\pi }{N}\right)}{3}+\frac{r^4{\cos }^4\left(\frac{\pi }{N}\right)}{4}\right)\right\}}$

El momento de inercia respecto de un eje paralelo que pasa por el vértice P se obtiene aplicando el teorema de Steiner

Cuando N→∞, r→R entonces I_cm→MR²/2, que es momento de inercia de un cilindro de masa M y radio R respecto de su eje

Conservación de la energía

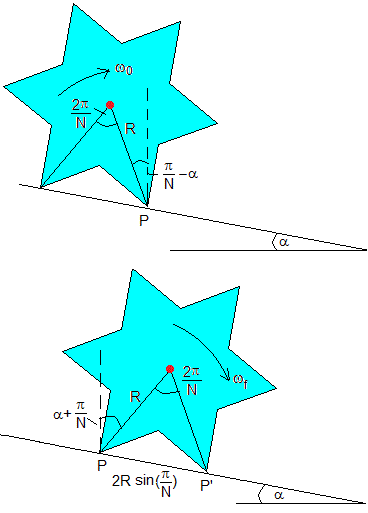
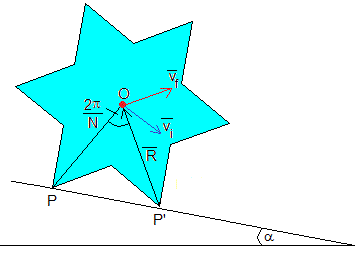
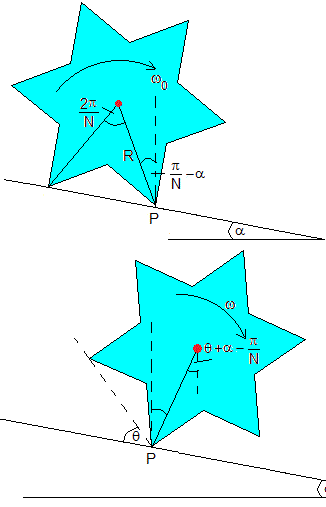
Vamos a estudiar el movimiento de la rueda dentada de masa M, radio R, situado sobre un plano inclinado α. La rueda gira alrededor de un eje perpendicular al plano de la figura que pasa por el vértice P. El c.m. del lápiz (punto de color rojo) describe un arco de circunferencia de radio R y ángulo 2π/N. En la parte superior de la figura, se muestra la situación inicial, la velocidad angular inicial es ω₀

La energía de la rueda dentada en la posición inicial es la suma de la energía cinética de rotación alrededor del eje que pasa por el vértice P y la energía potencial del centro de masa, que está a una altura Rcos(π/N-α) sobre P, tal como vemos en la figura.

${\displaystyle E=\frac{1}{2}I{\omega }_0^2+mgR\cos \left(\frac{\pi }{N}-\alpha \right)}$

En la parte inferior de la figura, se muestra la rueda en la situación final, cuando ha completado un giro de 2π/N alrededor del eje que pasa por el vértice P. La velocidad angular de rotación es ω_f y el centro de la rueda está a una altura Rcos(π/N+α) sobre P. Después del choque del vértice P' con el plano inclinado, el nuevo eje de rotación pasa por dicho vértice P' distante 2Rsin(π/N) de P

${\displaystyle E=\frac{1}{2}I{\omega }_f^2+mgR\cos \left(\frac{\pi }{N}+\alpha \right)}$

Conocida la velocidad angular inicial ω₀, calculamos la velocidad angular final ω_f, aplicando el principio de conservación de la energía

${\displaystyle \frac{1}{2}I{\omega }_0^2+2MgR\sin \left(\frac{\pi }{N}\right)\sin \alpha =\frac{1}{2}I{\omega }_f^2}$

Para obtener este resultado utilizamos la relación trigonométrica, cos(A-B)-cos(A+B)=2sinA·sinB. Con A=π/N y B=α.

Choque de un vértice con el plano inclinado

En la página titulada Una caja que puede volcar, una caja que desliza sin rozamiento a lo largo de un plano horizontal, choca con un obstáculo puntual. Se aplica el principio de conservación del momento angular, para calcular la velocidad angular de rotación de la caja después del choque. Aquí aplicamos el mismo principio.

La rueda gira alrededor del eje perpendicular al plano de la figura que pasa por P, hasta que el vértice siguiente, entra en contacto con el plano inclinado en P', en ese momento, la velocidad del c.m. v_i=ω_f y es perpendicular al radio vector PO. Inmediatamente después del choque, el eje de rotación pasa de P a P' y la velocidad después del choque es v_f perpendicular al radio vector P'O.

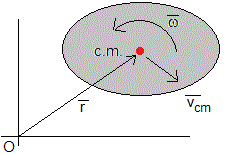
El momento angular respecto de O de un sólido rígido de masa M cuyo c.m. se traslada con velocidad $\overrightarrow{v_{cm}}$, y gira alrededor de un eje que pasa por el c.m. con velocidad angular $\overrightarrow{\omega }$, es

${\displaystyle \overrightarrow{L}=I_{cm}\overrightarrow{\omega }+m\overrightarrow{r}\times \overrightarrow{v_{cm}}}$

El momento angular inicial respecto del eje que pasa por P' es

${\displaystyle \begin{array}{l}L=I_{cm}{\omega }_f+MR{v}_i\sin \left(\frac{\pi }{2}+\frac{2\pi }{N}\right)=I_{cm}{\omega }_f+M{R}^2{\omega }_f\cos \left(\frac{2\pi }{N}\right)=\\ \left(I_{cm}+M{R}^2-2M{R}^2{\sin }^2\left(\frac{\pi }{N}\right)\right){\omega }_f\end{array}}$

siendo ω_f la velocidad angular de rotación final justo antes del choque. Se ha utilizado la relación trigonométrica cos(2A)=cos²A-sin²A

El momento angular final es de un sólido que gira alrededor del eje que pasa por P' con velocidad angular ω₀, la inicial para la siguiente etapa del movimiento

${\displaystyle L=I{\omega }_0=\left(I_{cm}+M{R}^2\right){\omega }_0}$

Aplicamos la conservación del momento angular, y despejamos la velocidad angular final ω₀

${\displaystyle \begin{array}{l}{\omega }_0=\left(1-\frac{2}{1+\frac{I_{cm}}{M{R}^2}}{\sin }^2\left(\frac{\pi }{N}\right)\right){\omega }_f\\ {\omega }_0=k{\omega }_f\end{array}}$

Etapas del movimiento de la rueda dentada

El movimiento de la rueda dentada consta por tanto, de dos etapas:

• Movimiento de rotación de 2pi/N alrededor de un eje fijo que pasa por el vértice situado en P

Conocida la velocidad angular inicial ω₀, calculamos la velocidad angular final ω_f, aplicando el principio de conservación de la energía

${\displaystyle \frac{1}{2}I{\omega }_0^2+2MgR\sin \left(\frac{\pi }{N}\right)\sin \alpha =\frac{1}{2}I{\omega }_f^2}$

• Choque del vértice con el plano inclinado

La velocidad angular inicial ω₀ para la siguiente rotación alrededor de un eje que pasa por P', se calcula mediante la conservación del momento angular

${\displaystyle {\omega }_0=k{\omega }_f}$

• Etapas del movimiento:

• Etapa inicial



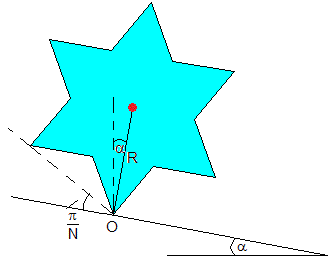
Establecemos como situación inicial aquella en el que la rueda dentada se ha girado θ=π/N, tal como se muestra en la figura y se suelta, la velocidad angular inicial es cero. La rueda empieza su movimiento a lo largo del plano inclinado. Su velocidad angular final justo antes de que el siguiente vértice entre en contacto con el plano inclinado, es

${\displaystyle MgR\cos \alpha =\frac{1}{2}I{\omega }_f^2+MgR\cos \left(\frac{\pi }{N}+\alpha \right)}$

• Primera etapa

La velocidad al comienzo de la primera etapa es, ω₀=k·ω_f

La velocidad final al terminar la primera etapa es ω_f que se calcula aplicando el principio de conservación de la energía

${\displaystyle \frac{1}{2}I{\omega }_0^2+2MgR\sin \left(\frac{\pi }{N}\right)\sin \alpha =\frac{1}{2}I{\omega }_f^2}$

• Segunda etapa

La velocidad al comienzo de la segunda etapa es, ω₀=k·ω_f

y así, sucesivamente...

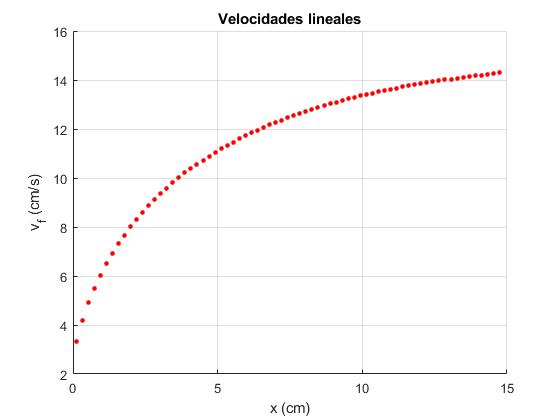
Calculamos las velocidades del centro de la rueda justo antes de que el vértice de la rueda entre en contacto el plano inclinado en función de la posición del vértice en dicho plano

• Número de dientes, N=12
• Radio de la rueda, R=1 cm
• Radio interior, r=0.575 cm
• La masa M no afecta al movimiento de la rueda
• El ángulo del plano inclinado, α=1.39°

N=12; %número de dientes
R=1/100; %radio, 
r=0.575/100; %radio interior, 
M=1; % masa no afecta
alfa=1.39*pi/180; %plano inclinado
I_cm=M*((r*cos(pi/N))^3/2+2*(R^4/12-R*(r*cos(pi/N))^3/3+
(r*cos(pi/N))^4/4)/(R-r*cos(pi/N)))/R;
I=I_cm+M*R^2; %momento de inercia respecto de un eje que pasa por el vértice
k=1-2*sin(pi/N)^2/(1+I_cm/(M*R^2));
wf=sqrt(M*9.8*R*(cos(alfa)-cos(pi/N+alfa))*2/I); %etapa inicial
hold on
plot(R*sin(pi/N)*100,wf*R*100,'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
for i=1:30
    w0=k*wf;
    wf=sqrt((I*w0^2/2+2*M*9.8*R*sin(pi/N)*sin(alfa))*2/I);
    h=(2*i+1)*R*sin(pi/N)*100;
    plot(h,wf*R*100,'o','markersize',3,'markeredgecolor','r',
'markerfacecolor','r')
end
grid on
xlabel('x (cm)')
ylabel('v_f (cm/s)')
title('Velocidades lineales')



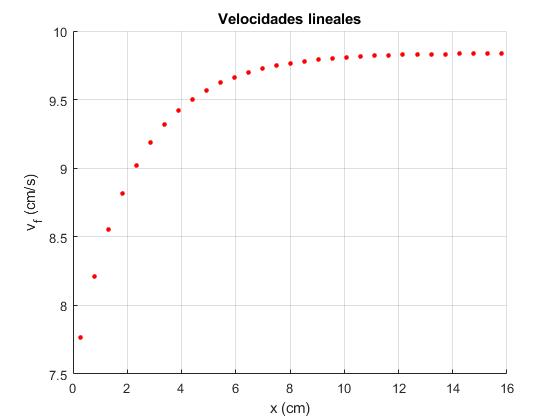
La velocidad parece tender hacia un valor límite constante

Si incrementamos el número de dientes N, la velocidad tiende a crecer linealmente con el tiempo, como un cilindro que rueda sin deslizar a lo largo de un plano inclinado

N=30; %número de dientes
R=1/100; %radio, 
r=0.845/100; %radio interior,
...

Tiempo entre dos choques

La rueda dentada que parte con velocidad ω₀, cuando ha girado un ángulo θ ha empleado un tiempo t, su velocidad angular es dθ/dt. Aplicamos el principio de conservación de la energía

${\displaystyle \begin{array}{l}{E}_0=\frac{1}{2}I{\left(\frac{d\theta }{dt}\right)}^2+MgR\cos \left(\theta -\frac{\pi }{N}+\alpha \right)\\ t=\sqrt{\frac{I}{2E_0}}{\displaystyle \underset{0}{\overset{\frac{2\pi }{N}}{\int }}\frac{d\theta }{\sqrt{1-\frac{MgR}{E_0}\cos \left(\theta -\frac{\pi }{N}+\alpha \right)}}}\end{array}}$

Donde E₀ es la energía en el punto de partida

Normalmente, parte de la posición angular θ=0, con velocidad angular ω₀

${\displaystyle E_0=\frac{1}{2}I{\omega }_0^2+MgR\cos \left(\frac{\pi }{N}-\alpha \right)}$

En la situación inicial, el punto de partida es θ=π/N en reposo

${\displaystyle E_0=MgR\cos \alpha }$

y los límites de integración son, π/N y 2π/N

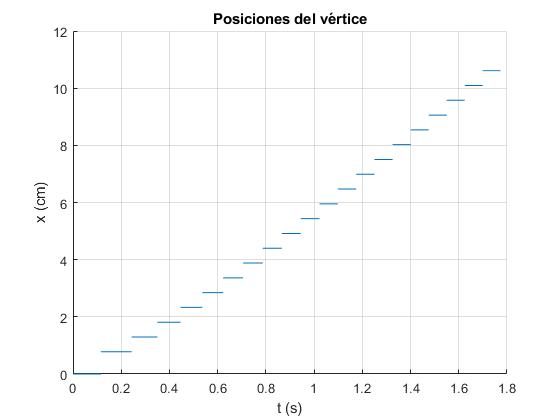
La rueda parte de la posición inicial en el origen, su energía E₀ es la potencial. Gira alrededor de un eje que pasa por el vértice inferior durante un tiempo t₀ que calculamos numéricamente resolviendo la integral definida entre los limites π/N y 2π/N. En el instante t₀ el siguiente vértice entra en contacto con el plano inclinado, el segundo eje de giro se encuentra en la posición Rsin(π/N).

Se calcula la velocidad ω_f justamente antes del choque, aplicando el principio de conservación de la energía, la velocidad inicial ω₀, justamente después del choque y su energía E₀ que se conserva durante la primera etapa del movimiento, hasta el próximo choque del siguiente vértice con el plano inclinado. Se calcula el tiempo t₁ que el segundo vértice está en contacto con el plano inclinado en la posición Rsin(π/N), resolviendo la integral definida entre los límites 0 y 2π/N.

La segunda etapa del movimiento comienza en el instante t₀+t₁ con el eje en la posición Rsin(π/N)+2Rsin(π/N). El movimiento se repite

Elaboramos un script, para representar la posición del eje de giro en función del tiempo

N=12;%número de dientes
R=1/100; %radio, cm
r=0.575/100; %radio interior, cm
M=1; % masa no afecta
alfa=1.39*pi/180; %plano inclinado
I_cm=M*((r*cos(pi/N))^3/2+2*(R^4/12-R*(r*cos(pi/N))^3/3+
(r*cos(pi/N))^4/4)/(R-r*cos(pi/N)))/R;
I=I_cm+M*R^2; %momento de inercia respecto de un eje que pasa por el vértice
k=1-2*sin(pi/N)^2/(1+I_cm/(M*R^2));
E0=M*9.8*R*cos(alfa); %situación inicial
f=@(x) 1./sqrt(1-M*9.8*R*cos(x-pi/N+alfa)/E0);
t=sqrt(I/(2*E0))*integral(f,pi/N, 2*pi/N);
wf=sqrt(M*9.8*R*(cos(alfa)-cos(pi/N+alfa))*2/I);

hold on
line([0,t],[0,0])
for i=1:20
    w0=k*wf;
    E0=I*w0^2/2+M*9.8*R*cos(pi/N-alfa);
    f=@(x) 1./sqrt(1-M*9.8*R*cos(x-pi/N+alfa)/E0);
    t1=sqrt(I/(2*E0))*integral(f,0, 2*pi/N);
    wf=sqrt((I*w0^2/2+2*M*9.8*R*sin(pi/N)*sin(alfa))*2/I);
    h=(2*i+1)*R*sin(pi/N)*100;
    line([t,t+t1],[h,h])
    t=t+t1;
end
grid on
xlabel('t (s)')
ylabel('x (cm)')
title('Posiciones del vértice')

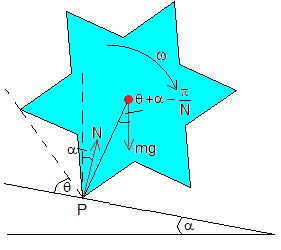
Ecuación del movimiento

Las fuerzas que actúan sobre la rueda son:

• El peso, mg
• la reacción N del plano inclinado, perpendicular al plano en el punto de contacto

La ecuación de la dinámica de rotación alrededor del eje que pasa por el vértice

${\displaystyle \left(I_{cm}+M{R}^2\right)\frac{d^2\theta }{d{t}^2}=MgR\sin \left(\theta +\alpha -\frac{\pi }{N}\right)}$

Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales:

• Situación inicial, parte de θ=π/N con velocidad angular (dθ/dt)₀=0.

Llega a la posición θ=2π/N con velocidad angular ω_f

Se produce el choque del vértice con el plano inclinado y se reduce la velocidad angular ω₀=k·ω_f,

• La condición inicial para la primera etapa del movimiento es, θ=0, (dθ/dt)₀=ω₀

y asi, sucesivamente

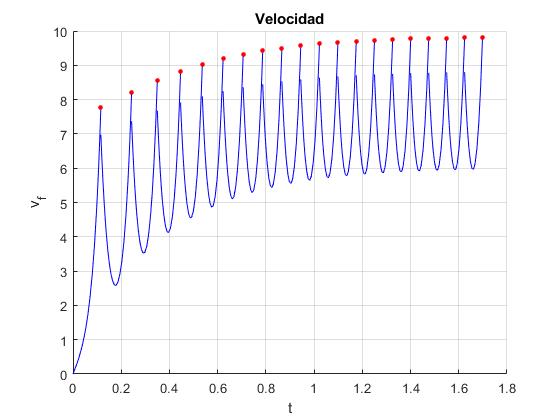
Elaboramos un script para respresentar la velocidad del centro de la rueda en función del tiempo, se señalan mediante puntos de color rojo, las velocidades finales ω_f, justamente antes de producirse el choque de un vértice con el plano inclinado

N=12;%número de dientes
R=1/100; %radio, cm
r=0.575/100; %radio interior, cm
M=1;  % masa no afecta
alfa=1.39*pi/180; %plano inclinado
I_cm=M*((r*cos(pi/N))^3/2+2*(R^4/12-R*(r*cos(pi/N))^3/3
+(r*cos(pi/N))^4/4)/(R-r*cos(pi/N)))/R;
I=I_cm+M*R^2; %momento de inercia respecto de un eje que pasa por el vértice
k=1-2*sin(pi/N)^2/(1+I_cm/(M*R^2));

v=zeros(1,20);
tf=zeros(1,20);
f=@(t,x) [x(2);M*9.8*R*sin(x(1)+alfa-pi/N)/I]; 
opts=odeset('events',@(t,x) estrella_ode45(t,x,N));
tt=0;
hold on
x0=[pi/N,0]; %condiciones iniciales, etapa inicial
for i=1:20
    [t,x,te,xe,ie]=ode45(f,[0,10],x0, opts);
    plot(tt+t,x(:,2)*R*100,'b') %velocidad angular
    tf(i)=t(end)+tt;
    tt=tt+te;
    v(i)=xe(2);  %antes del choque
    x0=[0, k*xe(2)]; %condiciones iniciales,
end
plot(tf,v*R*100, 'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
grid on
xlabel('t')
ylabel('v_f')
title('Velocidad')

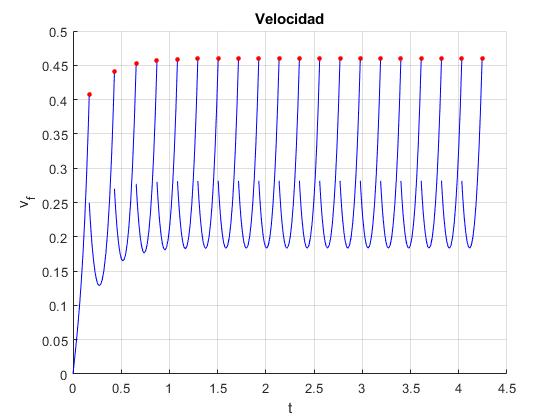
Cambiamos los datos para repetir con MATLAB, los cálculos realizados con el programa interactivo, más abajo

• El ángulo α del plano inclinado, α=10°
• El número de dientes, N=6
• El radio interior de la rueda dentada, $r=R/\sqrt{3}$

N=6; %número de dientes
R=0.05; %radio, cm
r=R/sqrt(3); %radio interior, cm
M=1; % masa no afecta
alfa=10*pi/180; %plano inclinado
....

Actividades

Se introduce

• El ángulo α del plano inclinado, en el control titulado Angulo α
• El número de dientes se ha fijado en N=6
• El radio de la rueda dentada se ha fijado en R=5 cm
• El radio interior de la rueda dentada se ha fijado $r=R/\sqrt{3}$
• La masa del lápiz se ha fijado en M=1

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la rueda dentada y la representación de la velocidad final de rotación ω_f, justamente antes del choque de un vértice con el plano inclinado. En el eje horizontal tenemos la posición del eje de rotación P.

Referencias

Lawrence R. Mead, Frank W. Bentrem. Almost rolling motion: An investigation of rolling grooved cylinders. Am. J. Phys. 66 (3) March 1998, pp. 202-208