En la página titulada, Escalera apoyada en dos paredes perpendiculares, se estudia el movimiento de una escalera cuyos extremos se apoyan en dos superficies lisas. El movimiento de la escalera desde la posición inicial hasta que impacta con el plano horizontal, se divide en dos etapas

• Mientras el extremo superior de la escalera está apoyado en la pared
• El extremo superior de la escalera deja de estar en contacto con la pared.

El ángulo crítico, que forma la escalera con la vertical, es

${\displaystyle {\theta }_l=\arccos \left(\frac{2}{3}\cos {\theta }_0\right)}$

Donde θ₀ es el ángulo inicial de partida en reposo

Consideremos una pared móvil de masa M situada en el origen y una escalera de masa m y longitud 2l apoyada en en suelo y en la pared tal como se muestra en la figura, cuando el ángulo que forma la escalera con la vertical es θ₀. Supondremos que las superficies sobre las que deslizan los extremos de la escalera son lisas (sin rozamiento). Se suelta la escalera, sus extremos empiezan a deslizar hasta que llega al suelo. Vamos a estudiar el movimiento de los dos cuerpos que forman este sistema aislado.

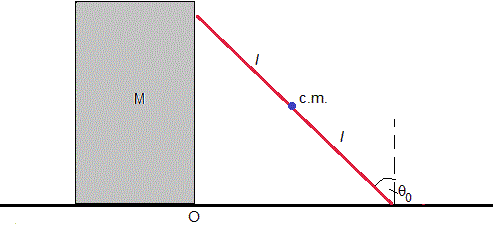
La escalera está apoyada en la pared móvil

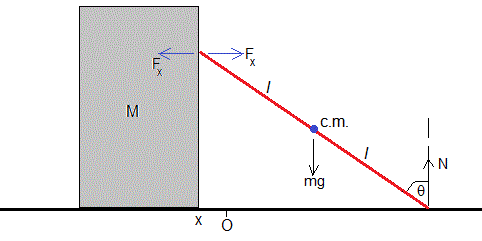
En el instante t, la posición de la pared es x, la posición del centro de masas de la escalera es

${\displaystyle \overrightarrow{r}\{\begin{array}{l}{x}_c=x+l\sin \theta \\ y_c=l\cos \theta \end{array}\overrightarrow{v}\{\begin{array}{l}\frac{d{x}_c}{dt}=\frac{dx}{dt}+l\cos \theta \frac{d\theta }{dt}\\ \frac{d{y}_c}{dt}=-l\sin \theta \frac{d\theta }{dt}\end{array}}$

Donde θ es el ángulo que forma la escalera con la vertical

La energía cinética de la pared es

${\displaystyle E_{k1}=\frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2}$

La energía cinética de la escalera es la suma de la energía cinética de traslación del c.m. (centro de masas) y de la energía cinética de rotación alrededor de un eje perpendicular que pasa por el c.m.

${\displaystyle \begin{array}{l}{E}_{k2}=\frac{1}{2}m\left\{{\left(\frac{d{x}_c}{dt}\right)}^2+{\left(\frac{d{y}_c}{dt}\right)}^2\right\}+\frac{1}{2}\left(\frac{1}{3}m{l}^2\right){\left(\frac{d\theta }{dt}\right)}^2=\\ \frac{1}{2}m\left\{{\left(\frac{dx}{dt}\right)}^2+2l\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}\right\}+\frac{2}{3}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

El momento de inercia de la escalera de masa m y longitud 2l respecto de un eje perpendicular que pasa por el c. m. es m(2l)²/12=ml²/3

La pared se mueve en el plano horizontal, su energía potencial no cambia. La energía potencial del c.m. de la escalera es E_p=mglcosθ.

La lagrangiana L=E_k1+E_k2-E_p es

${\displaystyle L=\frac{1}{2}(m+M){\left(\frac{dx}{dt}\right)}^2+ml\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}+\frac{2}{3}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2-mgl\cos \theta }$

La lagrangiana no depende de x, por lo que hay una constante del movimiento que denominamos P

${\displaystyle \begin{array}{l}\frac{\partial L}{\partial \dot{x}}=\text{cte}\\ (m+M)\frac{dx}{dt}+ml\cos \theta \frac{d\theta }{dt}=P\end{array}}$

Integramos, para obtener la posición de la pared móvil x en función del tiempo t y de la posición angular θ

${\displaystyle \begin{array}{l}x=\frac{P}{m+M}t-\frac{ml}{m+M}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\cos \theta ·d\theta }\\ x=\frac{P}{m+M}t-\frac{ml}{m+M}\left(\sin \theta -\sin {\theta }_0\right)\end{array}}$

Como es un sistema aislado, la energía se mantiene constante

${\displaystyle \begin{array}{l}E=\frac{1}{2}(m+M){\left(\frac{dx}{dt}\right)}^2+ml\cos \theta \frac{dx}{dt}\frac{d\theta }{dt}+\frac{2}{3}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta \\ E=\frac{1}{2}(m+M){\left\{\frac{1}{m+M}\left(P-ml\cos \theta \frac{d\theta }{dt}\right)\right\}}^2+ml\cos \theta \left\{\frac{1}{m+M}\left(P-ml\cos \theta \frac{d\theta }{dt}\right)\right\}\frac{d\theta }{dt}+\frac{2}{3}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta \\ E=\frac{P^2}{2(m+M)}+\left(\frac{2}{3}-\frac{m{\cos }^2\theta }{2(m+M)}\right)m{l}^2{\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta \end{array}}$

Expresamos la lagrangiana en términos del ángulo θ, del mismo modo que la energía

${\displaystyle L=\frac{P^2}{2(m+M)}+\left(\frac{2}{3}-\frac{m{\cos }^2\theta }{2(m+M)}\right)m{l}^2{\left(\frac{d\theta }{dt}\right)}^2-mgl\cos \theta }$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \left(\frac{4}{3}-\frac{m}{m+M}{\cos }^2\theta \right)l\frac{d^2\theta }{d{t}^2}+\frac{m}{m+M}l\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2-g\sin \theta =0\end{array}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la escalera está inclinada un ángulo θ₀ y se suelta, (dθ/dt)₀=0. La pared móvil está situada en el origen en reposo, x=0, dx/dt=0.

Estas condiciones iniciales hacen que la constante P=0 y la energía inicial E=mglcosθ₀

Fuerza de interacción

La escalera ejerce una fuerza F_x sobre la pared móvil que hace que se mueva hacia la izquierda

${\displaystyle F_x=M\frac{d^{2}x}{d{t}^2}=\frac{Mm}{m+M}l\left(\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-\cos \theta \frac{d^2\theta }{d{t}^2}\right)}$

Situación límite

La escalera va cayendo, deslizando su extemo superior por la pared móvil hasta que dejan de estar en contacto, en ese momento t_l, la fuerza F_x=0, la aceleración de la pared es nula. A partir de ese instante, la pared móvil y el c.m. de la escalera se mueven con velocidad constante

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{\sin \theta }{\cos \theta }{\left(\frac{d\theta }{dt}\right)}^2}$

Sustituyendo en la ecuación del movimiento, obtenemos la velocidad angular en el instante t_l

${\displaystyle \begin{array}{l}\left(\frac{4}{3}-\frac{m}{m+M}{\cos }^2\theta \right)l\frac{\sin \theta }{\cos \theta }{\left(\frac{d\theta }{dt}\right)}^2+\frac{m}{m+M}l\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2-g\sin \theta =0\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{3g\cos \theta }{4l}\end{array}}$

Sustituyendo en la expresión de la energía, obtendremos el ángulo límite θ_l que forma la escalera con la vertical en el instante t_l

${\displaystyle \begin{array}{l}E=\frac{P^2}{2(m+M)}+\left(\frac{2}{3}-\frac{m{\cos }^2\theta }{2(m+M)}\right)m{l}^2\frac{3g\cos \theta }{4l}+mgl\cos \theta \\ E=\frac{P^2}{2(m+M)}+\frac{3}{2}mgl\cos \theta -\frac{3}{8}\frac{m^{2}gl}{m+M}{\cos }^3\theta \end{array}}$

Las condiciones iniciales especificadas hacen que la constante P=0 y la energía inicial E=mglcosθ₀. Igualamos la energía inicial y la energía en el instante límite t_l

${\displaystyle \cos {\theta }_0=\frac{3}{2}\cos \theta -\frac{3}{8}\frac{m}{m+M}{\cos }^3\theta }$

Obtenemos una ecuación cúbica en cosθ. La raíz real buscada cosθ_l estará comprendida entre 0 y 1

En el instante límite t_l, la posición x_l y velocidad v_l de la pared móvil serán

${\displaystyle \begin{array}{l}{x}_l=\frac{P}{m+M}{t}_l-\frac{ml}{m+M}\left(\sin {\theta }_l-\sin {\theta }_0\right)\\ {\frac{dx}{dt}|}_l=\frac{P}{m+M}-\frac{ml}{m+M}\cos {\theta }_l{\left(\frac{d\theta }{dt}\right)}_l=\frac{P}{m+M}-\frac{ml}{m+M}\cos {\theta }_l\sqrt{\frac{3g\cos {\theta }_l}{4l}}\end{array}}$

Las condiciones iniciales especificadas hacen que la constante P=0

${\displaystyle \begin{array}{l}{x}_l=-\frac{ml}{m+M}\left(\sin {\theta }_l-\sin {\theta }_0\right)\\ v_l=-\frac{ml}{m+M}\cos {\theta }_l\sqrt{\frac{3g\cos {\theta }_l}{4l}}\end{array}}$

En la situación incial, la pared móvil de masa M se encuentra en la posición x=0 y el centro de masas de la escalera de masa m en lsinθ₀. En el instante t_l, la pared móvil se encuentra en x_l y el centro de masa de la escalera en lsinθ_l+x_l. En un sistema aislado, si el centro de masas del conjunto de los dos cuerpos estaba inicialmente en resposo, sigue en reposo en la misma posición

${\displaystyle \begin{array}{l}\frac{M·0+ml\sin {\theta }_0}{m+M}=\frac{M{x}_l+m\left(ml\sin {\theta }_l+x_l\right)}{m+M}\\ x_l=-\frac{ml}{m+M}\left(\sin {\theta }_l-\sin {\theta }_0\right)\end{array}}$

Como el centro de masas del conjunto de los dos cuerpos está en reposo, se cumple que M·v_l+m·v_cm=0

Siendo v_cm la velocidad horizontal del centro de masas de la escalera

Primera etapa del movimiento

• Masa de la escalera, m=1
• Longitud de la escalera, 2l=1
• Masa de la pared móvil, M=2
• Posición inicial de la pared móvil, x=0
• Velocidad inicial de la pared móvil, dx/dt=0
• Angulo inicial de la escalera con la vertical, θ₀=π/6. La escalera se suelta en esta posición, (dθ/dt)₀=0

Con estas condiciones iniciales la constante P=0

Calculamos el ángulo límite θ_l, cuando la escalera deja de estar en contacto con la pared móvil. Calculamos las raíces de la ecuación cúbica y elegimos la raíz real entre 0 y 1. Utilizamos la función raices_3 o alternativamente, el comando roots

Resolvemos la ecuación diferencial en θ, mediante ode45 e interrumpimos el proceso de integración cuando θ=θ_l definiendo la función stop_escalera

function escalera_bloque
    L=0.5; %longitud de la escalera, 2L
    M=2; %masa de la pared móvil
    m=1; %masa de la escalera
    th_0=pi/6; %ángulo inicial

%ángulo límite final
    raiz=raices_3([3*m/(8*(m+M)),0,-3/2,cos(th_0)]);
    for i=1:length(raiz)
        if raiz(i)>0 && raiz(i)<1
            th_L=acos(raiz(i));
            break;
        end
    end
    f=@(t,x) [x(2); (9.8/L-m*cos(x(1))*x(2)^2/(m+M))*sin(x(1))/
(4/3-m*cos(x(1))^2/(m+M))]; 
    opts=odeset('events',@(t,x) stop_escalera(t,x, th_L));
    [t,x]=ode45(f,[0,10],[th_0,0],opts);
    plot(t,x(:,1));
    
    %posición final e instante
    disp([th_L*180/pi,t(end)])
    %velocidad y posición final de la pared móvil
    vPared=-m*cos(th_L)*sqrt(3*9.8*L*cos(th_L))/(2*(m+M)); 
    xPared=-m*L*(sin(th_L)-sin(th_0))/(m*M);
    disp([xPared,vPared])

    set(gca,'YTick',0:pi/12:pi/2)
    set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
    grid on
    xlabel('t')
    ylabel('\theta')
    title('Escalera, pared móvil')

%conservación de la energía
    E0=m*9.8*L*cos(th_0); %energía inicial
    %energía final
    E=m*L^2*(2/3-m*cos(x(end,1)).^2/(2*(m+M))).*x(end,2).^2+m*9.8*L*cos(x(end,1));
    disp([E0,E])

%detiene el proceso de integración ode45 cuando se alcanza el ángulo límite
    function [value,isterminal,direction]=stop_escalera(~,x, th_L)
        value=x(1)-th_L;  
        isterminal=1;
        direction=1; 
    end

%raíces de una ecuación cúbica
    function x = raices_3(p)
        for i=4:-1:1
            p(i)=p(i)/p(1);
        end
        Q=(p(2)*p(2)-3*p(3))/9;
        R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
        x=zeros(3,1); %reserva memoria para un vector de tres elementos
        if (R*R)<(Q^3)
            tetha=acos(R/sqrt(Q^3));
            x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
            x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
            x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
        else
            A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
            if A==0
                B=0;
            else
                B=Q/A;
            end
            x(1)=(A+B)-p(2)/3;
            x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*1i; 
            x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*1i;
        end
    end
end

53.4949    0.2917
-0.0760   -0.2932
4.2435    4.2438

Los resultados son:

• Angulo límite, θ_l=53.5°
• Instante en el que se alcanza esta posición, t_l=0.29
• Posición de la pared móvil en este instante, x_l=-0.076
• Velocidad de la pared móvil en este instante, v_l=-0.29
• Energía inicial, E=4.2435, parecida a la energía final E=4.2438

Representamos la posición angular θ de la escalera en función del tiempo t hasta el instante t_l

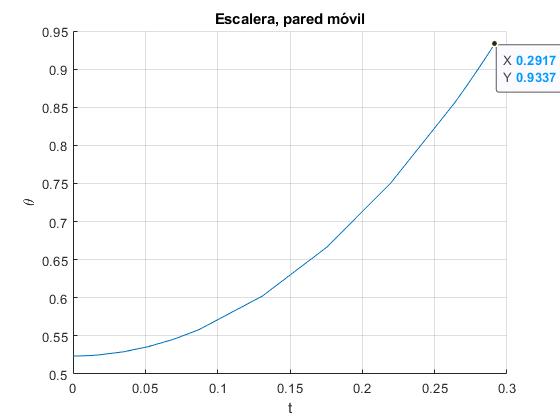
Sea θ₀=π/6, la posición angular inicial de la escalera. Si hacemos que la masa de la pared móvil sea grande, por ejemplo M=20, obtenemos un ángulo θ_l=54.6°, muy próximo al que se obtiene considerando una pared fija (véase la fórmula al principio de esta página)

>> acos(2*cos(pi/6)/3)*180/pi
ans =   54.7356

Segunda etapa del movimiento

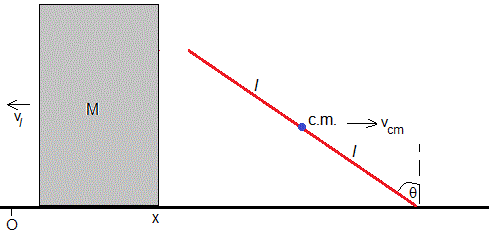
La pared móvil de masa M se mueve hacia la izquierda con velocidad constante v_l

La constancia del momento lineal en un sistema aislado, implica que el centro de masa de la escalera se mueve con velocidad constante v_cm hacia la derecha, tal que, m·v_cm+Mv_l=0

En el sistema de referencia que se mueve con el centro de masa de la escalera, su posición y velocidad es

${\displaystyle \begin{array}{l}{y}_c=l\cos \theta \\ \frac{d{y}_c}{dt}=-l\sin \theta \frac{d\theta }{dt}\end{array}}$

La energía cinética de la escalera es la suma de la energía cinética de traslación del c.m. y de la energía cinética de rotación alrededor de un eje perpendicular que pasa por el c.m.

${\displaystyle E_k=\frac{1}{2}m{\left(\frac{dy}{dt}\right)}^2+\frac{1}{2}\left(\frac{1}{3}m{l}^2\right){\left(\frac{d\theta }{dt}\right)}^2=\frac{1}{2}m{l}^2\left(\frac{1}{3}+{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial del c.m. de la escalera es E_p=mglcosθ. La lagrangiana es

${\displaystyle L=\frac{1}{2}m{l}^2\left(\frac{1}{3}+{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2-mgl\cos \theta }$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \left(\frac{1}{3}+{\sin }^2\theta \right)\frac{d^2\theta }{d{t}^2}+\sin \theta \cos \theta {\left(\frac{d\theta }{dt}\right)}^2-\frac{g}{l}\sin \theta =0\end{array}}$

La misma que hemos obtenido en la página titulada Escalera apoyada en dos paredes perpendiculares, en la sección, 'El extremo B de la escalera deja de estar en contacto con la pared vertical'

Resolvemos esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t_l, el ángulo que forma la escalera con la vertical es θ_l y su velocidad angular de rotación es

${\displaystyle {\left(\frac{d\theta }{dt}\right)}_l=\frac{1}{2}\sqrt{\frac{3g\cos {\theta }_l}{l}}}$

Cuando la escalera impacta con el suelo, θ=π/2, emplea un tiempo t_f en alcanzarlo. La posición de la pared móvil y del c.m. de la escalera serán

${\displaystyle \begin{array}{l}{x}_f=x_l+v_l(t_f-t_l)\\ x_{cm}=l\sin {\theta }_l+v_{cm}(t_f-t_l)=l\sin {\theta }_l-\frac{M}{m}{v}_l(t_f-t_l)\end{array}}$

ya que durante este intervalo de tiempo se mueven con velocidad constante v_l y v_cm, respectivamente

Movimiento completo

Resolvemos la ecuación diferencial en θ, mediante ode45 e interrumpimos el proceso de integración cuando θ=π/2 definiendo la función stop_escalera_1

function escalera_bloque
L=0.5; %longitud de la escalera 2L
M=2; %masa de la pared móvil
m=1; %masa de la escalera
th_0=pi/6; %ángulo inicial

%ángulo límite
raiz=raices_3([3*m/(8*(m+M)),0,-3/2,cos(th_0)]);
for i=1:length(raiz)
    if raiz(i)>0 && raiz(i)<1
        th_L=acos(raiz(i));
        break;
    end
end

%primera etapa
f=@(t,x) [x(2); (9.8/L-m*cos(x(1))/(m+M))*sin(x(1))/(4/3-m*cos(x(1))^2/(m+M))]; 
opts=odeset('events',@(t,x) stop_escalera(t,x, th_L));
[t,x]=ode45(f,[0,10],[th_0,0],opts);
hold on
plot(t,x(:,1));
tL=t(end); %final de la primera etapa
%velocidad final de la pared móvil
vPared=-m*cos(th_L)*sqrt(3*9.8*L*cos(th_L))/(2*(m+M)); 
line([tL,tL],[0,th_L],'color','k','lineStyle','--')
line([0,tL],[th_L,th_L],'color','k','lineStyle','--')

%segunda etapa
opts=odeset('events',@stop_escalera_1);
f=@(t,x) [x(2);(9.8/L-cos(x(1))*x(2)^2)*sin(x(1))/(1/3+sin(x(1))^2)]; 
[t,x]=ode45(f,[0,10],[th_L,sqrt(3*9.8*cos(th_L)/L)/2],opts);
plot(t+tL,x(:,1))
disp(t(end)+tL) %tiempo total
hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('t')
ylabel('\theta')
title('Escalera, pared móvil')

%conservación de la energía
E0=m*9.8*L*cos(th_0);
E=M*(m+M)*vPared^2/(2*m)+m*L^2*(1/3+sin(x(end,1))^2)*x(end,2).^2
/2+m*9.8*L*cos(x(end,1));
disp([E0,E])
%velocidad angular final
wf=3*9.8*(cos(th_0)-3*M*cos(th_L)^3/(8*(m+M)))/(2*L);
disp([sqrt(wf),x(end,2)])

%detiene el proceso de integración ode45 cuando se alcanza el ángulo límite
function [value,isterminal,direction]=stop_escalera(~,x, th_L)
    value=x(1)-th_L;  
    isterminal=1;
    direction=1; 
end

%detiene el proceso de integración ode45 cuando se alcanza el ángulo pi/2
function [value,isterminal,direction]=stop_escalera_1(~,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

%raíces de una ecuación cúbica
function x = raices_3(p)
    for i=4:-1:2
        p(i)=p(i)/p(1);
    end
    %p(4)=p(4)/p(1);
    %p(2)=p(2)/p(1);
    %p(3)=p(3)/p(1);
    p(1)=1;
    Q=(p(2)*p(2)-3*p(3))/9;
    R=(2*p(2)^3-9*p(2)*p(3)+27*p(4))/54;
    x=zeros(3,1); %reserva memoria para un vector de tres elementos
    if (R*R)<(Q^3)
        tetha=acos(R/sqrt(Q^3));
        x(1)=-2*sqrt(Q)*cos(tetha/3)-p(2)/3;
        x(2)=-2*sqrt(Q)*cos((tetha+2*pi)/3)-p(2)/3;
        x(3)=-2*sqrt(Q)*cos((tetha-2*pi)/3)-p(2)/3;
    else
        A=-sign(R)*nthroot(abs(R)+sqrt(R*R-Q^3),3);
        if A==0
            B=0;
        else
            B=Q/A;
        end
        x(1)=(A+B)-p(2)/3;
        x(2)=-(A+B)/2-p(2)/3+(sqrt(3)*(A-B)/2)*1i; 
        x(3)=-(A+B)/2-p(2)/3-(sqrt(3)*(A-B)/2)*1i;
    end
end
end

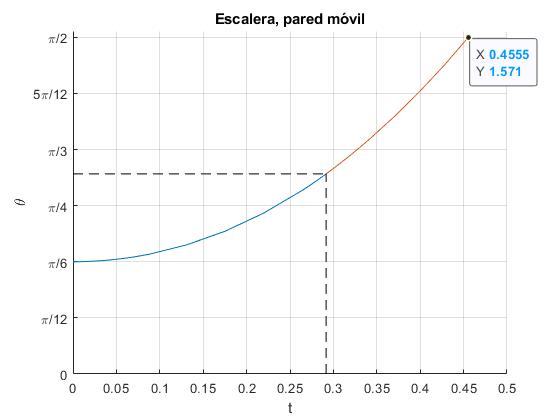
Representamos la posición angular θ de la escalera en función del tiempo t desde el instante t=0, hasta el instante t_l y desde el instante t_l hasta el instante t_f cuando la escalera ha impactado en el suelo θ=π/2

La energía en la segunda etapa del movimiento es

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}_{cm}^2+\frac{1}{2}M{v}_l^2+\frac{1}{2}m{l}^2\left(\frac{1}{3}+{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta =\\ \frac{1}{2}M\left(1+\frac{M}{m}\right)v_l^2+\frac{1}{2}m{l}^2\left(\frac{1}{3}+{\sin }^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta \end{array}}$

Igualamos la energía inicial mglcosθ₀ a la final, cuando θ=π/2, despejamos la velocidad angular dθ/dt en la posición final

${\displaystyle \begin{array}{l}mgl\cos {\theta }_0=\frac{1}{2}M\left(1+\frac{M}{m}\right)v_l^2+\frac{2}{3}m{l}^2{\left(\frac{d\theta }{dt}\right)}^2\\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{3g}{2l}\left(\cos {\theta }_0-\frac{3}{8}\frac{M}{\left(M+m\right)}{\cos }^3{\theta }_l\right)\end{array}}$

Comprobamos que la energía incial es similar a la final y que la velocidad angular dθ/dt final es similar a la que nos proporciona el procedimiento numérico x(end,2)

    4.2435    4.2417 %energía
    4.8902    4.8890 %velocidad angular final

Actividades

Se introduce

• El ángulo inicial θ₀ que forma la escalera con la vertical, en el control titulado Angulo
• La masa M de la pared móvil, en el control titulado Masa pared

El programa interactivo ha fijado los parámetros

• La longitud de la escalera, 2l=1
• La masa de la escalera, m=1
• La pared móvil parte del origen en reposo, x=0, dx/dt=0
• La escalera se deja caer desde su posición inicial θ₀, por lo que dθ/dt=0

Se pulsa el botón titulado Nuevo

Observamos que la escalera empieza a caer, a la vez que la pared se mueve hacia la izquierda del origen

Una flecha de color azul muestra la fuerza F_x que ejerce la escalera sobre la pared móvil, mientras la escalera está en contacto con dicha pared. Medimos el ángulo critico θ_l cuando dicha fuerza se hace cero, el mensaje 'En contacto' desaparece

En la parte derecha, se proporcionan los datos de

• El tiempo, t
• El ángulo θ que hace la escalera con la vertical en grados
• La posición de la pared móvil x
• La posición horizontal x_cm del centro de masa de la escalera

Después de que la escalera impacte con el suelo, la pared móvil y la escalera siguen moviéndose con velocidad constante, aunque en la simulación parece que se detengan

Referencias

Daniel Arovas. Lecture Notes on Classical Mechanics (A Work in Progress). University of California, San Diego. May 8, 2013, pp. 393-396. https://courses.physics.ucsd.edu/2010/Fall/physics200a/LECTURES/200_COURSE.pdf