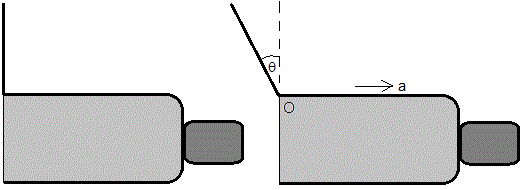
Las fuerzas de inercia son fuerzas ficticias, que surgen cuando se describe el movimiento de un cuerpo en un sistema de referencia acelerado. La fuerza centrífuga es la que experimenta un cuerpo cuando describimos su movimiento en un sistema de referencia en rotación. Cuando viajamos en un autobús que acelera o frena, experimentamos una fuerza, de sentido contrario a la aceleración.

Si la furgoneta acelera con aceleración constante a, en el centro de masa de la puerta de masa m actúa una fuerza ma, tal como se muestra en la figura.

Aplicando el teorema de Steiner calculamos el momento de inercia de una placa rectangular de masa m y achura L respecto del eje que pasa por O.

${\displaystyle I_O=\frac{1}{12}m{L}^2+m{\left(\frac{L}{2}\right)}^2=\frac{1}{3}m{L}^2}$

La ecuación de la dinámica de rotación de la puerta que gira alrededor de un eje que pasa por O

${\displaystyle \begin{array}{l}\left(\frac{1}{3}m{L}^2\right)\frac{d^2\theta }{d{t}^2}=ma\frac{L}{2}\cos \theta \\ \frac{d^2\theta }{d{t}^2}=\frac{3a\cos \theta }{2L}\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, θ=0, dθ/dt=0

L=1; %anchura de la puerta
a=2; %aceleración

f=@(t,x)[x(2); 3*a*cos(x(1))/(2*L)];
opts=odeset('events',@puerta_ode45);
[t,x,te]=ode45(f,[0,10],[0,0], opts);
plot(t,x(:,1))
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
text(0.1,pi-0.2,num2str(te)) %tiempo que tarda en cerrarse la puerta
grid on
xlabel('t')
ylabel('\theta');
title('Posición angular en función del tiempo')

Definimos una función para que el proceso de integración se detenga cuando la posición de la puerta sea muy próxima a π

function [detect,stopin,direction]=puerta_ode45(t,x)
    detect=x(1)-pi+0.002; 
    stopin=1;
    direction=1; 
end

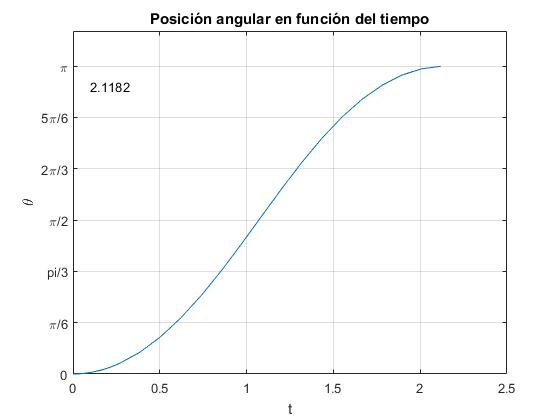
La puerta tarda 2.12 s en cerrarse

Integramos esta ecuación diferencial con las condiciones iniciales t=0, θ=0, dθ/dt=0

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=\frac{3a}{2L}\cos \theta \hfill \\ \frac{d\omega }{d\theta }\frac{d\theta }{dt}=\frac{3a}{2L}\cos \theta \omega \frac{d\omega }{d\theta }=\frac{3a}{2L}\cos \theta \hfill \\ \underset{0}{\overset{\omega }{{\displaystyle \int }}}\omega ·d\omega =\frac{3a}{2L}\underset{0}{\overset{\theta }{{\displaystyle \int }}}\cos \theta ·d\theta \hfill \\ \frac{1}{2}{\omega }^2=\frac{3a}{2L}\sin \theta \hfill \\ {\left(\frac{d\theta }{dt}\right)}^2=\frac{3a}{L}\sin \theta \hfill \end{array}}$

El tiempo t que tarda en cerrarse la puerta es

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\sqrt{\frac{3a}{L}\sin \theta }\\ t=\sqrt{\frac{L}{3a}}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{\sin \theta }}}\end{array}}$

Calculamos la integral definida utilizando procedimientos numéricos. El integrando tiende a infinito en los dos límites de integración, sin embargo, la función integral de MATLAB no produce error

>> f=@(x) 1./sqrt(sin(x)); 
>> tFin=integral(f,0,pi)*sqrt(L/(3*a))
tFin =    2.1409

La furgoneta se habrá desplazado en este tiempo

${\displaystyle x=\frac{1}{2}a{t}^2=\frac{L}{6}{\left({\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{\sin \theta }}}\right)}^2}$

La distancia que recorre la furgoneta hasta que se cierra el portón trasero es independiente de la aceleración a

Actividades

Se introduce

• La aceleración a en el control titulado Aceleración
• La anchura L=1 m se ha fijado en el programa interactivo

Se pulsa el botón titulado Nuevo

Fuerzas sobre la puerta

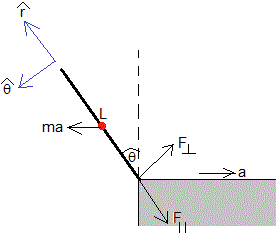
Además de la fuerza de inercia ma, que actúa en el centro de masa, el eje ejerce una fuerza F formando un ángulo desconocido sobre la puerta o bien, dos fuerzas mutuamente perpendiculares:

• Una fuerza paralela a la puerta, F_||
• Una fuerza perpendicular a la puerta, F_⊥

Para calcular estas dos fuerzas, adoptamos coordenadas polares. En otras páginas de este capítulo, hemos deducido la expresión el vector velocidad y el vector aceleración en coordenadas polares.

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\hfill \\ \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$

En esta caso r=L/2 es constante

Las ecuaciones del movimiento del c.m. en la dirección radial $\widehat{r}$

${\displaystyle -m\frac{L}{2}{\left(\frac{d\theta }{dt}\right)}^2=ma\sin \theta -F_{\parallel }}$

Esta es la ecuación de la dinámica del movimiento circular del centro de masa de la puerta que describe un arco de circunferencia de radio L/2

Conocida la velocidad angular de rotación, despejamos F_||

${\displaystyle F_{\parallel }=\frac{5}{2}ma\sin \theta }$

La ecuación del movimiento en la dirección $\widehat{\theta }$

${\displaystyle m\frac{L}{2}\frac{d^2\theta }{d{t}^2}=ma\cos \theta -F_{\perp }}$

Conocida la aceleración angular, despejamos la fuerza F_⊥

${\displaystyle F_{\perp }=\frac{1}{4}ma\cos \theta }$

en el sentido indicado en la figura

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1203, pp. 328-330