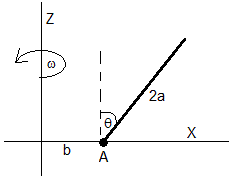
Una varilla de masa m y longitud 2a gira alrededor del eje Z con velocidad angular constante ω, tal como se muestra en la figura. La varilla puede girar libremente en el plano XZ alrededor del punto A de sujeción.

Estudiamos el equilibrio de la varilla en el Sistema en Referencia en Rotación, (no inercial) X', Z', que se mueve con velocidad angular constante.

La energía cinética de la varilla, que gira alrededor de un eje perpendicular y que pasa por su extremo A es

${\displaystyle E_k=\frac{1}{2}\left(\frac{1}{12}m{\left(2a\right)}^2+m{a}^2\right){\left(\frac{d\theta }{dt}\right)}^2=\frac{1}{2}\left(\frac{4}{3}m{a}^2\right){\left(\frac{d\theta }{dt}\right)}^2}$

Para determinar las posiciones de equilibrio solamente precisamos de la energía potencial, que se compone de dos términos: la energía potencial gravitatoria y la centrífuga

Energía potencial

La energía potencial gravitatoria, E_g=mgacosθ

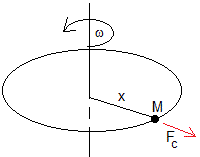
La fuerza centrífuga depende solamente de la distancia x al eje de rotación, es una fuerza conservativa similar a la que ejerce de un muelle elástico.

La fuerza que ejerce un muelle elástico es de sentido contrario al desplazamiento F=-kx, su energía potencial es positiva E_p=kx²/2

La fuerza centrífuga tiene el mismo sentido que el desplazamiento F_c=mω ²·x

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}m{\omega }^{2}x·dx}=0-E_p}$

y su energía potencial será por tanto negativa $E_c=-\frac{1}{2}m{\omega }^2{x}^2$ . La energía potencial inicial para x=0, se toma como E_c=0.

Para una distribución de masa como la representada por la varilla de masa m, longitud 2a, inclinada un ángulo θ, la energía potencial centrífuga es

${\displaystyle \begin{array}{l}{E}_c=-{\displaystyle \underset{0}{\overset{2a}{\int }}\frac{1}{2}{\omega }^2{\left(b+x\sin \theta \right)}^2}dm=-\frac{1}{2}{\omega }^2\frac{m}{2a}{\displaystyle \underset{0}{\overset{2a}{\int }}{\left(b+x\sin \theta \right)}^2}dx=\\ -\frac{m}{2}{\omega }^2\left(b^2+2ab\sin \theta +\frac{4}{3}{a}^3{\sin }^2\theta \right)=-\frac{m}{2}{\omega }^2\left\{{\left(b+a\sin \theta \right)}^2+\frac{1}{3}{a}^2{\sin }^2\theta \right\}\end{array}}$

La energía potencial total es la suma E_p=E_c+E_g

${\displaystyle E_p=mga\cos \theta -\frac{1}{2}m{\omega }^2\left\{{\left(b+a\sin \theta \right)}^2+\frac{1}{3}{a}^2{\sin }^2\theta \right\}}$

Representamos la energía E_p en función del ángulo θ en el intervalo [0,2π]

a=1; %longitud de la varilla 2a
b=0.5; %distancia al extremo A
w=3; %velocidad angular de rotación
%energía potencial
eP=@(x) 9.8*a*cos(x)-w^2*((b+a*sin(x)).^2+a^2*sin(x).^2/3)/2;
fplot(eP,[0,2*pi])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
grid on
xlabel('\theta')
ylabel('E_p(\theta)')
title('Energía potencial')

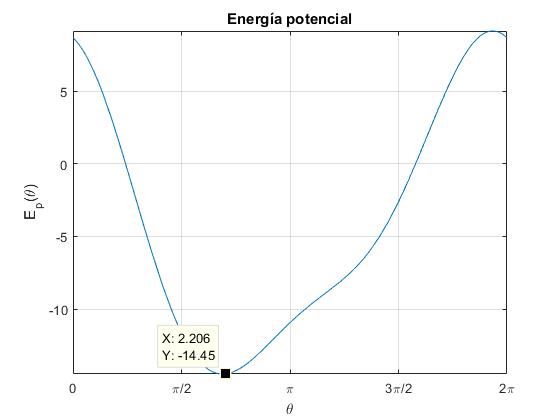
Para a=1 (longitud de la varilla 2a=2), distancia del eje de giro al extremo A, b=0.5, cuando gira con velocidad angular ω=3 rad/s, observamos una mínimo en el segundo cuadrante [π/2, π] y un máximo en el cuarto [3π/2,2π]

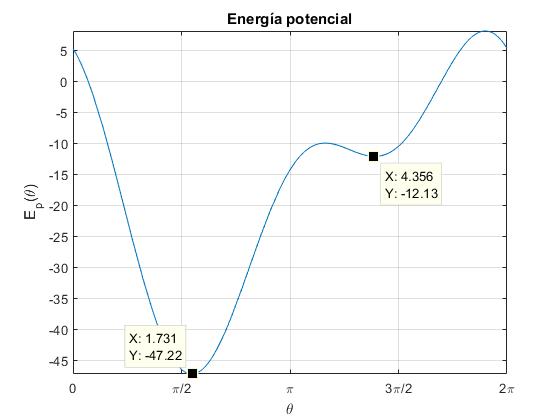
Incrementamos la velocidad angular a ω=6 rad/s, observando un mínimo y un máximo en el tercer cuadrante [π, 3π/2]

Para una velocidad angular muy grande, los mínimos se acercan a π/2 y a 3π/2. El segundo mínimo desaparece a medida que se incrementa b, quedando una sola posición de equilibrio estable a grandes velocidades angulares

Equilibrio

Las posiciones de equilibrio de la varilla son los extremos de la función energía potencial E_p(θ)

${\displaystyle \begin{array}{l}\frac{d{E}_p}{d\theta }=-mga\sin \theta -m{\omega }^{2}a\left\{b+\frac{4}{3}a\sin \theta \right\}\cos \theta \\ -g\sin \theta -{\omega }^2\left\{b+\frac{4}{3}a\sin \theta \right\}\cos \theta =0\\ \tan \theta =-\frac{{\omega }^{2}a}{g}\left(\frac{b}{a}+\frac{4}{3}\sin \theta \right)\end{array}}$

Las posiciones θ de equilibrio son los puntos de intersección de las funciones tanθ y f(θ)

${\displaystyle f(\theta )=-\frac{{\omega }^{2}a}{g}\left(\frac{b}{a}+\frac{4}{3}\sin \theta \right)}$

a=1; %longitud de la varilla 2a
b=0.5; %posición del extremo A
w=6; %velocidad angular de rotación
hold on
fplot(@(x) tan(x),[0,2*pi])
f=@(x) -a*w^2*(b/a+4*sin(x)/3)/9.8;
fplot(f,[0,2*pi])
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
ylim([-10,10])
hold off
grid on
xlabel('\theta')
ylabel('f(\theta)')
title('Angulos de equilibrio')

Para a=1 (longitud de la varilla 2a=2), distancia del eje de giro al extremo A, b=0.5, cuando gira con velocidad angular ω=3 rad/s, observamos una intersección en el segundo cuadrante [π/2, π] y otra en el cuarto [3π/2,2π], que corresponden al mínimo y al máximo de la energía potencial representada en la primera figura

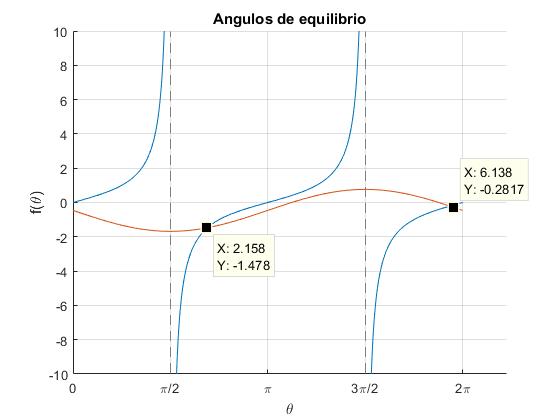
Incrementamos la velocidad angular a ω=6 rad/s, observando varias intersecciones en el segundo, tercer y cuarto cuadrante que se corresponden con los máximos y mínimos de la energía potencial

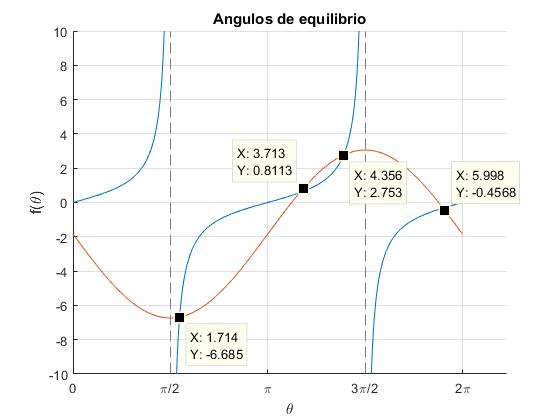
Estabilidad

para determinar si el equilibrio es estable o inestable, comprobamos el signo d ela derivada segunda de la energía potencial E_p(θ)

${\displaystyle \begin{array}{l}\frac{d^2{E}_p}{d{\theta }^2}=-mga\cos \theta -\frac{4}{3}m{\omega }^2{a}^2{\cos }^2\theta +m{\omega }^{2}a\left\{b+\frac{4}{3}a\sin \theta \right\}\sin \theta =\\ -\frac{4}{3}m{\omega }^2{a}^2\left({\cos }^2\theta -{\sin }^2\theta \right)+m{\omega }^{2}ab\sin \theta -mga\cos \theta \end{array}}$

Introduciendo la condición de equilibrio

${\displaystyle \begin{array}{l}g\sin \theta =-{\omega }^2\left\{b+\frac{4}{3}a\sin \theta \right\}\cos \theta \\ \frac{d^2{E}_p}{d{\theta }^2}=\frac{m{\omega }^{2}a{\cos }^2\theta }{\sin \theta }\left(\frac{4}{3}a{\tan }^2\sin \theta +b{\tan }^2\theta +b\right)=\\ \frac{m{\omega }^{2}a{\cos }^2\theta }{\sin \theta }\left(\left\{\frac{4}{3}a\sin \theta +b\right\}{\tan }^2\theta +b\right)\end{array}}$

Volviendo a introducir la condición de equilibrio, llegamos a la expresión más simplificada de la derivada segunda de la energía potencial

${\displaystyle \begin{array}{l}\tan \theta =-\frac{{\omega }^2}{g}\left(b+\frac{4}{3}a\sin \theta \right)\\ \frac{d^2{E}_p}{d{\theta }^2}=\frac{ma{\cos }^2\theta }{\sin \theta }\left(-g{\tan }^3\theta +b{\omega }^2\right)\end{array}}$

• En el segundo cuadrante [π/2,π], sinθ>0 y tanθ<0

${\displaystyle \frac{d^2{E}_p}{d{\theta }^2}>0}$

el equilibrio es estable, tal como hemos visto en representación de E_p(θ)

• En el cuarto cuadrante, [3π/2,2π] sinθ<0 y tanθ<0

${\displaystyle \frac{d^2{E}_p}{d{\theta }^2}<0}$

El equilibrio es inestable, tal como hemos visto en representación de E_p(θ)

• En el tercer cuadrante, [π,3π/2], escribimos la derivada segunda de la forma

${\displaystyle \begin{array}{l}\frac{d^2{E}_p}{d{\theta }^2}=\frac{m{\omega }^{2}a{\cos }^2\theta }{\sin \theta }\left(\frac{4}{3}a{\tan }^2\theta \sin \theta +b{\tan }^2\theta +b\right)=\frac{m{\omega }^{2}a{\cos }^2\theta }{\sin \theta }\left(\frac{4}{3}a{\tan }^2\theta \sin \theta +\frac{b}{{\cos }^2\theta }\right)\\ =\frac{m{\omega }^{2}a}{\sin \theta }\left(\frac{4}{3}a{\sin }^3\theta +b\right)\end{array}}$

Como sinθ<0, se pueden producir dos casos:

${\displaystyle b>\frac{4}{3}a\left|{\sin }^3\theta \right|}$

La derivada segunda es negativa, el equilibrio es inestable, en caso contrario, la derivada segunda es positiva y el equilibrio es estable

Cálculo de las posiciones de equilibrio estable

Calculamos las raíces de la ecuación trascendente

${\displaystyle \tan \theta +\frac{{\omega }^{2}a}{g}\left(\frac{b}{a}+\frac{4}{3}\sin \theta \right)=0}$

Partiendo de las posiciones de equilibrio aproximadas que nos da la representación gráfica. Calculamos las posiciones de equilibrio utilizando la función fzero de MATLAB. Evaluamos para cada raíz la derivada segunda,

Una vez calculadas las posiciones de equilibrio, evaluamos para cada raíz la derivada segunda, para determinar si es una posición de equlibrio estable o inestable

${\displaystyle \frac{d^2{E}_p}{d{\theta }^2}=-\frac{4}{3}m{\omega }^2{a}^2\left({\cos }^2\theta -{\sin }^2\theta \right)+m{\omega }^{2}ab\sin \theta -mga\cos \theta }$

Finalmente, representamos la varilla en las posiciones de equilibrio estable (en azul), o inestable (en rojo). Las líneas vertical y horizontal a trazos son el eje X' y el eje Z', en el Sistema de Referencia que gira con velocidad angular constante ω

a=1; %longitud de la varilla 2a
b=0.5; %posición del extremo A
w=6; %velocidad angular de rotación

raiz=[1.714,3.713,4.356,5.998]; %posiciones aproximadas
%derivada primera
g=@(x) tan(x)+a*w^2*(b/a+4*sin(x)/3)/9.8;
%derivada segunda
ff=@(x) -4*w^2*a*(cos(x)^2-sin(x)^2)/3+w^2*b*sin(x)-9.8*cos(x);

for i=1:length(raiz)
    raiz(i)=fzero(g,raiz(i)); %posiciones de equilibrio
    fprintf('ángulo %1.3f, derivada segunda, %1.3f\n',raiz(i),ff(raiz(i)));
end

line([0,0],[0,2*a],'lineStyle','--')
line([-a,a],[0,0],'lineStyle','--')
for i=1:length(raiz)
    if ff(raiz(i))>0 
        line([b,b+2*a*cos(raiz(i))],[0,2*a*sin(raiz(i))],'lineWidth',2,'color','b')
    else
        line([b,b+2*a*cos(raiz(i))],[0,2*a*sin(raiz(i))],'lineWidth',2,'color','r')
    end
end

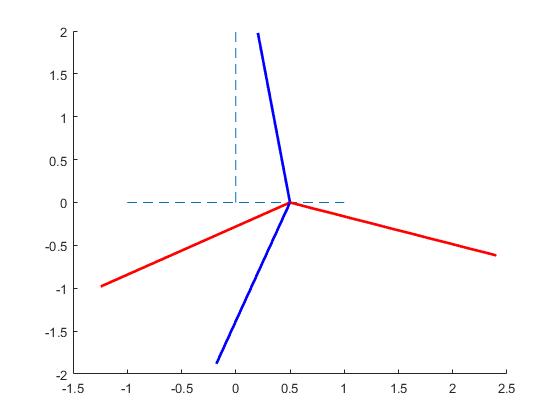
ángulo 1.719, derivada segunda, 65.149
ángulo 3.653, derivada segunda, -25.252
ángulo 4.366, derivada segunda, 23.330
ángulo 5.969, derivada segunda, -53.728

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1223, pp. 364-367