Momento de inercia

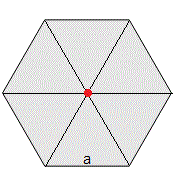
Calculamos el momento de inercia de un lápiz de sección hexagonal, de masa m y lado a, respecto del eje paralelo al lápiz y que pasa por el centro (punto de color rojo)

El momento de inercia de un hexágono es seis veces el momento de inercia de un triángulo equilátero de lado a respecto de uno de los vértices.

Calculamos la altura h y el área del triángulo equilátero de lado a

${\displaystyle \begin{array}{l}h=a\frac{\sqrt{3}}{2}\\ \frac{a·h}{2}=a^2\frac{\sqrt{3}}{4}\end{array}}$

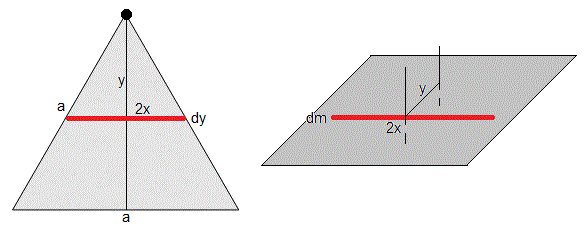
Para calcular el momento de inercia del triángulo respecto de un eje perpendicular al plano que lo contiene y que pasa por su vértice, dividimos el triángulo en franjas de longitud 2x y anchura dy, tal como se muestra en la figura.

Sabiendo que el momento de inercia de una varilla de longitud L respecto de un eje perpendicular a la varilla y que pasa por su punto medio es mL²/12. Aplicando el teorema de Steiner calculamos el momento de inercia de la franja de masa dm, longitud 2x respecto al eje paralelo que pasa por el vértice distante y.

${\displaystyle \frac{1}{12}dm{\left(2x\right)}^2+y^{2}dm=\left(\frac{x^2}{3}+y^2\right)dm}$

Relacionamos las variables x e y, tan30=x/y.

${\displaystyle x=\frac{y}{\sqrt{3}}}$

Sabiendo que la masa del hexágono es m y que la masa de un triángulo equilátero es m/6. La masa dm de la franja de longitud 2x y anchura dy es

${\displaystyle dm=\frac{m/6}{\sqrt{3}{a}^2/4}2x·dy=\frac{4m}{9a^2}y·dy}$

El momento de inercia del triángulo es la suma de los momentos de inercia de las franjas comprendidas entre y=0 e y=h

${\displaystyle I_3={\displaystyle \underset{0}{\overset{a\sqrt{3}/2}{\int }}\left(\frac{y^2}{9}+y^2\right)}\frac{4m}{9a^2}y·dy=\frac{40}{81}\frac{m}{a^2}{\displaystyle \underset{0}{\overset{a\sqrt{3}/2}{\int }}{y}^3}·dy=\frac{5}{72}m{a}^2}$

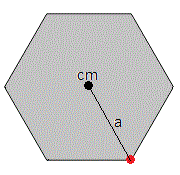
El momento de inercia del hexágono, es 6 veces este valor

${\displaystyle I_{cm}=\frac{5}{12}m{a}^2}$

Aplicamos el teorema de Steiner para calcular el momento de inercia del hexágono respecto de un eje paralelo que pasa por un vértice, distante a (en color rojo).

${\displaystyle I=\frac{5}{12}m{a}^2+m{a}^2=\frac{17}{12}m{a}^2}$

Conservación de la energía

Vamos a estudiar el movimiento de un lápiz de sección hexagonal de masa m, lado a, situado sobre un plano inclinado α

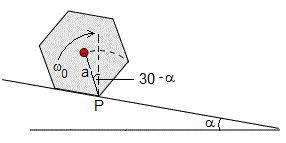
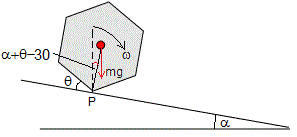
El lápiz gira alrededor de un eje fijo que pasa por su vértice P. El c.m. del lápiz (punto de color rojo) describe un arco de circunferencia de radio a y ángulo π/3. En la figura, se muestra la situación inicial, el ángulo de giro θ=0 y la velocidad angular inicial es ω₀

La energía del lápiz en la posición inicial es la suma de la energía cinética de rotación alrededor del eje que pasa por el vértice P y la energía potencial del centro de masa del lápiz, que está a una altura acos(α-π/6) sobre P, tal como vemos en la figura

${\displaystyle E=\frac{1}{2}I{\omega }_0^2+mga\cos \left(\frac{\pi }{6}-\alpha \right)}$

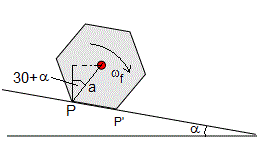
En la figura se muestra el lápiz en la situación final, cuando ha completado un giro de 60° alrededor del eje que pasa por el vértice P. La velocidad angular de rotación es ω_f y el centro del lápiz está a una altura acos(π/6+α) sobre P. El nuevo eje de rotación pasa por el vértice P' distante a de P

${\displaystyle E=\frac{1}{2}I{\omega }_f^2+mga\cos \left(\frac{\pi }{6}+\alpha \right)}$

Conocida la velocidad angular inicial ω₀, calculamos la velocidad angular final ω_f, aplicando el principio de conservación de la energía

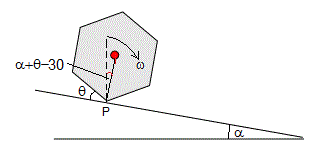
En general, cuando el lápiz ha girado un ángulo θ alrededor del eje que pasa por el vértice P, su velocidad angular de rotación será ω

${\displaystyle E=\frac{1}{2}I{\omega }^2+mga\cos \left(\alpha +\theta -\frac{\pi }{6}\right)}$

Choque de una cara del lápiz con el plano inclinado

Supondremos que una pequeña proporción (1-ε) de la energía cinética final se pierde en el choque de una de las caras del lápiz con el plano inclinado. La nueva energía cinética inicial, cuando el lápiz empieza a girar alrededor del eje que pasa por el vértice P', es

${\displaystyle \begin{array}{l}\frac{1}{2}I{\omega }_0^2=\epsilon \frac{1}{2}I{\omega }_f^2\\ {\omega }_0=\sqrt{\epsilon }{\omega }_f\end{array}}$

Este es el mecanismo de disipación de la energía que hace que el lápiz adquiera una velocidad constante después de cierto tiempo. El parámetro ε, no tiene que coincidir con el coeficiente de restitución, ya que la distribución de fuerzas cuando entran en contacto una cara del lápiz y el plano inclinado no es homogénea

Situación inicial

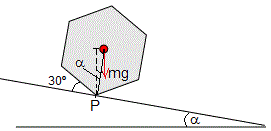
En la situación inicial el lápiz se ha girado θ=π/6, tal como se muestra en la figura, la velocidad angular inicial es cero. El lápiz se suelta empezando su movimiento a lo largo del plano inclinado.

La velocidad angular final del lápiz antes de experimentar el primer choque con el plano inclinado es

${\displaystyle mga\cos \left(\alpha \right)=\frac{1}{2}I{\omega }_f^2+mga\cos \left(\frac{\pi }{6}+\alpha \right)}$

Relación de recurrencia

El movimiento del lápiz consta de dos etapas:

• Movimiento de rotación de 60° alrededor de un eje fijo que pasa por el vértice situado en P

Conocida la velocidad angular inicial ω₀, calculamos la velocidad angular final ω_f, aplicando el principio de conservación de la energía

${\displaystyle $ \begin{array}{l}\frac{1}{2}I{\omega }_0^2+mga\cos \left(\frac{\pi }{6}-\alpha \right)=\frac{1}{2}I{\omega }_f^2+mga\cos \left(\frac{\pi }{6}+\alpha \right)\\ \frac{1}{2}I{\omega }_0^2+mga\sin \left(\alpha \right)=\frac{1}{2}I{\omega }_f^2\end{array}$}$

Para obtener este resultado utilizamos la relación trigonométrica, cos(A-B)-cos(A+B)=2sinA·sinB. Con A=π/6 y B=α.

ω₀ es la velocidad angular al comienzo θ=0 de la rotación alrededor del eje que pasa por el vértice situado en P y ω_f es la velocidad angular al final cuando θ=π/3 .

• Choque de una cara del lápiz con el plano inclinado

La velocidad inicial ω₀ para la siguiente rotación alrededor de un eje que pasa por P' distante a, se calcula mediante la relación

${\displaystyle \frac{1}{2}I{\omega }_0^2=\epsilon \frac{1}{2}I{\omega }_f^2}$

Buscamos una expresión para la velocidad angular de rotación justamente antes del n choque de una cara del lápiz con el plano inclinado, cuando el eje de rotación que pasa por un vértice se encuentra en la posición x=(n-1)a.

1. Sea E_k0 la energía cinética de rotación del lápiz justo antes del primer choque, cuando el eje de rotación pasa por el vértice situado en x=0,

${\displaystyle E_{k0}=mga\left(\cos \alpha -\cos \left(\frac{\pi }{6}+\alpha \right)\right)}$

2. Justo antes del segundo choque, cuando el eje de rotación pasa por el vértice situado en x=a, la energía cinética es E_k1.

${\displaystyle E_{k1}=\epsilon E_{k0}+mga\sin \alpha }$

3. Justo antes del tercer choque, cuando el eje de rotación pasa por el vértice situado en xx=2a, la energía cinética es E_k2.

${\displaystyle \begin{array}{l}{E}_{k2}=\epsilon E_{k1}+mga\sin \alpha \\ E_{k2}=\epsilon \left(\epsilon E_{k0}+mga\sin \alpha \right)+mga\sin \alpha ={\epsilon }^2{E}_{k0}+\left(1+\epsilon \right)mga\sin \alpha \end{array}}$

4. Justo antes del cuarto choque, cuando el eje de rotación pasa por el vértice situado en x=3a, la energía cinética es E_k3.

${\displaystyle \begin{array}{l}{E}_{k3}=\epsilon E_{k2}+mga\sin \alpha \\ E_{k3}=\epsilon \left({\epsilon }^2{E}_{k0}+\left(1+\epsilon \right)mga\sin \alpha \right)+mga\sin \alpha ={\epsilon }^3{E}_{k0}+\left(1+\epsilon +{\epsilon }^2\right)mga\sin \alpha \end{array}}$

5. Justo antes del choque n, cuando el eje de rotación pasa por el vértice situado en x=(n-1)a, la energía cinética es E_kn-1.

${\displaystyle \begin{array}{l}{E}_{kn-1}=\epsilon E_{kn-2}+mga\sin \alpha \\ E_{kn-1}={\epsilon }^{n-1}{E}_{k0}+\left(1+\epsilon +\mathrm{...}+{\epsilon }^{n-2}\right)mga\sin \alpha \\ E_{kn-1}={\epsilon }^{n-1}{E}_{k0}+\frac{1-{\epsilon }^{n-1}}{1-\epsilon }mga\sin \alpha \end{array}}$

Para que el lápiz continúe su movimiento, la energía después del choque de una de las caras con el plano inclinado, tiene que ser mayor que la energía potencial máxima mga, que se produce cuando θ=π/6-α.

${\displaystyle \begin{array}{l}\epsilon E_{kn-1}+mga\cos \left(\frac{\pi }{6}-\alpha \right)>mga\\ E_{kn-1}>\frac{mga}{\epsilon }\left(1-\cos \left(\frac{\pi }{6}-\alpha \right)\right)\end{array}}$

El estado estacionario

Cuando n es grande

${\displaystyle \begin{array}{l}{E}_{k\infty }=\frac{1}{1-\epsilon }mga\sin \alpha \\ {\omega }_{\infty }=\sqrt{\frac{24g\sin \alpha }{17(1-\epsilon )a}}\end{array}}$

La velocidad angular final de rotación ω_∞, no depende de la situación inicial de partida. Otra forma de deducirla es

En el estado estacionario la velocidad final ω_f=ω_∞, y la velocidad inicial ω₀ para la siguiente rotación es

${\displaystyle \frac{1}{2}I{\omega }_0^2=\epsilon \frac{1}{2}I{\omega }_{\infty }^2}$

La conservación de la energía se expresa

${\displaystyle \epsilon \frac{1}{2}I{\omega }_{\infty }^2+mga\sin \alpha =\frac{1}{2}I{\omega }_{\infty }^2}$

En otras palabras, la energía cinética que se gana en la rotación de π/3 se pierde en el choque de una de las caras del lápiz contra el plano inclinado. Despejamos la velocidad angular final

${\displaystyle {\omega }_{\infty }=\sqrt{\frac{24g}{17(1-\epsilon )a}\sin \alpha }}$

El estado transitorio y su evolución hacia el estado estacionario

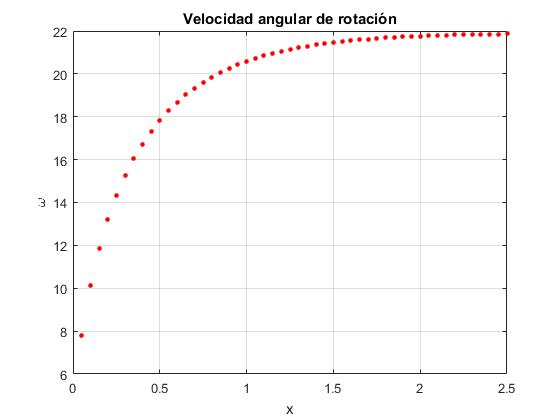
Mediante el código MATLAB, calculamos la velocidad final ω_f, justamente antes del choque de una cara del lápiz con el plano inclinado. Representamos esta velocidad en función de la posición del eje que pasa por el vértice del lápiz

a=0.05; %radio
I0=17*a*a/12; %momento de inercia
alfa=10*pi/180; %inclinación
epsilon=0.9; %proporción
v=zeros(1,50);
E=9.8*a*cos(alfa); %energía inicial
for i=1:50
    Ek=E-9.8*a*cos(pi/6+alfa);
    v(i)=sqrt(2*Ek/I0); %al finalizar la rotación
    E=epsilon*Ek+a*9.8*cos(pi/6-alfa); %al comienzo de la siguiente rotación
end
plot((1:50)*a,v, 'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
grid on
xlabel('x')
ylabel('\omega')
title('Velocidad angular de rotación')

Ecuación del movimiento

Escribimos la ecuación de la dinámica de rotación alrededor de un eje fijo que pasa por P.

Cuando la cara que estaba en contacto con el plano inclinado ha girado un ángulo θ, el momento del peso mg respecto del eje que pasa por P es mga·sin(α+θ-π/6)

${\displaystyle I\frac{d^2\theta }{d{t}^2}=mga\sin \left(\theta +\alpha -\frac{\pi }{6}\right)}$

Se resuelve la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=0, (dθ/dt)₀=ω₀

Se interrumpe la ejecución del procedimiento numérico cuando θ=π/3. La velocidad angular final ω_f=(dθ/dt)_π/3.

El eje que pasa por el vértice P' distante a de P es el nuevo eje fijo de rotación, se pone el contador del tiempo parcial a cero, se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=0, (dθ/dt)₀=ω₀ con

${\displaystyle {\omega }_0=\sqrt{\epsilon }{\omega }_f}$

y así, sucesivamente

Las condiciones iniciales en el momento que se pone el lápiz sobre el plano inclinado y se suelta (véase el apartado titulado 'Situación inicial'), son: t=0, θ=π/6, (dθ/dt)₀=0

a=0.05; %radio
I0=17*a^2/12;
alfa=10*pi/180; %inclinación
epsilon=0.9; %proporción
v=zeros(1,20);
tf=zeros(1,20);
f=@(t,x) [x(2);9.8*a*sin(x(1)+alfa-pi/6)/I0]; 
opts=odeset('events',@hexagono_ode45);
tt=0;
hold on
x0=[pi/6,0];
for i=1:20
    [t,x,te,xe,ie]=ode45(f,[0,10],x0, opts);
    plot(tt+t,x(:,2),'b') %velocidad angular
    tf(i)=t(end)+tt;
    tt=tt+te;
    v(i)=xe(2);  %al finalizar la rotación
    x0=[0, sqrt(epsilon)*xe(2)];
end
plot(tf,v, 'ro','markersize',3,'markeredgecolor','r','markerfacecolor','r')
grid on
xlabel('t')
ylabel('\omega_f')
title('Velocidad angular de rotación')

Se define una función que detiene el proceso de integración cuando θ=π/3

function [detect,stopin,direction]=hexagono_ode45(t,x)
    detect=x(1)-pi/3; 
    stopin=1;
    direction=1; 
end

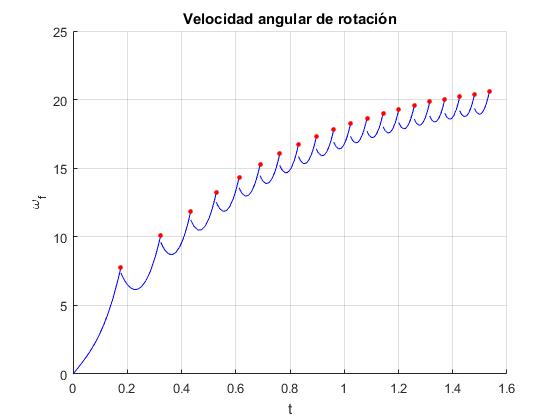
Hemos representado la velocidad angular de rotación en función del tiempo t. Observamos que cuando se alcanza el estado estacionario, el tiempo P entre dos choques consecutivos se mantiene aproximadamente constante. La velocidad del c.m. del lápiz será el cociente a/P

El lápiz deja de estar en contacto con el plano inclinado

El c.m. del lápiz describe un arco de circunferencia de radio a. La ecuación de la dinámica del movimiento circular se escribe

${\displaystyle mg\cos \left(\alpha +\theta -\frac{\pi }{6}\right)-N=m{\omega }^{2}a}$

El primer término es la componente del peso en la dirección radial, el segundo, N es la reacción del plano inclinado sobre el vértice P y ω²a es la aceleración normal

N tiene que ser positivo para cualquier valor de 0<θ<π/6

${\displaystyle g\cos \left(\alpha +\theta -\frac{\pi }{6}\right)\ge {\omega }^{2}a}$

El valor mínimo de la componente del peso, corresponde a θ=π/6 y la velocidad angular mayor posible es ω_∞

${\displaystyle \begin{array}{l}g\cos \left(\alpha +\frac{\pi }{6}\right)\ge {\omega }_{\infty }^{2}a\\ \tan \alpha \le \frac{6\sqrt{3}\left(1-\epsilon \right)}{\left(17+6\left(1-\epsilon \right)\right)}\end{array}}$

Para ε=0.9, obtenenos tanα≤0.06 (3.4°)

Actividades

Se introduce

• El valor de ε, en el control titulado Parámetro ε
• El ángulo α del plano inclinado, en el control titulado Angulo α
• El lado de la sección hexagonal se ha fijado en a=5 cm
• La masa del lápiz se ha fijado en m=1

Se pulsa el botón titulado Nuevo

Se observa el movimiento del lápiz y la representación de la velocidad final de rotación ω_f, justamente antes del choque de una cara del lápiz con el plano inclinado. En el eje horizontal tenemos la posición del eje de rotación P.

Referencias

Amin Rezaeezadeh. Motion of a hexagonal pencil on a inclined plane. Am. J. Phys. 77 (5) May 2009, pp 401-406