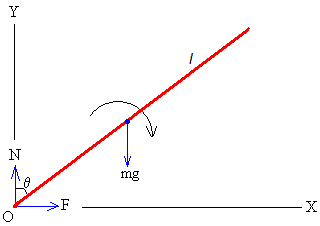
Consideraremos el lápiz como una varilla delgada homogénea de masa m y longitud l. Las fuerzas sobre el lápiz son

• El peso mg que actúa en el centro de masas

• La reacción del suelo N que actúa en el punto de contacto P

• La fuerza de rozamiento F que actúa en el mismo punto.

Las ecuaciones del movimiento son la composición de:

1. Movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=F\\ m\frac{d^{2}y}{d{t}^2}=N-mg\end{array}}$

2. Movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{l}{2}\text{sin}\theta -F\frac{l}{2}\cos \theta }$

θ es el ángulo que forma el lápiz con el eje vertical Y en el instante t.

I_c es el momento de inercia de una varilla de masa m y longitud l respecto de un eje perpendicular a la varilla que pasa por el c.m.

${\displaystyle I_c=\frac{1}{12}m{l}^2}$

El movimiento del lápiz consta de dos etapas

• La punta del lápiz está en reposo en contacto con el suelo mientras la fuerza |F|<μN

• La punta del lápiz desliza sobre el suelo cuando la fuerza |F|≥μN

La punta del lápiz está en reposo en contacto con el suelo

Se trata del mismo problema que la caída de una varilla inclinada sujeta por uno de sus extremos, con un planteamiento distinto.

Si la punta del lápiz está en contacto con el suelo, la posición del centro de masas es (véase la figura más arriba)

x=(l/2) sinθ, 
 y=(l/2) cosθ

Las componentes rectangulares de la velocidad y aceleración del centro de masas son, respectivamente

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{l}{2}\cos \theta \frac{d\theta }{dt}\\ \frac{d^{2}x}{d{t}^2}=\frac{l}{2}\left\{-\text{sin}\theta {\left(\frac{d\theta }{dt}\right)}^2+\cos \theta \frac{d^2\theta }{d{t}^2}\right\}\\ \frac{dy}{dt}=-\frac{l}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{l}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Las fuerzas horizontal y vertical en el punto de apoyo P valen

${\displaystyle \begin{array}{l}F=m\frac{l}{2}\left\{-\text{sin}\theta {\left(\frac{d\theta }{dt}\right)}^2+\cos \theta \frac{d^2\theta }{d{t}^2}\right\}\\ N=mg-m\frac{l}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

La ecuación del movimiento de rotación alrededor de un eje que pasa por el c.m.

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{3g}{2l}\text{sin}\theta }$     (1)

Esta es la ecuación diferencial que obtuvimos para el movimiento de caída de la varilla con su extremo O fijo.

Para obtener el ángulo θ que hace la varilla con el suelo en función del tiempo, se integra la ecuación diferencial mediante procedimientos numéricos con las condiciones iniciales siguientes: en el instante t=0, la varilla está inclinada un ángulo θ=θ₀ y parte del reposo, ω=dθ/dt=0

Aproximación

Cuando el ángulo θ es pequeño podemos hacer la aproximación sinθ≈θ. La ecuación diferencial se escribe

${\displaystyle \frac{d^2\theta }{d{t}^2}-\frac{3g}{2l}\theta =0}$

Cuya solución es

${\displaystyle \theta =A\exp \left(\sqrt{\frac{3g}{2l}}t\right)+B\exp \left(-\sqrt{\frac{3g}{2l}}t\right)}$

Los coeficientes A y B se determinan  a partir de las condiciones iniciales: en el instante t=0, la varilla está inclinada un ángulo θ=θ₀ y parte del reposo, ω=dθ/dt=0

${\displaystyle \theta =\frac{{\theta }_0}{2}\left\{\exp \left(\sqrt{\frac{3g}{2l}}t\right)+\exp \left(-\sqrt{\frac{3g}{2l}}t\right)\right\}}$

El desplazamiento angular θ crece exponencialmente con el tiempo.

Estudio energético

La energía potencial del c.m. de la varilla E=mg(l/2)·cosθ₀ se convierte en energía cinética de rotación. El principio de conservación de la energía se escribe.

${\displaystyle mg\frac{l}{2}\text{cos}{\theta }_0=\frac{1}{2}{I}_0{\omega }^2+mg\frac{l}{2}\text{cos}\theta }$       

Donde I_o es el momento de inercia de una varilla de masa m y longitud l respecto de un eje perpendicular a la varilla que pasa por el punto de contacto O con el suelo. Aplicando teorema de Steiner

${\displaystyle I_0=\frac{1}{12}m{l}^2+m{\left(\frac{l}{2}\right)}^2=\frac{1}{3}m{l}^2}$

Despejamos la velocidad angular de rotación alrededor del punto fijo O

${\displaystyle \omega =\frac{d\theta }{dt}=\sqrt{\frac{3g}{l}(\cos {\theta }_0-\cos \theta )}}$       (2)

Introducimos dθ/dt y d²θ/dt², ecuaciones (1) y (2), en las expresiones de la fuerza horizontal y vertical en el punto de apoyo, F y N

${\displaystyle \begin{array}{l}F=\frac{3mg}{4}\text{sin}\theta (3\cos \theta -2\cos {\theta }_0)\\ N=mg-\frac{3mg}{4}(1+2\cos \theta \cos {\theta }_0-3{\cos }^2\theta )\end{array}}$

Que son las mismas expresiones que obtuvimos al estudiar la caída de una varilla inclinada sujeta por uno de sus extremos. Hemos llegado a la misma solución pero con un planteamiento distinto.

En la figura, se muestra el valor del cociente F/N en función del ángulo θ, cuando el lápiz se inclina ligeramente θ₀=1º respecto de la posición vertical y se suelta.

${\displaystyle \frac{F}{N}=\frac{3(3\cos \theta -2\cos {\theta }_0)\text{sin}\theta }{1+9{\cos }^2\theta -6\cos \theta \cos {\theta }_0}}$

th_0=1*pi/180; %ángulo inicial
f=@(x) 3*(3*cos(x)-2*cos(th_0)).*sin(x)./(1+9*cos(x).^2-6*cos(x)*cos(th_0));
fplot(f,[0,pi/3])
grid on
ylim([-0.4,0.4])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta')
ylabel('F/N')
title('Cociente F/N')

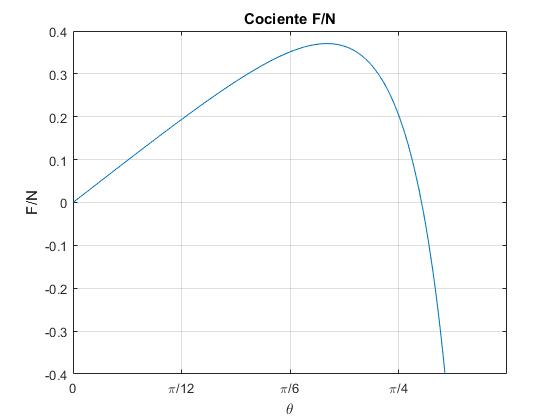
Cuando θ₀≈0, cosθ₀≈1, el denominador proporcional a N es el cuadrado (1-3cosθ)² que es positivo.

Fuerza nula

El cociente F/N alcanza un valor máximo para un ángulo próximo a 35º, y F se hace cero para un ángulo próximo a 48º. Finalmente, F cambia de signo.

F y por tanto, el cociente F/N se hace cero cuando

3cosθ=2cosθ₀,

Si el lápiz se libera cuando hace un ángulo θ₀ próximo a cero, cosθ₀≈1

cosθ=2/3, θ=48.2º

Máximo y mínimo

Algo más laborioso resulta calcular el ángulo θ para el cual F/N presenta un máximo. Derivamos el cociente F/N respecto del ángulo θ e igualamos a cero

(-3sin²θ+3cos²θ-2cosθ·cosθ₀)(1+9cos²θ-6cosθ·cosθ₀)-(3cosθ-2·cosθ₀)·sinθ (-18cosθ +6cosθ₀)·sinθ =0

Realizando algunas operaciones y empleando la relación trigonométrica sin²θ=1-cos²θ llegamos a la ecuación de segundo grado

33cos²θ-38cosθ·cosθ₀-3+12·cos²θ₀=0

Una de las raíces corresponde a un máximo y la otra a un mínimo

${\displaystyle \cos \theta =\frac{38\cos {\theta }_0\pm \sqrt{396-140{\cos }^2{\theta }_0}}{66}}$

Si el lápiz se suelta cuando hace un ángulo θ₀ próximo a cero, cosθ₀≈1

Las raíces son cosθ₁=1/3 y cosθ₂=9/11

Los correspondientes ángulos son θ₁=70.5º y θ₂=35.1º. La primera N→0 y F/N→-∞ (es un mínimo), la segunda (F/N)_máx=0.371 es un máximo tal como se aprecia en la figura más arriba.

La punta del lápiz desliza

F y N no son independientes sino que F=±μN

• Las ecuaciones del movimiento de traslación del centro de masas son

${\displaystyle m\frac{d^{2}x}{d{t}^2}=F=\pm \mu N}$

Si la punta del lápiz está apoyada en el suelo N>0, la ordenada y del centro de masas y el ángulo de giro θ de la varilla alrededor de un eje que pasa por el c.m. están relacionados y=(l/2) cosθ

${\displaystyle \begin{array}{l}\frac{dy}{dt}=-\frac{l}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{l}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Aplicando la segunda ley de Newton al movimiento vertical del c.m.

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=N-mg\\ N=mg-m\frac{l}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Expresión obtenida en la sección anterior

• Movimiento de rotación alrededor de un eje perpendicular al lápiz que pasa por su centro de masas, (suponemos inicialmente que F>0)

${\displaystyle \begin{array}{l}\frac{1}{12}M{l}^2\frac{d^2\theta }{d{t}^2}=N\frac{l}{2}\text{sin}\theta -\mu N\frac{l}{2}\cos \theta \\ \frac{d^2\theta }{d{t}^2}=\frac{\left(6g-3l{\left(\frac{d\theta }{dt}\right)}^2\cos \theta \right)(\text{sin}\theta -\mu \cos \theta )}{l(1+3\text{sin}\theta (\text{sin}\theta -\mu \cos \theta ))}\end{array}}$

Posición y velocidad de la punta del lápiz

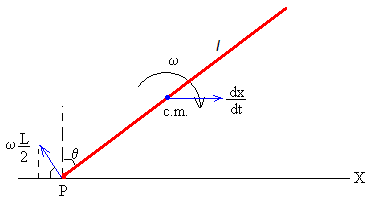
La velocidad de la punta del lápiz P, es la suma de la velocidad de traslación del c.m. dx/dt y la velocidad debida a la rotación alrededor de un eje perpendicular al lápiz y que pasa por el c.m. ωl/2

${\displaystyle v_P=\frac{dx}{dt}-\frac{l}{2}\frac{d\theta }{dt}\cos \theta }$

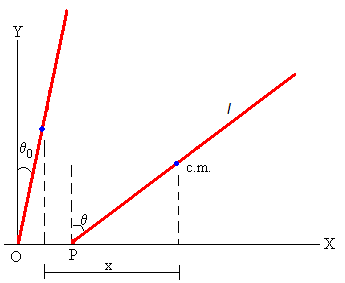
Si situamos el origen O en la punta del lápiz cuando se libera formando un ángulo θ₀, con la dirección vertical. El desplazamiento de la punta del lápiz es la distancia OP

OP=x+(l/2)sinθ₀-(l/2)sinθ

Donde x es el desplazamiento del centro de masas

Mientras la punta del lápiz P permanece en el origen en reposo, v_P=0, la velocidad del centro de masas dx/dt>0.

La punta del lápiz empieza a deslizar a partir del ángulo θ_d para el cual se cumple que |F|=μN.  Para calcular este ángulo, resolvemos la ecuación trascendente

${\displaystyle \mu =\left|\frac{3(3\cos \theta -2\cos {\theta }_0)\text{sin}\theta }{1+9{\cos }^2\theta -6\cos \theta \cos {\theta }_0}\right|}$           (3)

Casos particulares

Se consideran los casos

• El coeficiente de rozamiento μ>(F/N)_máx

La punta del lápiz empieza a deslizar cuando la fuerza horizontal F<0.

Ejemplo: sea μ=0.5>(F/N)_máx=0.371

mu=0.5; %coeficiente
th_0=1*pi/180; %ángulo inicial
fuerza=@(x) 3*sin(x).*(3*cos(x)-2*cos(th_0))/4; %fuerza de rozamiento
normal=@(x) 1-3*(1+2*cos(x)*cos(th_0)-3*cos(x).^2)/4; %reacción N
f=@(x) abs(fuerza(x)./normal(x))-mu;
th_d=fzero(f,[0,pi/2]); %ángulo empieza a deslizar
fuerza_d=@(x) -mu*normal(x);
hold on
fplot(fuerza,[0,th_d])
fplot(fuerza_d,[th_d,pi/2])
line([th_d,th_d],[0,fuerza(th_d)],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta')
ylabel('F/mg')
title('Fuerza de rozamiento')



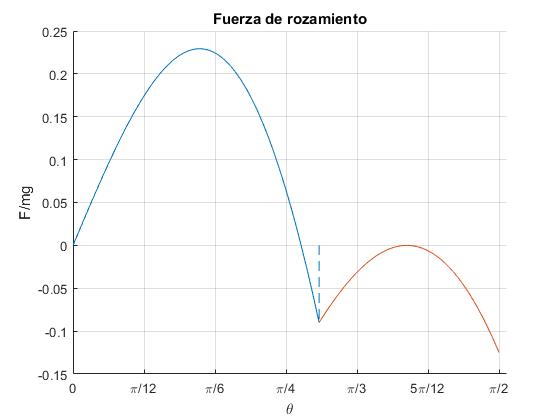
Una gráfica similar genera el programa interactivo al final de la página. Veremos que empieza a deslizar para el ángulo θ_d

>> th_d*180/pi
ans =   51.9851

Si el lápiz se libera cuando está inclinado un ángulo θ₀=1º respecto de la dirección vertical. Resolviendo la ecuación trascendente (3) obtenemos una raíz θ_d=52.0º

Para 0<θ<θ_d, la punta del lápiz permanece en reposo en el origen. La fuerza horizontal F en la punta del lápiz es primero positiva θ<48.2º y luego negativa.

Para θ_d≤θ<90º, la punta del lápiz desliza hacia la derecha. La fuerza horizontal en la punta del lápiz F=μN es negativa. El máximo desplazamiento de la punta del lápiz es x_P=9.2 mm

• El coeficiente de rozamiento μ<(F/N)_máx

La punta del lápiz empieza a deslizar cuando la fuerza horizontal F>0

F=μN>0 (ya que N es siempre positivo), la punta del lápiz se mueve hacia la izquierda v_P<0 y su velocidad va disminuyendo hasta que se detiene. La punta del lápiz permanecerá en reposo mientras la fuerza horizontal |F|< μN y deslizará en caso contrario.

Ejemplo: sea μ=0.15<(F/N)_máx=0.371



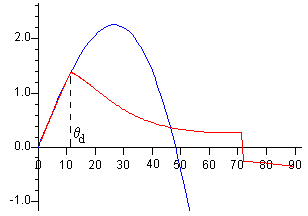
Si el lápiz se libera cuando está inclinado un ángulo θ₀=1º respecto de la dirección vertical. Resolviendo la ecuación trascendente (3) obtenemos una raíz θ_d=11.5º

Para 0<θ<11.5º, la punta del lápiz permanece en reposo en el origen. La fuerza horizontal F>0 en la punta del lápiz es positiva.

Para 11.5≤θ<71.5º, la punta del lápiz desliza hacia la izquierda v_P<0. La velocidad v_P primero aumenta (en valor absoluto) y luego, disminuye hasta que se hace cero en un ángulo próximo a θ=71.5º. La fuerza horizontal F es negativa para θ>48.2º y |F|> μN la velocidad de la punta del lápiz se hace positiva v_P>0, hasta el ángulo final θ=90º.

El comportamiento de la punta del lápiz es bastante complejo cuando μ≈(F/N)_máx=0.37. Se sugiere al lector probar con µ=0.35.

• El coeficiente de rozamiento μ=0

En este caso, no hay fuerza horizontal en la punta del lápiz F=0. El centro de masas no se mueve horizontalmente.

${\displaystyle m\frac{d^{2}x}{d{t}^2}=0}$

El ángulo que gira alrededor de un eje perpendicularmente al lápiz y que pasa por su c.m. es

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{\left(6g-3l{\left(\frac{d\theta }{dt}\right)}^2\cos \theta \right)\text{sin}\theta }{l(1+3{\text{sin}}^{\text{2}}\theta )}}$

Resultado que hemos obtenido en la página titulada “Lápiz que cae”

• El coeficiente de rozamiento μ es grande

El máximo ángulo θ_d=90º

${\displaystyle \mu =\left|\frac{3(3\cos 90-2\cos 1)\text{sin90}}{1+9{\cos }^{2}90-6\cos 90\cos 1}\right|=6·\cos 1=5.999}$

Cuando μ es mayor que este valor, el comportamiento del lápiz es similar al de una varilla que puede girar alrededor de su extremo fijo.

Actividades

Se introduce

• El coeficiente de rozamiento µ_s=µ_k=µ, entre la punta del lápiz y el suelo rugoso horizontal.

• La longitud del lápiz se ha fijado en l=0.2 m=20 cm

• El lápiz se libera cuando está inclinado un ángulo θ₀=1º respecto de la dirección vertical

Se pulsa el botón titulado Nuevo

Se observa la caída del lápiz hasta llegar al suelo θ=90º

En la parte izquierda se proporciona los datos de:

El tiempo t es segundos

• La posición x_P de la punta del lápiz en cm, situando el origen en la posición de la punta en el momento en que se libera θ₀=1º.

• La velocidad v_P de la punta del lápiz en cm/s

• La fuerza F_x horizontal F/m en N/kg

• La fuerza vertical F_y o reacción del plano horizontal N/m en N/kg

En la parte derecha se representa

• En color azul, la fuerza horizontal F/m, suponiendo que la punta del lápiz está fijada en el origen.

${\displaystyle F=\frac{3mg}{4}\text{sin}\theta (3\cos \theta -2\cos {\theta }_0)}$

La punta del lápiz empieza a deslizar a partir del ángulo θ_d para el cual se cumple que |F|=μN.

${\displaystyle N=mg-\frac{3mg}{4}(1+2\cos \theta \cos {\theta }_0-3{\cos }^2\theta )}$

• En color rojo, se representa la fuerza horizontal F/m cuando el lápiz está en reposo y cuando desliza.

Referencias

Cross R., The fall and bounce of pencils and other elongated objects. Am. J. Phys. 74 (1) January 2006, pp. 26-30