Escalera entre dos paredes con rozamiento

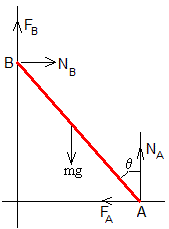
Supongamos una escalera homogénea de masa m y longitud l apoyada en dos paredes perpendiculares en los puntos A (lsinθ,0) y B (0, lcosθ,0), siendo θ el ángulo que forma la escalera con el eje vertical Y. Las fuerzas sobre la escalera son las que se ha dibujado en la figura.

• F_A y F_B son las fuerzas de rozamiento que ejercen las paredes vertical y horizontal en los respectivos apoyos.

• N_A y N_B son las reacciones de la pared en los puntos de apoyo

• mg es el peso que actúa en el centro de masas de la escalera a una distancia d de A. Si la escalera es homogénea d=l/2.

La situación de equilibrio solamente nos proporciona tres ecuaciones (dos para las fuerzas y una para los momentos), sin embargo, tenemos cuatro incógnitas, el problema es indeterminado.

${\displaystyle \begin{array}{l}\{\begin{array}{l}{F}_A=N_B\\ N_A+F_B=mg\end{array}\hfill \\ -F_{B}l\sin \theta -N_{B}l\cos \theta +mg\frac{l}{2}\sin \theta =0\hfill \end{array}}$

Seis troncos iguales apilados

En el problema 19 de Estática se describe el equilibrio de tres troncos apilados

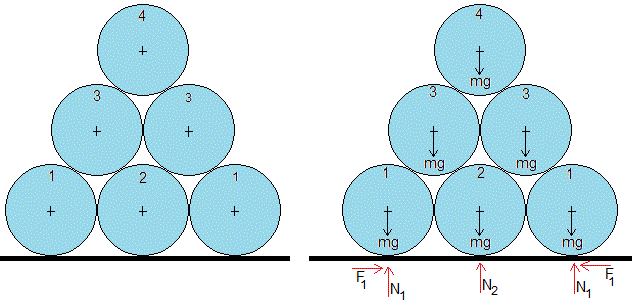
Se apilan seis troncos de madera de forma cilíndrica de la misma masa m y radio r. Aplicando la simetría y la tercera ley de Newton, las ecuaciones se simplifican notablemente.

Fuerzas exteriores

Fuerzas exteriores que actúan sobre el sistema de seis troncos apilados se muestran a la derecha en la figura. Se ha aplicado la condición de simetría a los troncos señalados por 1 y 1

• El peso, mg en el centro de cada tronco

• Las fuerzas N₁, N₂ y N₁, que ejercen el suelo sobre los troncos 1, 2 y 1 en el punto de contacto

• Las fuerzas de rozamiento, F₁ en los puntos de contacto de los troncos 1 y 1 con el suelo

En equilibrio

${\displaystyle 2N_1+N_2=6mg,(1)}$

Equilibrio del tronco 4

${\displaystyle \begin{array}{l}2N_{34}\cos 30=mg+2F_{34}\sin 30\\ \sqrt{3}{N}_{34}=mg+F_{34},(2)\end{array}}$

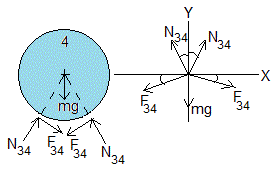
F₃₄ y N₃₄ son las fuerzas interiores que ejercen los troncos identificados con el número 3 sobre el tronco 4. DE nuevo, se ha utilizado la condición de simetría

Equilibrio del tronco 3

${\displaystyle \begin{array}{l}\{\begin{array}{l}{N}_{13}\cos 30+N_{23}\cos 30+F_{34}\sin 30=mg+F_{23}\sin 30+N_{34}\cos 30+F_{13}\sin 30\\ N_{13}\sin 30+F_{13}\cos 30=N_{23}\sin 30+F_{34}\cos 30+F_{23}\cos 30+N_{34}\sin 30\end{array}\\ \{\begin{array}{l}\sqrt{3}{N}_{13}+\sqrt{3}{N}_{23}+F_{34}=2mg+F_{23}+\sqrt{3}{N}_{34}+F_{13},(3)\\ N_{13}+\sqrt{3}{F}_{13}=N_{23}+\sqrt{3}{F}_{34}+\sqrt{3}{F}_{23}+N_{34},(4)\end{array}\end{array}}$

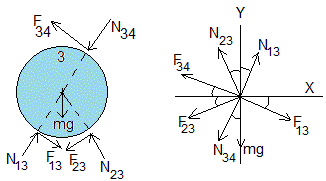
F₁₃ y N₁₃ son las fuerzas interiores que ejerce el tronco identificado con el número 1 sobre el tronco 3. F₂₃ y N₂₃ son las fuerzas interiores que ejerce el tronco identificado con el número 2 sobre el tronco 3

F₃₄ y N₃₄ son las fuerzas interiores que ejerce el tronco identificado con el número 4 sobre el tronco 3. Iguales y de sentido cotrario a los que ejerce el tronco 3 sobre el 4

Momentos respecto del centro del tronco

${\displaystyle \begin{array}{l}r{F}_{13}-r{F}_{23}+r{F}_{34}=0\\ F_{13}-F_{23}+F_{34}=\mathrm{0,}(5)\end{array}}$

Solución parcial

Resolvemos el sistema de cuatro ecuaciones (2), (3), (4) y (5) con seis incógnitas,

${\displaystyle \begin{array}{l}\{\begin{array}{l}\sqrt{3}{N}_{34}=mg+F_{34}\\ \sqrt{3}{N}_{13}+\sqrt{3}{N}_{23}+F_{34}=2mg+F_{23}+\sqrt{3}{N}_{34}+F_{13}\\ N_{13}+\sqrt{3}{F}_{13}=N_{23}+\sqrt{3}{F}_{34}+\sqrt{3}{F}_{23}+N_{34}\\ F_{13}-F_{23}+F_{34}=0\end{array}\\ N_{13}=N_{23}+7N_{34}-2\sqrt{3}mg\\ F_{23}=\sqrt{3}{N}_{23}+4\sqrt{3}{N}_{34}-5mg\\ F_{34}=\sqrt{3}{N}_{34}-mg\\ F_{13}=\sqrt{3}{N}_{23}+3\sqrt{3}{N}_{34}-4mg\end{array}}$

Equilibrio del tronco 1

F₁₃ y N₁₃ son las fuerzas interiores que ejerce el tronco identificado con el número 3 sobre el tronco 1. Iguales y de sentido cotrario a los que ejerce el tronco 1 sobre el 3

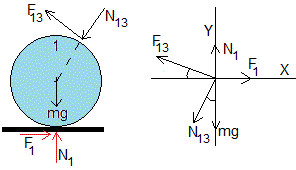
F₁ y N₁ son fuerzas exteriores al sistema

${\displaystyle \begin{array}{l}\{\begin{array}{l}{F}_1=F_{13}\cos 30+N_{31}\sin 30\\ N_1+F_{13}\sin 30=mg+N_{31}\cos 30\end{array}\\ \{\begin{array}{l}2F_1=\sqrt{3}{F}_{13}+N_{13},(6)\\ 2N_1+F_{13}=2mg+\sqrt{3}{N}_{13},(7)\end{array}\end{array}}$

Momentos respecto del centro del tronco

${\displaystyle \begin{array}{l}r{F}_1+r{F}_{13}=0\\ F_1+F_{13}=\mathrm{0,}(8)\end{array}}$

Equilibrio del tronco 2

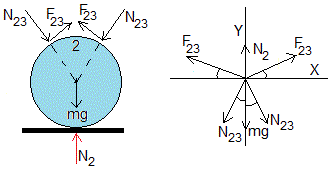
F₂₃ y N₂₃ son las fuerzas interiores que ejercen los troncos identificados con el número 3 sobre el tronco 2. Iguales y de sentido cotrario a los que ejerce el tronco 2 sobre el 3

N₂ es una fuerza exterior al sistema

${\displaystyle \begin{array}{l}{N}_2+2F_{23}\sin 30=mg+2N_{23}\cos 30\\ N_2+F_{23}=mg+\sqrt{3}{N}_{23},(9)\end{array}}$

Solución completa

Resolvemos el sistema de ecuaciones (1), (6), (7), (8) y (9)

${\displaystyle \{\begin{array}{l}2N_1+N_2=6mg\\ 2F_1=\sqrt{3}{F}_{13}+N_{13}\\ 2N_1+F_{13}=2mg+\sqrt{3}{N}_{13}\\ F_1+F_{13}=0\\ N_2+F_{23}=mg+\sqrt{3}{N}_{23}\end{array}}$

Eliminamos F₁ entre las ecuaciones segunda y cuarta

${\displaystyle N_{13}+\left(\sqrt{3}+2\right)F_{13}=0}$

Sustituimos F₁₃ y N₁₃ en la segunda y despejamos N₂₃

${\displaystyle \begin{array}{l}\left(N_{23}+7N_{34}-2\sqrt{3}mg\right)+\left(\sqrt{3}+2\right)\left(\sqrt{3}{N}_{23}+3\sqrt{3}{N}_{34}-4mg\right)=0\\ N_{23}=\frac{\left(4+3\sqrt{3}\right)mg-\left(8+3\sqrt{3}\right)N_{34}}{2+\sqrt{3}}=\left(2\sqrt{3}-1\right)mg-\left(7-2\sqrt{3}\right)N_{34}\end{array}}$

En la quinta ecuación, despejamos N₂

${\displaystyle \begin{array}{l}{N}_2+F_{23}=mg+\sqrt{3}{N}_{23}\\ N_2+\left(\sqrt{3}{N}_{23}+4\sqrt{3}{N}_{34}-5mg\right)=mg+\sqrt{3}{N}_{23}\\ N_2=6mg-4\sqrt{3}{N}_{34}\end{array}}$

En la primera ecuación, despejamos N₁

${\displaystyle \begin{array}{l}2N_1+N_2=6mg\\ 2N_1+\left(6mg-4\sqrt{3}{N}_{34}\right)=6mg\\ N_1=2\sqrt{3}{N}_{34}\end{array}}$

La última ecuación del sistema de cinco ecuaciones es la tercera

${\displaystyle \begin{array}{l}2N_1+F_{13}=2mg+\sqrt{3}{N}_{13}\\ 4\sqrt{3}{N}_{34}+\left(\sqrt{3}{N}_{23}+3\sqrt{3}{N}_{34}-4mg\right)=2mg+\sqrt{3}\left(N_{23}+7N_{34}-2\sqrt{3}mg\right)\\ 7\sqrt{3}{N}_{34}+\sqrt{3}{N}_{23}-4mg=2mg+\sqrt{3}{N}_{23}+7\sqrt{3}{N}_{34}-6mg\\ 7\sqrt{3}{N}_{34}+\sqrt{3}{N}_{23}-4mg=7\sqrt{3}{N}_{34}+\sqrt{3}{N}_{23}-4mg\end{array}}$

se reduce a una identidad, no nos permite despejar N₃₄

Con el dato de N₂₃ calculamos las incógnitas

${\displaystyle \begin{array}{l}{N}_{13}=N_{23}+7N_{34}-2\sqrt{3}mg=2\sqrt{3}{N}_{34}-mg\\ F_{23}=\sqrt{3}{N}_{23}+4\sqrt{3}{N}_{34}-5mg=3\left(2-\sqrt{3}\right)N_{34}-\left(\sqrt{3}-1\right)mg\\ F_{34}=\sqrt{3}{N}_{34}-mg\\ F_{13}=\sqrt{3}{N}_{23}+3\sqrt{3}{N}_{34}-4mg=\left(2-\sqrt{3}\right)mg+2\left(3-2\sqrt{3}\right)N_{34}\end{array}}$

El resultado final es el siguiente

${\displaystyle \begin{array}{l}{N}_2=6mg-4\sqrt{3}{N}_{34}\\ N_1=2\sqrt{3}{N}_{34},F_1=-F_{13}\\ N_{13}=2\sqrt{3}{N}_{34}-mg,F_{13}=\left(2-\sqrt{3}\right)mg+2\left(3-2\sqrt{3}\right)N_{34}\\ N_{23}=\left(2\sqrt{3}-1\right)mg-\left(7-2\sqrt{3}\right),F_{23}=3\left(2-\sqrt{3}\right)N_{34}-\left(\sqrt{3}-1\right)mg\\ F_{34}=\sqrt{3}{N}_{34}-mg\end{array}}$

Referencias

R. De Luca. Equilibrium of a wood stack formed by close-packed cylindrical logs. Revista Brasileira de Ensino de Física, vol. 46, e20240127 (2024)