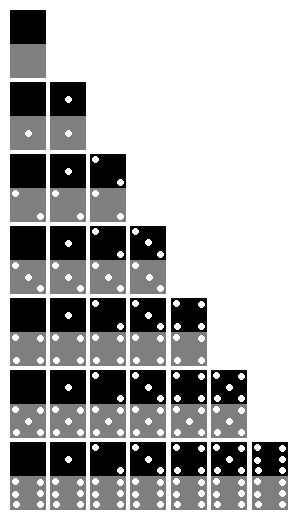
El dominó es un juego de mesa con 28 fichas rectangulares. La cara de la ficha está dividida en dos partes, numeradas mediante puntos de cero a seis, tal como se muestra en la figura. El número total de fichas es 28.

En cada turno, el jugador colocará una de sus fichas con la restricción de que dos fichas solamente pueden colocarse juntas cuando las mitades adyacentes sean del mismo valor.

El efecto dominó consiste en colocar las fichas (de altura l y anchura t) en posición vertical una al lado de la otra separadas una distancia d. Se empuja la primera ficha y se genera un tren de fichas que caen tal como se muestra en la figura.

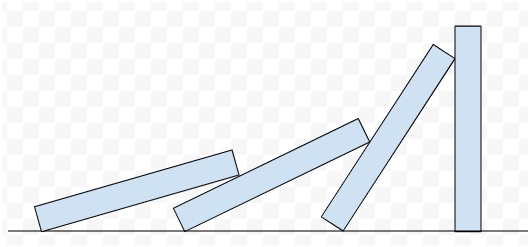
En esta página, calcularemos la velocidad de propagación v mediante un modelo simple que implica solamente a dos fichas.

Modelo simple

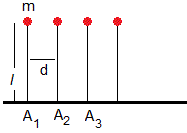
Representamos cada ficha por una varilla de longitud l de masa despreciable en cuyo extremo hay una partícula de masa m. La varilla puede girar alrededor de un eje perpendicular que pasa por el punto de contacto A_j. El coeficiente estático de rozamiento se supone suficientemente grande para que la varilla no deslice mientras cae. Las varillas están alineadas y separadas una distancia d

Choque elástico

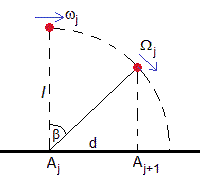
Describimos el choque de la ficha A_j con la ficha A_j+1. Cuando la ficha A_j gira un ángulo β tal que sinβ=d/l, la varilla A_j choca con la adyacente.

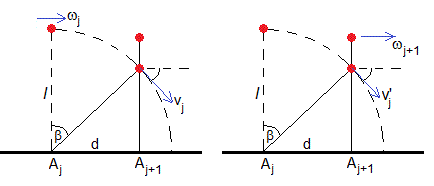
• Conservación del momento angular

Aplicamos la constancia del momento angular alrededor del eje perpendicular al plano de la figura que pasa por punto A_j+1

La velocidad de la partícula de masa m justamente antes del choque es v_j=Ω_jl. El momento angular inicial, respecto del punto A_j+1 es m·v_jcosβ(lcosβ)

${\displaystyle L_i=m{l}^2{\Omega }_j{\cos }^2\beta }$

Después del choque, la segunda varilla empieza a girar alrededor del A_j+1 con velocidad angular ω_j+1. La primera partícula después del choque se mueve tangencialmente con velocidad v'_j=Ω'_jl, su momento angular respecto del punto A_j+1 es m·v'_jcosβ(lcosβ). El momento angular final es

${\displaystyle L_f=\left(m{l}^2\right){\omega }_{j+1}+m{l}^2\Omega {\text{'}}_j{\cos }^2\beta }$

Siendo ml² el momento de inercia del sistema formado por la varilla de longitud l y masa despreciable y la partícula de masa m situada en su extremo

Igualando el momento angular inicial y final, obtenemos

${\displaystyle {\Omega }_j{\cos }^2\beta ={\omega }_{j+1}+\Omega {\text{'}}_j{\cos }^2\beta }$

• Conservación de la energía

En un choque elástico se iguala la energía del sistema antes y después del choque. Se trata de energía cinética de rotación

${\displaystyle \frac{1}{2}\left(m{l}^2\right){\Omega }_j^2=\frac{1}{2}\left(m{l}^2\right){\omega }_{j+1}^2+\frac{1}{2}\left(m{l}^2\right)\Omega {\text{'}}_j^2}$

Eliminamos Ω'_j del sistema de dos ecuaciones

${\displaystyle {\omega }_{j+1}=\frac{2{\cos }^2\beta }{1+{\cos }^4\beta }{\Omega }_j}$

Movimiento de caída

Aplicamos el principio de conservación de la energía para calcular la velocidad angular Ω_j de la varilla A_j inmediatamente antes del choque

${\displaystyle \begin{array}{l}\frac{1}{2}\left(m{l}^2\right){\omega }_j^2+mgl=\frac{1}{2}\left(m{l}^2\right){\Omega }_j^2+mgl\cos \beta \\ {\Omega }_j^2={\omega }_j^2+4\frac{g}{l}{\sin }^2\left(\frac{\beta }{2}\right)\end{array}}$

Relación de recurrencia

La relación de recurrencia entre las velocidades angulares ω_j y ω_j+1 es

${\displaystyle \begin{array}{l}{\omega }_{j+1}^2={\left(\frac{2{\cos }^2\beta }{1+{\cos }^4\beta }\right)}^2\left({\omega }_j^2+4\frac{g}{l}{\sin }^2\left(\frac{\beta }{2}\right)\right)\\ {\omega }_{j+1}^2=f^2{\omega }_j^2+b\end{array}}$

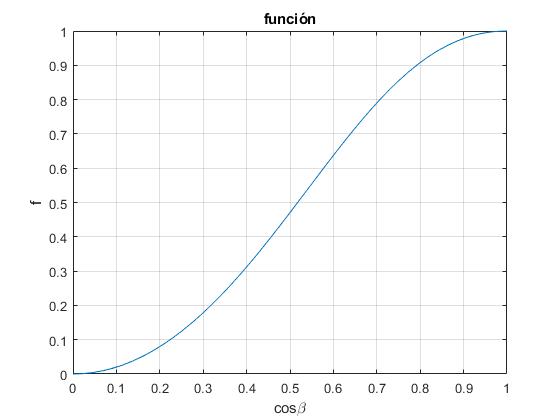
f es un parámetro menor que la unidad, como puede apreciarse en la representación gráfica, donde la variable x representa cosβ

f=@(x) 2*(x.^2)./(1+x.^4);
fplot(f,[0,1])
grid on
xlabel('cos\beta')
ylabel('f')
title('función')

Tenemos una progresión de la forma a_j+1=r·a_j+b. Por ejemplo

a₂=r·a₁+b
a₃=r·a₂+b
a₄=r·a₃+b
a₅=r·a₄+b
.....

Despejamos a₅ en función de a₁. a₅=r⁴a₁+b(r³+r²+r+1)

${\displaystyle a_{j+1}=r^j{a}_1+b{\displaystyle \sum _{i=1}^j{r}^{i-1}}}$

El factor que multiplica a b es la suma de j términos de una progresión geométrica de razón r

${\displaystyle a_{j+1}=r^j{a}_1+b\frac{1-r^j}{1-r}}$

La relación de recurrencia se transforma de acuerdo con esta fórmula en

${\displaystyle {\omega }_{j+1}^2=f^{2j}{\omega }_1^2+b\frac{1-f^{2j}}{1-f^2}}$

Tiempo de colisión

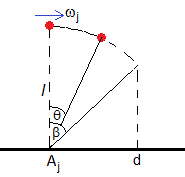
El principio de conservación de la energía nos proporciona el tiempo que tarda la ficha desde que está en posición vertical θ=0 con velocidad ω_j hasta que choca con la adyacente, θ=β con velocidad angular Ω_j.

${\displaystyle \begin{array}{l}\frac{1}{2}\left(m{l}^2\right){\omega }_j^2+mgl=\frac{1}{2}\left(m{l}^2\right){\left(\frac{d\theta }{dt}\right)}^2+mgl\cos \theta \\ {\left(\frac{d\theta }{dt}\right)}^2={\omega }_j^2+2\frac{g}{l}\left(1-\cos \theta \right)\end{array}}$

Despejamos dt en integramos para calcula el tiempo T_j de choque

${\displaystyle {\displaystyle \underset{0}{\overset{T_j}{\int }}dt}={\displaystyle \underset{0}{\overset{\beta }{\int }}\frac{d\theta }{\sqrt{{\omega }_j^2+2\frac{g}{l}\left(1-\cos \theta \right)}}}}$

Es una integral del tipo

${\displaystyle \begin{array}{l}I(\beta )={\displaystyle \underset{0}{\overset{\beta }{\int }}\frac{d\theta }{\sqrt{a-c\cos \theta }},0<c<a}\\ a={\omega }_j^2+2\frac{g}{l},c=2\frac{g}{l}\end{array}}$

Se hace el cambio de variable θ=π-2z, dθ=-2·dz

${\displaystyle \begin{array}{l}I(\beta )=2{\displaystyle \underset{(\pi -\beta )/2}{\overset{\pi /2}{\int }}\frac{dz}{\sqrt{a+c\cos (2z)}}}\\ I(\beta )=2{\displaystyle \underset{(\pi -\beta )/2}{\overset{\pi /2}{\int }}\frac{dz}{\sqrt{(a+c)-2c{\sin }^2(z)}}}\\ I(\beta )=\frac{2}{\sqrt{a+c}}{\displaystyle \underset{(\pi -\beta )/2}{\overset{\pi /2}{\int }}\frac{dz}{\sqrt{1-\frac{2c}{a+c}{\sin }^2(z)}}}=\frac{2}{\sqrt{a+c}}\left\{{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{dz}{\sqrt{1-k^2{\sin }^2(z)}}-{\displaystyle \underset{0}{\overset{(\pi -\beta )/2}{\int }}\frac{dz}{\sqrt{1-k^2{\sin }^2(z)}}}}\right\}\\ I(\beta )=\frac{2}{\sqrt{a+c}}\left\{K(k)-F\left(\frac{\pi -\beta }{2},k\right)\right\}\end{array}}$

El tiempo de choque en términos de integrales elípticas es

${\displaystyle \begin{array}{l}{T}_j=\frac{2}{\sqrt{{\omega }_j^2+4\frac{g}{l}}}\left\{K(k)-F\left(\frac{\pi -\beta }{2},k\right)\right\}\\ k^2=\frac{2c}{a+c}=\frac{4\frac{g}{l}}{{\omega }_j^2+2\frac{g}{l}+2\frac{g}{l}}=\frac{4}{{\omega }_j^2+4\frac{g}{l}}\frac{g}{l}\\ \sin \beta =\frac{d}{l}\end{array}}$

La velocidad de propagación es

Ejemplo

Consideremos fichas dispuestas verticalmente, de altura l=5 cm, separadas d=3 cm

Calculamos y representamos la velocidad de propagación v_j en función de j=1,2,3...50

L=0.05; %longitud
d=0.03; %separación
beta=asin(d/L);
w0=1; %velocidad angular inicial
f2=2*cos(beta)^2/(1+cos(beta)^4);
b=f2*4*9.8*sin(beta/2)^2/L;
n=50;
T=zeros(1,n); %tiempos
for j=1:n
    w2=f2^(j-1)*w0+b*((1-f2^(j-1))/(1-f2));
    k2=4*(9.8/L)/(w2+4*9.8/L);
    T(j)=2*(ellipke(k2)-ellipticF((pi-beta)/2,k2))/sqrt(w2+4*9.8/L);
end
plot(1:n,d./T,'o','markersize',3,'markeredgecoLor','r','markerfacecoLor','r')
xlabel('j')
ylabel('v_j')
grid on
title('Velocidad')

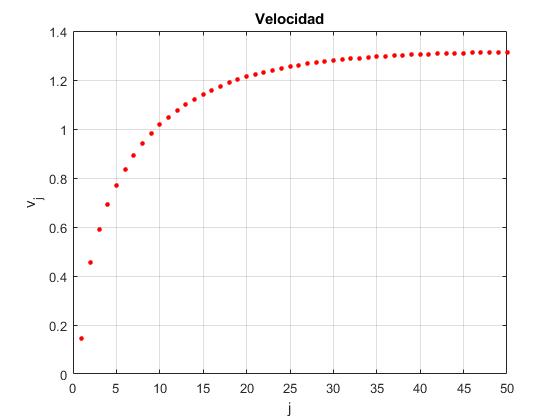
La velocidad de propagación tiende hacia un valor constante, de aproximadamente

>> d/T(end)
ans =    1.3132

que es independiente de la velocidad angular inicial, ω₀ que se imparte a la primera ficha

Referencias

C. J. Efthimiou. M. D. Johnson. Domino Waves. SIAM REVIEW 2007. Society for Industrial and Applied Mathematics. Vol. 49, No. 1, pp. 111–120. https://epubs.siam.org/doi/abs/10.1137/S0036144504414505?journalCode=siread

J. M. J. van Leeuwen. The domino effect. Am. J. Phys. 78 (7), July 2010, pp. 721-727