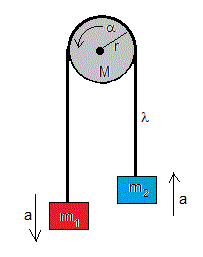
La cuerda tiene longitud L y densidad λ. Los bloques que cuelgan de los extremos de la cuerda tienen masas m₁ y m₂, supondremos que el bloque de masa m₁ desciende con aceleración a y el bloque de masa m₂ asciende con la misma aceleración. El disco de masa M y radio R, gira con velocidad angular α en el sentido indicado, no consideraremos el rozamiento en el eje.

Ecuaciones del movimiento

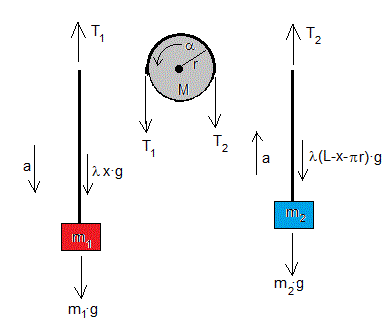
Analizamos el movimiento del sistema formado por el bloque de masa m₁ y la parte izquierda de la cuerda de longitud x.

El momento lineal es p=(λ·x+m₁)·v, siendo v=dx/dt la velocidad de este bloque y porción de cuerda

La resultante de las fuerzas que actúan sobre el sistema es F=m₁g+λ·g·x-T₁

La definición de fuerza dp/dt=F, se escribe para este sistema de masa variable.

${\displaystyle \begin{array}{l}\frac{d\left(\left(\lambda x+m_1\right)v\right)}{dt}=m_{1}g+\lambda xg-T_1\\ \left(\lambda x+m_1\right)\frac{d^{2}x}{d{t}^2}+\lambda {\left(\frac{dx}{dt}\right)}^2=m_{1}g+\lambda xg-T_1\end{array}}$

Analizamos el movimiento del sistema formado por el bloque de masa m₂ y la parte derecha de la cuerda de longitud (L-πr-x). πr es la porción de cuerda que gira con el disco

El momento lineal es p=(λ(L-πr-x)+m₂)·v, siendo v=dx/dt la velocidad de este bloque y porción de cuerda

La resultante de las fuerzas que actúan sobre el sistema es F=T₂-m₂g-λ(L-πr-x)·g

${\displaystyle \begin{array}{l}\frac{d\left(\left(\lambda (L-\pi r-x)+m_2\right)v\right)}{dt}=T_2-m_{2}g-\lambda (L-\pi r-x)g\\ \left(\lambda (L-\pi r-x)+m_2\right)\frac{d^{2}x}{d{t}^2}-\lambda {\left(\frac{dx}{dt}\right)}^2=T_2-m_{2}g-\lambda (L-\pi r-x)g\end{array}}$

El momento de inercia del disco y la porción de cuerda πr que gira solidaria con el disco es

${\displaystyle I=\frac{1}{2}M{r}^2+\lambda \pi r·r^2=\left(\frac{1}{2}M+\lambda \pi r\right)r^2}$

Escribimos la ecuación de la dinámica de rotación y la relación entre la aceleración a de los bloques y la aceleración angular α del disco.

${\displaystyle \begin{array}{l}I\alpha =T_{1}r-T_{2}r\\ a=\alpha ·r\end{array}}$

En el sistema de tres ecuaciones eliminamos T₁ y T₂, despejando la aceleración a de los bloques

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{m_1-m_2-\lambda L+\lambda \pi r+2\lambda x}{m_1+m_2+M/2+\lambda L}g\\ \frac{d^{2}x}{d{t}^2}=Ax+B\\ A=\frac{2\lambda }{m_1+m_2+M/2+\lambda L}gB=\frac{m_1-m_2-\lambda (L-\pi r)}{m_1+m_2+M/2+\lambda L}g\end{array}}$

Cuando x=0, y dx/dt=0, la aceleración debe de ser positiva para que se incremente x, es decir B tiene que ser positivo, lo que implica que m₁>m₂+λ(L-πr)

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}x=C\exp \left(\sqrt{A}t\right)+D\exp \left(-\sqrt{A}t\right)-\frac{B}{A}\\ \frac{dx}{dt}=\sqrt{A}\left(C\exp \left(\sqrt{A}t\right)-D\exp \left(-\sqrt{A}t\right)\right)\end{array}}$

Donde C y D se determinan a partir de las condiciones iniciales, en el instante t=0, el bloque de masa m₁ parte de la posición x₀, con velocidad dx/dt=0

${\displaystyle \begin{array}{l}{x}_0=C+D-\frac{B}{A}\\ 0=\sqrt{A}\left(C-D\right)\end{array}\}C=\frac{1}{2}\left(x_0+\frac{B}{A}\right)D=\frac{1}{2}\left(x_0+\frac{B}{A}\right)}$

La posición x y velocidad v del bloque de masa m₁ en función del tiempo t es

${\displaystyle \begin{array}{l}x=\left(x_0+\frac{B}{A}\right)\left(\cosh \left(\sqrt{A}t\right)\right)-\frac{B}{A}\\ \frac{dx}{dt}=\sqrt{A}\left(x_0+\frac{B}{A}\right)\left(\sinh \left(\sqrt{A}t\right)\right)\end{array}}$

Energía

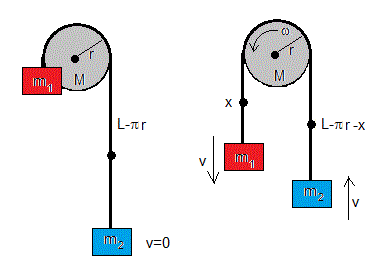
Establecemos el nivel cero de energía potencial a la altura del eje de la polea y comparamos la situación inicial (a la izquierda) con la situación final a la derecha. El punto de color negro, señala el centro de masa de la cuerda que cuelga por ambos lados de la polea.

${\displaystyle \begin{array}{l}{E}_i=-m_{2}g(L-\pi r)-\lambda (L-\pi r)g\frac{(L-\pi r)}{2}\\ E_f=-m_{2}g(L-\pi r-x)-\lambda (L-\pi r-x)g\frac{(L-\pi r-x)}{2}-\lambda xg\frac{x}{2}-m_{1}gx+\\ \frac{1}{2}{m}_2{v}^2+\frac{1}{2}{m}_1{v}^2+\frac{1}{2}(\lambda L)v^2+\frac{1}{2}\left(\frac{1}{2}M{r}^2\right){\omega }^2\end{array}}$

Teniendo en cuenta v=ωr, y que la energía inicial E_i es igual a la final, E_f, simplificamos y despejamos la velocidad v en función de la posición x del bloque de masa m₁.

${\displaystyle \begin{array}{l}{v}^2=\frac{m_1-m_2-\lambda (L-\pi r-x)}{m_1+m_2+\lambda L+M/2}2gx\\ v=\sqrt{A{x}^2+2Bx}\end{array}}$

Cuando x=0, v²>0 siempre que m₁>m₂+λ(L-πr)

m1=300; %masa del primer bloque en g
m2=200; %masa del segundo eng
r=30;   %radio polea en cm
L=140+pi*r; %longitud de la cuerda en cm
lambda=0.15;  %densidad g/cm
M=100;  %masa polea
 
A=2*lambda*100/(m1+m2+M/2+lambda*L); %*100 para expresar x en m
B=(m1-m2-lambda*L+lambda*pi*r)*9.8/(m1+m2+M/2+lambda*L);
 
v=@(x) sqrt(A*x^2+2*B*x);
fplot(v,[0,1.4])
grid on
xlabel('x')
ylabel('v')
title('Máquina de Atwood')

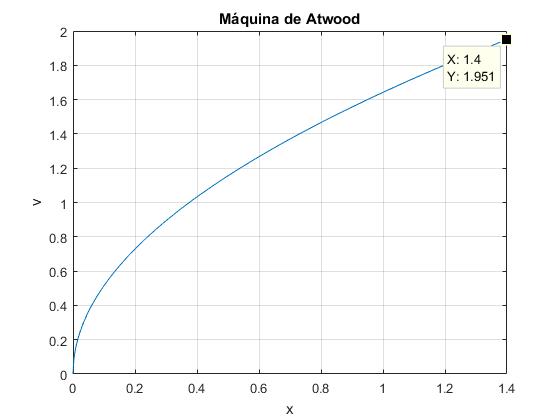
Como v=dx/dt, integramos para obtener por otro método la posición x en función del tiempo t

${\displaystyle {\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{\sqrt{A{x}^2+2Bx}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}}$

Donde A y B son las constantes que hemos definido anteriormente.

Se hace el cambio u=Ax/B+1, y a continuación u=coshθ. Se deshacen los cambios y se obtiene

${\displaystyle x=\frac{B}{A}\left(\cosh \left(\sqrt{A}t\right)-1\right)}$

El mismo resultado, pero con más trabajo en el proceso de integración

Ecuaciones de Lagrange

La energía final E_f contiene la suma de la energía cinética T y potencial V del sistema en función de x y v=dx/dt. Agrupando términos, escribimos la Lagrangiana L=T-V

${\displaystyle \begin{array}{l}L=\frac{1}{2}\left(m_2+m_1+\lambda L+\frac{1}{2}M\right){\left(\frac{dx}{dt}\right)}^2\\ +m_{2}g(L-\pi r-x)+\lambda (L-\pi r-x)g\frac{(L-\pi r-x)}{2}+\lambda xg\frac{x}{2}+m_{1}gx\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\left(\frac{\partial L}{\partial x}\right)=0\\ \left(m_2+m_1+\lambda L+\frac{1}{2}M\right)\frac{d^{2}x}{d{t}^2}+m_{2}g+\lambda (L-\pi r-x)g-\lambda xg-m_{1}g=0\\ \frac{d^{2}x}{d{t}^2}=\frac{m_1-m_2-\lambda (L-\pi r)+2\lambda x}{m_2+m_1+\lambda L+\frac{1}{2}M}g\end{array}}$

Obtenemos la misma ecuación del movimiento

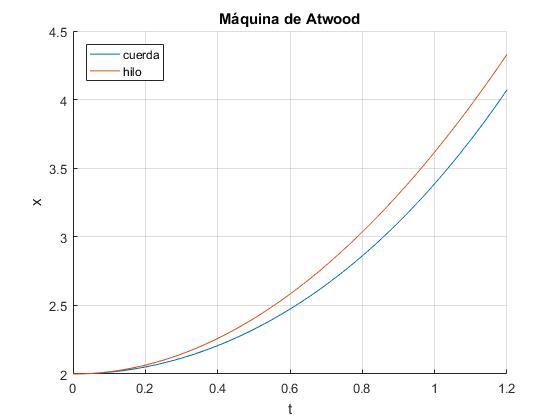
En el segundo artículo citado en las referencias, se proporciona el siguiente ejemplo: densidad de la cuerda λ=0.02 kg/m, radio de la polea r=2.5 cm, masa de la polea M=1.76 g, pesas que cuegan de masas m₁=0.2 kg y m₂=0.1 kg. La longitud de la cuerda es L=4+πr m. Comparamos el movimiento del sistema con esta cuerda y con un hilo, supuesto inextensible y sin masa. En este último caso, la aceleración vale

${\displaystyle a=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g}$

m1=0.2; %pesas que cuelgan
m2=0.1;
M=5.76e-3; %masa polea
r=0.025; %radio polea
lambda=0.02; %densidad cuerda
L=4+pi*r; %longitud cuerda
A=2*lambda*9.8/(m1+m2+M/2+lambda*L);
B=(m1-m2-lambda*(L-pi*r))*9.8/(m1+m2+M/2+lambda*L);


x0=2;
hold on
x=@(t) (x0+B/A)*cosh(sqrt(A)*t)-B/A;
xx=@(t) x0+(m1-m2)*9.8*t.^2/(2*(m1+m2+M/2));
fplot(x,[0,1.2])
fplot(xx,[0,1.2])
hold off
grid on
legend('cuerda','hilo', 'location','northwest')
xlabel('t')
ylabel('x')
title('Máquina de Atwood')

>> A
A =    1.0196
>> B
B =    0.5098

Actividades

Se introduce

• La masa m₁, del bloque de color azul, en el control titulado Masa m₁
• La masa m₂, del bloque de color rojo, en el control titulado Masa m₂
• La densidad de la cuerda λ, en el control titulado Densidad
• Se ha fijado el radio de la polea, R=30 cm la masa M=100g de la polea y la longitud de la cuerda L=1.4+π·0.3

Se pulsa el botón titulado Nuevo, se observa el movimiento de los bloques y la polea.

En el caso de que no se cumpla la condición m₁>m₂+λ(L-πr). El programa no prosigue y nos invita a incrementar la masa del bloque azul m₁ o disminuir la masa del bloque rojo, m₂ o la densidad λ de la cuerda.

Referencias

Mariusz Tarnopolski. On Atwood's Machine with Nonzero Mass String. The Physics Teacher, Vol 53, November 2015, pp. 494-496

Nivaldo A Lemos. Atwood's machine with a massive string. Eur. J. Phys. 38 (2017) 065001