Escalera apoyada en dos paredes perpendiculares. La vertical es lisa

Estática

Para resolver el problema supondremos que F_y=0, en la pared vertical no hay rozamiento.

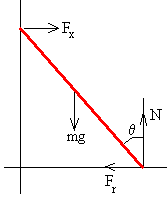
Cuando la escalera forma un ángulo θ con la vertical las ecuaciones de equilibrio son:

1. La resultante de la fuerzas debe ser cero.

${\displaystyle \begin{array}{l}{F}_x=F_r\\ N=mg\end{array}}$

2. El momento de las fuerzas respecto de cualquier punto (por ejemplo el extremo inferior de la escalera) es cero.

${\displaystyle -F_{x}L\cos \theta +mg\frac{L}{2}\sin \theta =0}$

Conocido el ángulo θ, despejamos la fuerza de rozamiento F_r que impide que el extremo inferior deslice a lo largo de la pared horizontal

${\displaystyle F_r=\frac{mg}{2}\tan \theta }$

A medida que se incrementa el ángulo θ, se inclina cada vez más la escalera, la fuerza de rozamiento aumenta. Alcanza su valor máximo cuando

F_r=μ_sN= μ_smg

Donde μ_s es el coeficiente estático

El ángulo límite θ_s a partir del cual la escalera empieza a deslizar es

tanθ_s=2μ_s

Dinámica

Si el ángulo que forma la escalera es mayor que el límite, θ₀>θ_s la escalera empieza a deslizar. La fuerza de rozamiento F_r=μN en el extremo inferior de la escalera disminuye ligeramente, ya que el coeficiente cinético μ suele ser menor que el estático μ_s

El movimiento de la escalera consta de dos etapas:

El extremo superior de la escalera permanece en contacto con la pared vertical

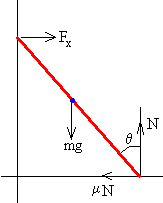
• Movimiento de traslación del cm.

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=F_x-\mu N\hfill \\ m\frac{d^{2}y}{d{t}^2}=N-mg\hfill \end{array}}$

• Movimiento de rotación alrededor de un eje perpendicular al plano de la escalera que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{L}{2}\sin \theta -F_x\frac{L}{2}\cos \theta -\mu N\frac{L}{2}\cos \theta }$

con I_c=mL²/12, se supone que la escalera es una varilla homogénea de masa m y longitud L

La posición del centro de masas es (x, y). Mientras el extremo superior de la escalera está apoyado en la pared vertical F_x>0, hay una relación entre x, y y el ángulo θ.

${\displaystyle x=\frac{L}{2}\sin \theta y=\frac{L}{2}\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{L}{2}\cos \theta \frac{d\theta }{dt}\\ \frac{d^{2}x}{d{t}^2}=\frac{L}{2}\left\{-\text{sin}\theta {\left(\frac{d\theta }{dt}\right)}^2+\cos \theta \frac{d^2\theta }{d{t}^2}\right\}\\ \frac{dy}{dt}=-\frac{L}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Despejamos F_x y N en las ecuaciones del movimiento del c.m.

${\displaystyle \begin{array}{l}N=mg-m\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\\ F_x=\mu mg+m\frac{L}{2}\left\{\frac{d^2\theta }{d{t}^2}\left(\cos \theta -\mu \text{sin}\theta \right)-{\left(\frac{d\theta }{dt}\right)}^2\left(\text{sin}\theta +\mu \cos \theta \right)\right\}\end{array}}$

Introducimos N, F_x y F_r=μN en la ecuación de la dinámica de rotación.

${\displaystyle \left(\frac{2}{3}-\mu \sin \theta \cos \theta \right)\frac{d^2\theta }{d{t}^2}=\frac{g}{L}\left(\sin \theta -2\mu \cos \theta \right)+\mu {\cos }^2\theta {\left(\frac{d\theta }{dt}\right)}^2}$

El mismo resultado que obtuvimos en la página titulada Escalera apoyada en dos paredes perpendiculares con μ_B=0

Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: En el instante t=0, dθ/dt=0, θ=θ₀.

Sea una escalera de longitud L=1 m, el coeficiente de rozamiento μ=0.3 entre en el apoyo de la escalera en el suelo, el ángulo inicial θ₀=35°>θ_s=30.9°. Resolvemos la ecuación diferencial del movimiento, utilizando la función ode45 de MATLAB, interrumpimos el proceso de integración cuando la escalera llega al suelo θ=π/2

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Representamos la reacción F_x en la pared vertical en función del ángulo θ

L=1; %longitud de la escalera
th_0=35*pi/180; %ángulo inicial
mu=0.3; %coeficiente de rozamiento

f=@(t,x) [x(2);(9.8*(sin(x(1))-2*mu*cos(x(1)))/L+mu*cos(x(1))^2*x(2)^2)
/(2/3-mu*sin(x(1))*cos(x(1)))]; 
opts=odeset('events',@stop_escalera_1);
[t,x]=ode45(f,[0,1],[th_0,0],opts);
acel=(9.8*(sin(x(:,1))-2*mu*cos(x(:,1)))/L+mu*(cos(x(:,1)).^2).*(x(:,2).^2)).
/(2/3-mu*sin(x(:,1)).*cos(x(:,1)));
Fx=mu*9.8+L*((cos(x(:,1))-mu*sin(x(:,1))).*acel-(sin(x(:,1))+mu*cos(x(:,1))).
*(x(:,2).^2))/2;
plot(x(:,1), Fx);
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
ylabel('F_x')
xlabel('\theta')
title('Escalera, con rozamiento en el suelo')

Observamos que la fuerza horizontal que ejerce la pared vertical F_x va disminuyendo hasta que se hace cero en el instante t_l. El ángulo que forma la escalera con la vertical es θ_l

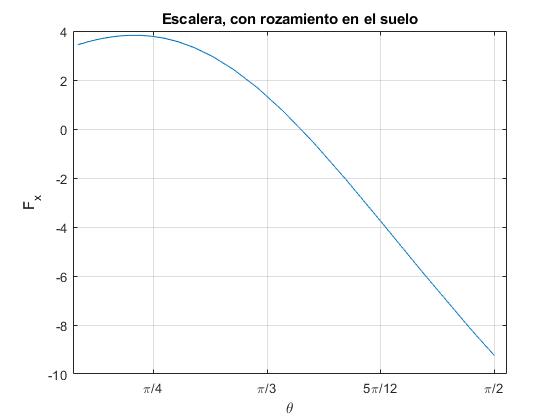
La reacción F_x se hace cero para θ_l=65° aproximadamente. Para este ángulo la velocidad angular de rotación es (dθ/dt)_l. La velocidad horizontal del centro de masas es

${\displaystyle {\left(\frac{dx}{dt}\right)}_l=\frac{L}{2}\cos {\theta }_l{\left(\frac{d\theta }{dt}\right)}_l}$

que son las velocidades iniciales para la segunda etapa del movimiento

El extremo superior de la escalera deja de estar en contacto con la pared vertical

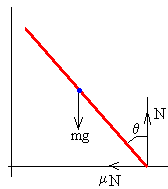
Las ecuaciones del movimiento son

• Movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\mu N\\ m\frac{d^{2}y}{d{t}^2}=N-mg\end{array}}$

• Movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{L}{2}\text{sin}\theta -\mu N\frac{L}{2}\cos \theta }$

La ordenada y del centro de masas es

${\displaystyle y=\frac{L}{2}\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dy}{dt}=-\frac{L}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Despejamos la reacción N

${\displaystyle N=mg-m\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}}$

Introducimos la expresión de N en la ecuación de la dinámica de rotación y en la de traslación del c.m. Obtenemos el sistema de dos ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\mu g-\mu \frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\sin \theta \frac{d^2\theta }{d{t}^2}\right\}\\ \left(\frac{1}{3}+\sin \theta (\sin \theta -\mu \cos \theta )\right)\frac{d^2\theta }{d{t}^2}=\left(2\frac{g}{L}-\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\right)(\sin \theta -\mu \cos \theta )\end{array}}$

El mismo resultado que obtuvimos en la página titulada Escalera apoyada en dos paredes perpendiculares con μ_A=μ

Movimiento completo

El movimiento de la escalera desde la posición inicial θ₀>θ_s hasta la posición final π/2, se describe mediante ecuaciones diferenciales de segundo orden:

• la primera, en el intervalo (θ₀, θ_l)

${\displaystyle \frac{d^2\theta }{d{t}^2}=f\left(\theta ,\frac{d\theta }{dt}\right)}$

• la segunda, en el intervalo (θ_l, π/2)

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=g\left(\theta ,\frac{d\theta }{dt}\right)\\ \frac{d^2\theta }{d{t}^2}=h\left(\theta ,\frac{d\theta }{dt}\right)\end{array}}$

Definimos dos funciones: una función que detenga el primer proceso de integración cuando se alcance el ángulo θ_l y de comienzo al segundo proceso de integración y otra que detenga la integración para el ángulo π/2

function [value,isterminal,direction]=stop_escalera_2(t,x, mu, L)
    acel=3*(9.8*((1-mu^2)*sin(x(1))-2*mu*cos(x(1)))/L+mu*x(2)^2)/(2-mu^2);
    N_B=mu*9.8/(1+mu^2)+L*((cos(x(1))-mu*sin(x(1)))*acel-(sin(x(1))+
mu*cos(x(1)))*x(2)^2)/(2*(1+mu^2));
    value=N_B;  
    isterminal=1;
    direction=-1; 
end

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Consideremos una escalera de longitud L=1, que se suelta cuando forma un ángulo θ₀=35° con la vertical. Representamos el ángulo θ que hace la escalera con la dirección vertical en función del tiempo t

L=1; %longitud de la escalera+
mu=0.3; %empieza a deslizar con 31º
th_0=35*pi/180; %ángulo inicial

f=@(t,x) [x(2);(9.8*(sin(x(1))-2*mu*cos(x(1)))/L+mu*cos(x(1))^2*x(2)^2)
/(2/3-mu*sin(x(1))*cos(x(1)))]; 
opts=odeset('events',@(t,x) stop_escalera_2(t,x, mu,L));
[t,x]=ode45(f,[0,10],[th_0,0],opts);
hold on
plot(t,x(:,1));
tL=t(end);
disp([tL,x(end,1)*180/pi])
opts=odeset('events',@stop_escalera_1);
f=@(t,x) [x(2);(sin(x(1))-mu*cos(x(1)))*(2*9.8/L-cos(x(1))*x(2)^2)
/(1/3+(sin(x(1))-mu*cos(x(1)))*sin(x(1)))]; 
[t,x]=ode45(f,[0,10],[x(end,1),x(end,2)],opts);
plot(t+tL,x(:,1))

hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('t')
ylabel('\theta')
title('Escalera, con rozamiento en el suelo')

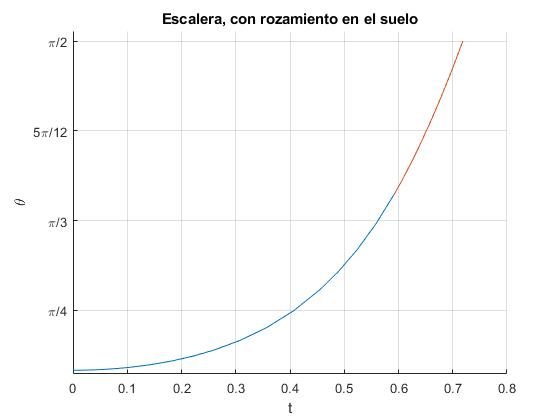
La primera etapa del movimiento se representa en color azul, la segunda, cuando la escalera ya no se apoya en la pared vertical, en rojo. El instante t_l, el ángulo θ_l y el tiempo en llegar al suelo son

       0.5925   64.4647
 >> tL+t(end) %en el suelo
ans =    0.7186

Actividades

Se introduce

• El ángulo θ₀ que forma la escalera con la vertical, en el control titulado Ángulo
• El coeficiente de rozamiento μ_s=μ_k=μ, en el control titulado Coef. rozamiento.
• Se han fijado la longitud de la escalera en L=1 m y la masa m=1 kg

Se pulsa el botón titulado Nuevo

Si el ángulo θ₀ es menor que el ángulo límite tanθ_s=2μ_s

• La escalera permanece en equilibrio

• En caso contrario, observamos el movimiento de la escalera y las fuerzas sobre la misma.

El programa interactivo nos suministra los datos del tiempo t, el ángulo θ que forma la escalera con la dirección vertical, las reacciones F_x en el apoyo en la pared vertical y N en el apoyo en el suelo

Cuando la escalera empieza a deslizar, nos fijaremos en la reacción F_x en el apoyo con la pared vertical, actuando en el botón paso a paso >| medimos el instante t_l y el ángulo θ_l en el que F_x=0, la escalera deja de estar en contacto con la pared vertical.

Una persona sube por la escalera

Supongamos una escalera de longitud L y masa m apoyada en un suelo rugoso y en una pared lisa (sin rozamiento). Un hombre de masa M asciende una distancia d a lo largo de la escalera

Estática

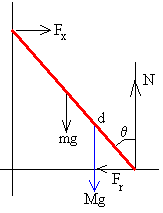
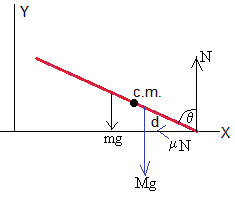
Las fuerzas sobre la escalera son las que se dibujan en la figura.

• F_x es la reacción de la pared vertical supuesta lisa (sin rozamiento)
• N es la  fuerza que ejerce la pared horizontal
• mg es el peso que actúa en el centro de masas de la escalera
• Mg es el peso del hombre.
• F_r es la fuerza de rozamiento que impide que el extremo inferior de la escalera deslice

Cuando la escalera forma un ángulo θ con la vertical las ecuaciones de equilibrio son:

La resultante de la fuerzas debe ser cero.

${\displaystyle \begin{array}{l}{F}_x=F_r\\ N=mg+Mg\end{array}}$

El momento de las fuerzas respecto de cualquier punto (por ejemplo el extremo inferior de la escalera) es cero.

${\displaystyle -F_{x}L\cos \theta +mg\frac{L}{2}\text{sin}\theta +Mgd\text{sin}\theta =0}$

Conocido el ángulo θ y la distancia d que asciende a lo largo de la escalera, despejamos la fuerza de rozamiento F_r que sujeta el extremo inferior de la escalera.

${\displaystyle F_r=\frac{mL/2+Md}{L}g\tan \theta }$

La escalera desliza si

F_r≥μ_sN= μ_s(mg+Mg)

Donde μ_s es el coeficiente estático de rozamiento

La máxima distancia d_m que puede ascender por la escalera, justo en el momento en el que empieza a deslizar, es

${\displaystyle \begin{array}{l}{\mu }_s(mg+Mg)=\frac{mL/2+M{d}_m}{L}g\tan \theta \\ d_m=\left(\frac{{\mu }_s}{\tan \theta }\left(1+\frac{m}{M}\right)-\frac{m}{2M}\right)L\end{array}}$

Dinámica

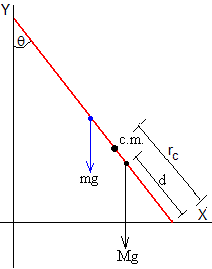
La posición del centro de masas del sistema formado por el hombre y la escalera se encuentra a una distancia r_c medida desde el extremo inferior de la escalera

${\displaystyle r_c=\frac{Md+mL/2}{m+M}}$

Aplicando el teorema de Steiner calculamos el momento de inercia del sistema respecto de un eje que pasa por el centro de masas

${\displaystyle I_c=\frac{1}{12}m{L}^2+m{\left(\frac{L}{2}-r_c\right)}^2+M{\left(r_c-d\right)}^2}$

La fuerza de rozamiento F_r=μN en el extremo inferior de la escalera disminuye ligeramente, ya que el coeficiente cinético μ suele ser menor que el estático μ_s

El movimiento de la escalera consta de dos etapas:

El extremo superior de la escalera permanece en contacto con la pared vertical

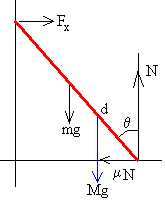
Movimiento de traslación del c.m.

${\displaystyle \begin{array}{l}(m+M)\frac{d^{2}x}{d{t}^2}=F_x-\mu N\\ (m+M)\frac{d^{2}y}{d{t}^2}=N-mg-Mg\end{array}}$

Movimiento de rotación alrededor de un eje que pasa por el centro de masas

$$\begin{gathered} {\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=N{r}_c\text{sin}\theta -F_x(L-r_c)\cos \theta -\mu N{r}_c\cos \theta +mg\left(\frac{L}{2}-r_c\right)\text{sin}\theta - \\ Mg(r_c-d)\text{sin}\theta \\ I_c\frac{d^2\theta }{d{t}^2}=(r_c\text{sin}\theta -\mu r_c\cos \theta )N-F_x(L-r_c)\cos \theta +mg\left(\frac{L}{2}-r_c\right)\text{sin}\theta - \\ Mg(r_c-d)\text{sin}\theta \end{array}} \end{gathered}$$

La posición del centro de masas es (x, y). Mientras el extremo superior de la barra está apoyada en la pared vertical F_x>0, hay una relación entre x, y y el ángulo θ.

${\displaystyle x=(L-r_c)\sin \theta y=x_c\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dx}{dt}=(L-r_c)\cos \theta \frac{d\theta }{dt}\hfill \\ \frac{d^{2}x}{d{t}^2}=(L-r_c)\left\{-\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\cos \theta \frac{d^2\theta }{d{t}^2}\right\}\hfill \\ \frac{dy}{dt}=-r_c\sin \theta \frac{d\theta }{dt}\hfill \\ \frac{d^{2}y}{d{t}^2}=-r_c\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\sin \theta \frac{d^2\theta }{d{t}^2}\right\}\hfill \end{array}}$

Despejamos F_x y N en las ecuaciones del movimiento del c.m.

${\displaystyle \begin{array}{l}N=(m+M)g-(m+M)r_c\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\sin \theta \frac{d^2\theta }{d{t}^2}\right\}\hfill \\ F_x=\mu (m+M)g+(m+M)\left\{\begin{array}{l}\left((L-r_c)\cos \theta -\mu r_c\sin \theta \right)\frac{d^2\theta }{d{t}^2}-\\ \left(\mu r_c\cos \theta +(L-r_c)\sin \theta \right){\left(\frac{d\theta }{dt}\right)}^2\end{array}\right\}\hfill \end{array}}$

Introducimos N, F_x en la ecuación de la dinámica de rotación. Obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}A\frac{d^2\theta }{d{t}^2}=B{\left(\frac{d\theta }{dt}\right)}^2+C\hfill \\ A=I_c+(m+M)\left\{r_c^2+\left(L^2-2L{r}_c\right){\cos }^2\theta -\mu L{r}_c\sin \theta \cos \theta \right\}\hfill \\ B=(m+M)L\cos \theta \left\{\mu r_c\cos \theta +(L-2r_c)\sin \theta \right\}\hfill \\ C=\left(m\frac{L}{2}+Md\right)g\sin \theta -\mu (m+M)Lg\cos \theta \hfill \end{array}}$

Cuando M=0, r_c=L/2, I_c=mL²/12. Obtenemos la misma ecuación diferencial que describe el movimiento de la escalera apoyada en las dos paredes perpendiculares

Sea una escalera de L=5 m de longitud y m=10 kg de masa, el coeficiente de rozamiento μ=0.3 entre la escalera y el suelo.

Apoyamos la escalera en la pared vertical, formando un ángulo de θ₀=25°. Una persona de 60 kg sube por la escalera, ascendiendo d=4 m. Comparamos la fuerza de rozamiento F_r con el valor máximo μ(M+m)g y vemos que la escalera desliza

>> Fr=(m*L/2+M*d)*9.8*tan(th_0)/L
Fr =  242.2002
>> (m+M)*9.8*0.3
ans =  205.8000

Resolvemos la ecuación diferencial del movimiento, utilizando la función ode45 de MATLAB, con las siguientes condiciones iniciales: en el instante t=0, dθ/dt=0, θ=θ₀=25°, d=4 m. Interrumpimos el proceso de integración cuando la escalera llega al suelo θ=π/2

L=5; %longitud de la escalera
m=10; %masa de la escalera
M=60; %masa de la persona
mu=0.3; %empieza a deslizar con 31º
th_0=25*pi/180; %ángulo inicial
d=4; % cuando ha ascendido hasta d

rc=(M*d+m*L/2)/(m+M); %centro de masas
Ic=m*L^2/12+m*(L/2-rc)^2+M*(rc-d)^2; %momento de inercia
f=@(t,x) [x(2); ((m+M)*L*cos(x(1))*(mu*rc*cos(x(1))+(L-2*rc)*sin(x(1)))*x(2)^2+
(m*L/2+M*d)*9.8*sin(x(1))-mu*(m+M)*L*9.8*cos(x(1)))/
(Ic+(m+M)*(rc^2+(L^2-2*L*rc)*cos(x(1))^2-mu*L*rc*sin(x(1))*cos(x(1))))]; 
opts=odeset('events',@ stop_escalera_1);
[t,x]=ode45(f,[0,10],[th_0,0],opts);
acel=((m+M)*L*cos(x(:,1)).*(mu*rc*cos(x(:,1))+(L-2*rc)*sin(x(:,1))).*
(x(:,2).^2)+(m*L/2+M*d)*9.8*sin(x(1))-mu*(m+M)*L*9.8*cos(x(1))).
/(Ic+(m+M)*(rc^2+(L^2-2*L*rc)*cos(x(:,1)).^2-mu*L*rc*sin(x(:,1)).*cos(x(:,1))));
Fx=mu*9.8+(((L-rc)*cos(x(:,1))-mu*rc*sin(x(:,1))).*acel-((L-rc)*sin(x(:,1))+
mu*rc*cos(x(:,1))).*(x(:,2).^2));
plot(x(:,1), Fx);
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
ylabel('F_x')
xlabel('\theta')
title('Escalera, con rozamiento en el suelo')

Observamos que la fuerza horizontal que ejerce la pared vertical F_x va disminuyendo hasta que se hace cero en el instante t_l. El ángulo que forma la escalera con la vertical es θ_l y la velocidad angular de rotación es (dθ/dt)_l.

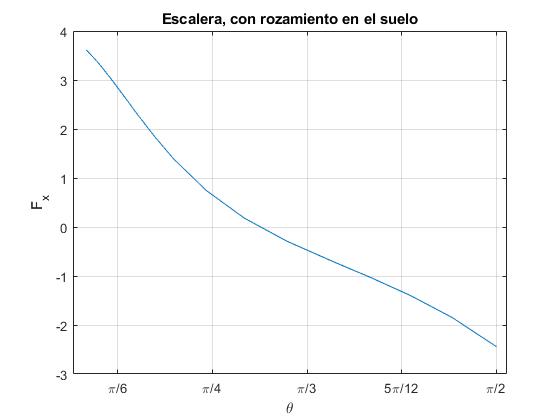
La reacción F_x se hace cero para θ_l=50° aproximadamente. Para este ángulo la velocidad angular de rotación es (dθ/dt)_l. La velocidad horizontal del centro de masas es

${\displaystyle {\left(\frac{dx}{dt}\right)}_l=(L-r_c)\cos {\theta }_l{\left(\frac{d\theta }{dt}\right)}_l}$

El extremo superior de la escalera deja de estar en contacto con la pared vertical

Las ecuaciones del movimiento son

Movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}(m+M)\frac{d^{2}x}{d{t}^2}=-\mu N\hfill \\ (m+M)\frac{d^{2}y}{d{t}^2}=N-mg-Mg\hfill \end{array}}$

Movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N{r}_c\text{sin}\theta -\mu N{r}_c\cos \theta +mg\left(\frac{L}{2}-r_c\right)\text{sin}\theta -Mg(r_c-d)\text{sin}\theta }$

La ordenada y del centro de masas es

${\displaystyle y=r_c\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dy}{dt}=-r_c\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-r_c\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Despejamos la reacción N

${\displaystyle N=(m+M)\left\{g-r_c\cos \theta {\left(\frac{d\theta }{dt}\right)}^2-r_c\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}}$

Introducimos la expresión de N en la ecuación de la dinámica de rotación y en la de traslación del c.m. Obtenemos el sistema de dos ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\mu g+\mu r_c\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\sin \theta \frac{d^2\theta }{d{t}^2}\right\}\hfill \\ A\frac{d^2\theta }{d{t}^2}=B{\left(\frac{d\theta }{dt}\right)}^2+C\hfill \\ A=I_c+(m+M)r_c^2\left(\sin \theta -\mu \cos \theta \right)\sin \theta \hfill \\ B=-(m+M)r_c^2\left(\sin \theta -\mu \cos \theta \right)\cos \theta \hfill \\ C=\left(m\frac{L}{2}+Md\right)g\sin \theta -\mu (m+M)g{r}_c\cos \theta \hfill \end{array}}$

Cuando M=0, r_c=L/2, I_c=mL²/12. Obtenemos la misma ecuación diferencial que describe el movimiento de la escalera apoyada solamente en el suelo

Movimiento completo

El movimiento de la escalera desde la posición inicial θ₀>θ_s hasta la posición final π/2, se describe mediante ecuaciones diferenciales de segundo orden:

• la primera, en el intervalo (θ₀, θ_l)

${\displaystyle \frac{d^2\theta }{d{t}^2}=f\left(\theta ,\frac{d\theta }{dt}\right)}$

• la segunda, en el intervalo (θ_l, π/2)

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=g\left(\theta ,\frac{d\theta }{dt}\right)\\ \frac{d^2\theta }{d{t}^2}=h\left(\theta ,\frac{d\theta }{dt}\right)\end{array}}$

Definimos dos funciones: una función que detenga el primer proceso de integración cuando se alcance el ángulo θ_l y de comienzo al segundo proceso de integración y otra que detenga la integración para el ángulo π/2

function [value,isterminal,direction]=stop_escalera_4(t,x, mu, L,m,M, rc,Ic,d)
    acel=((m+M)*L*cos(x(1))*(mu*rc*cos(x(1))+(L-2*rc)*sin(x(1)))*x(2)^2+
(m*L/2+M*d)*9.8*sin(x(1))-mu*(m+M)*L*9.8*cos(x(1)))/(Ic+(m+M)*
(rc^2+(L^2-2*L*rc)*cos(x(1))^2-mu*L*rc*sin(x(1))*cos(x(1))));
    Fx=mu*9.8+(((L-rc)*cos(x(1))-mu*rc*sin(x(1)))*acel-
((L-rc)*sin(x(1))+mu*rc*cos(x(1)))*x(2)^2);
    value=Fx;  
    isterminal=1;
    direction=-1; 
end

function [value,isterminal,direction]=stop_escalera_1(t,x)
    value=x(1)-pi/2;  
    isterminal=1;
    direction=1; 
end

Sea una escalera de L=5 m de longitud y m=10 kg de masa, el coeficiente de rozamiento μ=0.3 entre la escalera y el suelo. Apoyamos la escalera en la pared vertical, formando un ángulo de θ₀=25°. Una persona de 60 kg sube por la escalera, ascendiendo d=4 m.

L=5; %longitud de la escalera
m=10; %masa de la escalera
M=60; %masa de la persona
mu=0.3; %empieza a deslizar con 31º
th_0=25*pi/180; %ángulo inicial
d=4; % cuando ha ascendido hasta d

rc=(M*d+m*L/2)/(m+M); %centro de masas
Ic=m*L^2/12+m*(L/2-rc)^2+M*(rc-d)^2; %momento de inercia
f=@(t,x) [x(2); ((m+M)*L*cos(x(1))*(mu*rc*cos(x(1))+(L-2*rc)*sin(x(1)))*x(2)^2
+(m*L/2+M*d)*9.8*sin(x(1))-mu*(m+M)*L*9.8*cos(x(1)))/
(Ic+(m+M)*(rc^2+(L^2-2*L*rc)*cos(x(1))^2-mu*L*rc*sin(x(1))*cos(x(1))))]; 
opts=odeset('events',@(t,x) stop_escalera_4(t,x, mu, L,m,M, rc,Ic,d));
[t,x]=ode45(f,[0,10],[th_0,0],opts);
hold on
plot(t,x(:,1));
tL=t(end);
disp([tL,x(end,1)*180/pi])
opts=odeset('events',@stop_escalera_1);
f=@(t,x) [x(2); ((m*L/2+M*d)*9.8*sin(x(1))-mu*(m+M)*9.8*rc*cos(x(1))-
(m+M)*rc^2*(sin(x(1))-mu*cos(x(1)))*cos(x(1))*x(2)^2)
/(Ic+(m+M)*rc^2*(sin(x(1))-mu*cos(x(1)))*sin(x(1)))]; 
[t,x]=ode45(f,[0,10],[x(end,1),x(end,2)],opts);
plot(t+tL,x(:,1))
hold off
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('t')
ylabel('\theta')
title('Escalera, con rozamiento')

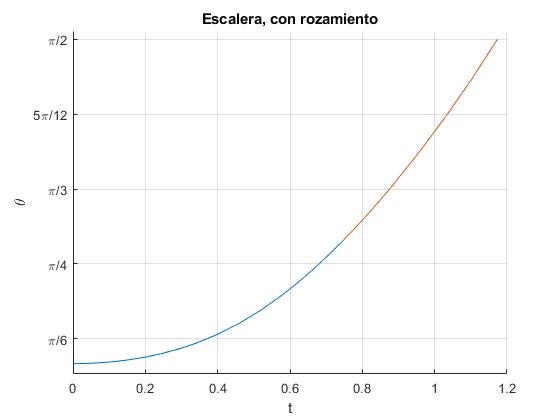
La primera etapa del movimiento se representa en color azul, la segunda, cuando la escalera ya se apoya solamente en el suelo, en rojo. El instante t_l y el ángulo θ_l, y el tiempo total en alcanzar el suelo son

    0.7484   49.7862
>> t(end)+tL
ans =    1.1733

Actividades

Se introduce

• El ángulo θ que forma la escalera con la vertical, en el control titulado Ángulo
• El coeficiente estático y cinético de rozamiento μ_s=μ_k=μ, en el control titulado Coef. rozamiento.
• La masa del hombre M en kg, en el control titulado Masa
• La distacia que asciende d a lo largo de la escalera, en el control titulado Asciende
• Se han fijado la longitud de la escalera en L=5 m y la masa m=10 kg

Se pulsa el botón titulado Nuevo

El sistema formado por la escalera y una masa puntual permanece en equilibrio o se mueve

El programa interactivo nos suministra los datos del tiempo t, el ángulo θ que forma la escalera con la dirección vertical, las reacciones F_x en el apoyo en la pared vertical y N en el apoyo en el suelo

Cuando la escalera empieza a deslizar, nos fijaremos en la reacción F_x en el apoyo con la pared vertical, actuando en el botón paso a paso >| medimos el instante t_l y el ángulo θ_l en el que F_x=0, la escalera deja de estar en contacto con la pared vertical.