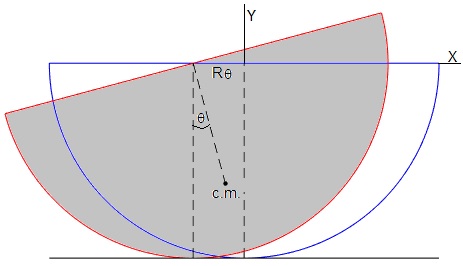
En la figura, se muestra un semicilindro macizo en la posición de equilibrio (en color azul) y su posición en el instante t (en color rojo) cuando ha rodado sin deslizar hacia la izquierda. Ha girado un ángulo θ y su centro se ha desplazado Rθ, siendo R el radio del cilindro

Para dibujar, parte de la figura se ha elaborado el siguiente script

hold on
fplot(@(x) cos(x), @(x) sin(x),[pi,2*pi],'color','b')
line([-1,1],[0,0],'color','b')
line([0,0],[-1,0],'color','k', 'lineStyle','--')
plot(0,-2/pi,'ko','markersize',3,'markeredgecolor','k','markerfacecolor','k')

th=pi/12;
fplot(@(x) cos(x)-th, @(x) sin(x),[pi+th,2*pi+th], 'color','r')
line([-cos(th),cos(th)]-th,[-sin(th),sin(th)],'color','r')
line([-1,1],[-1,-1],'color','k')
line([0,0]-th,[-1,0],'color','k', 'lineStyle','--')

plot(2*sin(th)/pi-th,-2*cos(th)/pi,'ko','markersize',3,
'markeredgecolor','k','markerfacecolor','k')
line([0,2*sin(th)/pi]-th,[0,-2*cos(th)/pi],'color','k', 'lineStyle','--')

hold off
axis equal
axis off

En esta página, vamos a formular las ecuaciones del movimiento, utilizando la ecuación

${\displaystyle \overrightarrow{M_{cm}}=\frac{d\overrightarrow{L_{cm}}}{dt}}$

que es válida incluso si el centro de masas (c.m.) no está en reposo con relación al sistema inercial de referencia

Centro de masas de un cuerpo en forma de semicilindro

Semicilindro hueco

Consideremos una lámina doblada en forma cilíndrica de masa m y radio R. Dicha lámina tiene el mismo centro de masas, que un arco semicircular de radio R

Consideremos un elemento diferencial de arco, comprendido entre θ y θ+dθ, de longitud R·dθ, cuya altura es y=Rsinθ

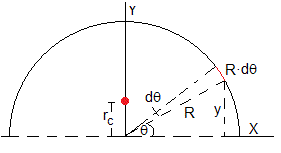
Por simetría, el centro de masas se encuentra en el eje Y, a la altura r_c

${\displaystyle r_c=\frac{{\displaystyle \underset{0}{\overset{\pi }{\int }}y(R·d\theta )}}{{\displaystyle \underset{0}{\overset{\pi }{\int }}R·d\theta }}=\frac{{\displaystyle \underset{0}{\overset{\pi }{\int }}{R}^2\sin \theta ·d\theta }}{{\displaystyle \underset{0}{\overset{\pi }{\int }}R·d\theta }}=\frac{2R}{\pi }}$

Semicilindro macizo

Si el semicilindro es macizo, el centro de masas estará sobre el eje Y a una altura menor. El semicilindro tiene el mismo centro de masas que una lámina semicircular

Tomamos un elemento diferencial de área, un rectángulo horizontal de longitud 2x y anchura dy que se encuentra a una altura y

${\displaystyle r_c=\frac{{\displaystyle \underset{0}{\overset{R}{\int }}y(2x·dy)}}{{\displaystyle \underset{0}{\overset{R}{\int }}2x·dy}}}$

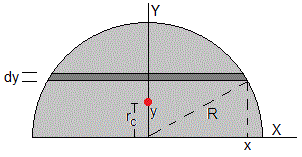
El denominador es el área de un semicírculo πR²/2. Para calcular el numerador, relacionamos las variables x e y a través de la ecuación de la circunferencia, x²+y²=R²

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{R^2-y^2}(2ydy)=}{-\frac{{\left(R^2-y^2\right)}^{3/2}}{\frac{3}{2}}|}_0^R=\frac{2}{3}{R}^3\\ r_c=\frac{\frac{2}{3}{R}^3}{\frac{\pi R^2}{2}}=\frac{4}{3}\frac{R}{\pi }\end{array}}$

Momento de inercia de un cuerpo en forma de semicilindro

Semicilindro hueco

El momento de inercia de una masa m situada a una distancia R del eje de rotación (eje del cilindro)

${\displaystyle I_O=m{R}^2}$

Semicilindro macizo

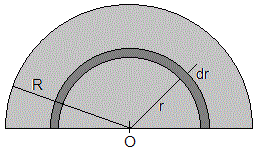
El momento de inercia del semicilindro macizo respecto del eje del cilindro, se calcula de la misma forma que la de un cilindro macizo o un disco, repecto de un eje perpendicular que pasa por el centro

Tomamos un elemento diferencial de área comprendido entre r y r+dr cuya área es (πr)dr

${\displaystyle I_O=\frac{m}{\frac{\pi R^2}{2}}{\displaystyle \underset{0}{\overset{R}{\int }}{r}^2\left(\pi r·dr\right)}=\frac{1}{2}m{R}^2}$

Ecuaciones del movimiento

En la figura, observamos la posición del semicilindro en la situación de equilibrio (en color azul) y en el instante t cuando ha rodado hacia la izquierda. Se ha desplazado Rθ y ha girado un ángulo θ

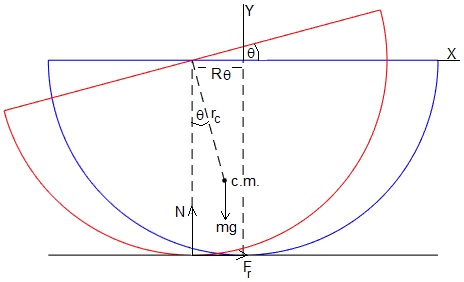
Representamos las fuerzas sobre el semicilindro

• El peso mg en el centro de masas, c.m.
• La reacción N en el punto de contacto con el plano horizontal
• La fuerza de rozamiento F_r en el punto de contacto, para que el semicilindro ruede sin deslizar

Situamos el origen en el centro del semicilindro en equilibrio y los ejes X e Y.

• La posición del centro de masas es

${\displaystyle \{\begin{array}{l}{x}_c=-R\theta +r_c\sin \theta \\ y_c=-r_c\cos \theta \end{array}}$

• La velocidad del centro de masas es

${\displaystyle \{\begin{array}{l}\frac{d{x}_c}{dt}=\left(-R+r_c\cos \theta \right)\frac{d\theta }{dt}\\ \frac{d{y}_c}{dt}=r_c\sin \theta \frac{d\theta }{dt}\end{array}}$

• La aceleración del centro de masas es

${\displaystyle \{\begin{array}{l}\frac{d^2{x}_c}{d{t}^2}=\left(-R+r_c\cos \theta \right)\frac{d^2\theta }{d{t}^2}-r_c\sin \theta {\left(\frac{d\theta }{dt}\right)}^2\\ \frac{d^2{y}_c}{d{t}^2}=r_c\sin \theta \frac{d^2\theta }{d{t}^2}+r_c\cos \theta {\left(\frac{d\theta }{dt}\right)}^2\end{array}}$

Las ecuaciones del movimiento son

• Movimiento de traslación del centro de masas

${\displaystyle \{\begin{array}{l}m\frac{d^2{x}_c}{d{t}^2}=F_r\\ m\frac{d^2{y}_c}{d{t}^2}=N-mg\end{array}}$

• Movimiento de rotación alrededor de un eje perpendicular al plano de la figura, que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=(R-r_c\cos \theta )F_r-(r_c\sin \theta )N}$

Sustituimos F_r y N por sus expresiones en términos de θ y sus derivadas

${\displaystyle \begin{array}{l}{I}_c\frac{d^2\theta }{d{t}^2}=(R-r_c\cos \theta )m\frac{d^2{x}_c}{d{t}^2}-(r_c\sin \theta )\left(m\frac{d^2{y}_c}{d{t}^2}+mg\right)\\ \left(I_c+m\left(R^2+r_c^2-2R{r}_c\cos \theta \right)\right)\frac{d^2\theta }{d{t}^2}+mR{r}_c\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mg{r}_c\sin \theta =0\\ \left(\frac{I_O}{m{R}^2}+1-2\frac{r_c}{R}\cos \theta \right)\frac{d^2\theta }{d{t}^2}+\frac{r_c}{R}\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{R}\frac{r_c}{R}\sin \theta =0\end{array}}$

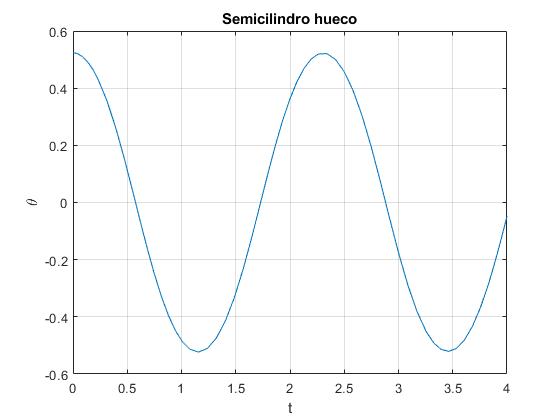
Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, θ=θ₀, dθ/dt=0 (parte del resposo). Para un semicilindro hueco los datos son:

• desplazamiento inicial, θ₀=π/6 (30°)
• posición del centro de masas, r_c=2R/π
• momento de inercia respecto de un eje que pasa por el centro, I_O=mR²

R=1; %radio del semicilindro
rc=2*R/pi; %centro de masas del semicilindro hueco
I0=R^2; %momento de inercia (masa, m=1)
f=@(t,x) [x(2);-(rc*sin(x(1))*x(2)^2/R+9.8*rc*sin(x(1))/R^2)
/(I0/R^2+1-2*rc*cos(x(1))/R)]; 
[t,x]=ode45(f,[0,4],[pi/6,0]);

plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta');
title('Semicilindro hueco')

Conservación de la energía

La energía cinética es la suma de dos términos: la energía cinética del movimiento de traslación del c.m. y la energía cinética del movimiento de rotación alrededor de un eje que pasa por el c.m.

Tomando el origen como nivel cero de energía potencial, la energía potencial del c.m. es -mgr_ccosθ

La energía del semicilindro en el instante t es la suma de ambas contribuciones

${\displaystyle \begin{array}{l}E=\frac{1}{2}m\left({\left(\frac{d{x}_c}{dt}\right)}^2+{\left(\frac{d{y}_c}{dt}\right)}^2\right)+\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2-mg{r}_c\cos \theta \\ E=\frac{1}{2}\left(I_O+m{R}^2-2mR{r}_c\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2-mg{r}_c\cos \theta \end{array}}$

Comprobamos que la energía E/(mR²) se mantiene casi constante

>> E0=-9.8*rc*cos(pi/6)/(R*R)
E0 =   -5.4030
>> E=(I0/(R*R)+1-2*rc*cos(x(:,1))/R).*x(:,2).^2/2-9.8*rc*cos(x(:,1))/(R*R)
E =
   -5.4030
   -5.4030
   -5.4030
...
   -5.4115
   -5.4115

Ecuación de Lagrange

La lagrangiana es

${\displaystyle L=E_k-E_p=\frac{1}{2}\left(I_O+m{R}^2-2mR{r}_c\cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2+mg{r}_c\cos \theta }$

La ecuación diferencial del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d}{dt}\left(\left(I_O+m{R}^2-2mR{r}_c\cos \theta \right)\frac{d\theta }{dt}\right)-mR{r}_c\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mg{r}_c\sin \theta =0\\ \left(I_O+m{R}^2-2mR{r}_c\cos \theta \right)\frac{d^2\theta }{d{t}^2}+2mR{r}_c\sin \theta {\left(\frac{d\theta }{dt}\right)}^2-mR{r}_c\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+mg{r}_c\sin \theta =0\\ \left(\frac{I_O}{m{R}^2}+1-2\frac{r_c}{R}\cos \theta \right)\frac{d^2\theta }{d{t}^2}+\frac{r_c}{R}\sin \theta {\left(\frac{d\theta }{dt}\right)}^2+\frac{g}{R}\frac{r_c}{R}\sin \theta =0\end{array}}$

Actividades

En el programa interactivo, se selecciona un semicilindro hueco o macizo activando el botón de radio correspondiente

La situación inicial del semicilindro en el instante t=0, θ=π/6 (30°), dθ/dt=0 (parte del resposo)

Datos para un semicilindro hueco:

• posición del centro de masas, r_c=2R/π
• momento de inercia respecto de un eje que pasa por el centro, I_O=mR²

Semicilindro macizo:

• posición del centro de masas, r_c=4R/(3π)
• momento de inercia respecto de un eje que pasa por el centro, I_O=mR²/2

En la parte derecha, se proporcionan los datos de

• el tiempo, t
• El desplazamiento angular, θ, que es el ángulo que forma la recta horizontal con el diámetro del semicilindro
• la velocidad angular, dθ/dt
• la posición -Rθ del punto de contacto del cilindro y el plano horizontal

Sabiendo que el máximo desplazamiento angular se produce cuando dθ/dt=0, medimos el periodo de la oscilación utilizando la combinación de botones botones || y >|

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía en cualquier instante t, y E₀=-mgr_ccosθ₀ es la energía inicial del sistema.

Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.

Referencias

Leaf Turner, Ari M. Turner. Asymmetric rolling bodies and the phantom torque. Am. J. Phys. 78 (9) September 2010, pp. 905-907