Sea una placa de momento de inercia I, que puede girar alrededor de un eje con velocidad inicial ω₀. La velocidad angular de rotación ω disminuye con el tiempo a causa del momento M_r de la fuerza de rozamiento. La ecuación del movimiento es

${\displaystyle I\frac{d\omega }{dt}=-M_r}$

Examinamos distintos modelos de rozamiento y sus combinaciones

1. Rozamiento constante

Sea M_r=α·I

Integrando la ecuación del movimiento

${\displaystyle \begin{array}{l}{\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}d\omega }=-\alpha {\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \omega ={\omega }_0-\alpha t\end{array}}$

La velocidad angular disminuye linealmente con el tiempo

2. Rozamiento proporcional a la velocidad angular

Sea M_r=βω·I

Integrando la ecuación del movimiento

${\displaystyle \begin{array}{l}{\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\omega }}=-\beta {\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \ln \omega -\ln {\omega }_0=-\beta t\\ \omega ={\omega }_0\exp \left(-\beta t\right)\end{array}}$

La velocidad angular disminuye exponencialmente con el tiempo

3. Rozamiento proporcional al cuadrado de la velocidad angular

Sea M_r=γω²I

Integrando la ecuación del movimiento

${\displaystyle \begin{array}{l}{\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{{\omega }^2}}=-\gamma {\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{1}{{\omega }_0}-\frac{1}{\omega }=-\gamma t\\ \omega =\frac{{\omega }_0}{1+{\omega }_0\gamma t}\end{array}}$

4. Combinación de rozamiento constante y proporcional a la velocidad angular

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\left(\alpha +\beta \omega \right)\\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\alpha +\beta \omega }}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{1}{\beta }\left(\ln \left(\alpha +\beta \omega \right)-\ln \left(\alpha +\beta {\omega }_0\right)\right)=-t\\ \omega =\left(\frac{\alpha }{\beta }+{\omega }_0\right)\exp \left(-\beta t\right)-\frac{\alpha }{\beta }\end{array}}$

5. Combinación de rozamiento constante y proporcional al cuadrado de la velocidad angular

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\left(\alpha +\gamma {\omega }^2\right)\\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\alpha +\gamma {\omega }^2}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ \frac{1}{\gamma }{\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\frac{\alpha }{\gamma }+{\omega }^2}}=-t\\ \frac{1}{\gamma }\sqrt{\frac{\gamma }{\alpha }}\left\{\arctan \left(\sqrt{\frac{\gamma }{\alpha }}\omega \right)-\arctan \left(\sqrt{\frac{\gamma }{\alpha }}{\omega }_0\right)\right\}=-t\\ \arctan \left(\sqrt{\frac{\gamma }{\alpha }}\omega \right)=\arctan \left(\sqrt{\frac{\gamma }{\alpha }}{\omega }_0\right)-t\sqrt{\alpha \gamma }\end{array}}$

Teniendo en cuenta la relación trigonométrica

${\displaystyle \tan \left(x+y\right)=\frac{\tan x+\tan y}{1-\tan x\tan y}}$

Despejamos la velocidad angular de rotación ω

${\displaystyle \begin{array}{l}\sqrt{\frac{\gamma }{\alpha }}\omega =\frac{\sqrt{\frac{\gamma }{\alpha }}{\omega }_0-\tan \left(t\sqrt{\alpha \gamma }\right)}{1+{\omega }_0\sqrt{\frac{\gamma }{\alpha }}\tan \left(t\sqrt{\alpha \gamma }\right)}\\ \omega =\frac{{\omega }_0-\sqrt{\frac{\alpha }{\gamma }}\tan \left(t\sqrt{\alpha \gamma }\right)}{1+{\omega }_0\sqrt{\frac{\gamma }{\alpha }}\tan \left(t\sqrt{\alpha \gamma }\right)}\end{array}}$

6. Combinación de rozamiento proporcional a la velocidad y proporcional al cuadrado de la velocidad angular

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\left(\beta \omega +\gamma {\omega }^2\right)\\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\beta \omega +\gamma {\omega }^2}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\end{array}}$

Convertimos la fracción en suma de dos fracciones

${\displaystyle \begin{array}{l}\frac{1}{\beta }{\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\left(\frac{1}{\omega }-\frac{\gamma }{\beta +\gamma \omega }\right)d\omega }=-t\\ \frac{1}{\beta }\left\{\ln \frac{\omega }{{\omega }_0}-\ln \frac{\beta +\gamma \omega }{\beta +\gamma {\omega }_0}\right\}=-t\\ \frac{\omega \left(\beta +\gamma {\omega }_0\right)}{{\omega }_0\left(\beta +\gamma \omega \right)}=\exp \left(-\beta t\right)\\ \omega =\frac{\beta {\omega }_0\exp \left(-\beta t\right)}{\beta +\gamma {\omega }_0-\gamma {\omega }_0\exp \left(-\beta t\right)}=\frac{\beta {\omega }_0}{\left(\beta +\gamma {\omega }_0\right)\exp \left(\beta t\right)-\gamma {\omega }_0}\end{array}}$

7. Combinación de rozamiento constante, proporcional a la velocidad y proporcional al cuadrado de la velocidad angular

${\displaystyle \begin{array}{l}\frac{d\omega }{dt}=-\left(\alpha +\beta \omega +\gamma {\omega }^2\right)\\ {\displaystyle \underset{{\omega }_0}{\overset{\omega }{\int }}\frac{d\omega }{\alpha +\beta \omega +\gamma {\omega }^2}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\end{array}}$

Completamos cuadrados

${\displaystyle \alpha +\beta \omega +\gamma {\omega }^2=\alpha -\frac{{\beta }^2}{4\gamma }+{\left(\frac{\beta }{2\sqrt{\gamma }}+\sqrt{\gamma }\omega \right)}^2}$

Efectuamos el cambio de variable

${\displaystyle u=\frac{\beta }{2\sqrt{\gamma }}+\sqrt{\gamma }\omega ,du=\sqrt{\gamma }d\omega }$

La integral es inmediata

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\omega }{\alpha +\beta \omega +\gamma {\omega }^2}=\frac{1}{\sqrt{\gamma }}{\displaystyle \int \frac{du}{\alpha -\frac{{\beta }^2}{4\gamma }+u^2}}}=\frac{1}{\sqrt{\gamma }}\frac{1}{\sqrt{\alpha -\frac{{\beta }^2}{4\gamma }}}\arctan \left(\frac{u}{\sqrt{\alpha -\frac{{\beta }^2}{4\gamma }}}\right)=\\ \frac{2}{\sqrt{4\gamma \alpha -{\beta }^2}}\arctan \left(\frac{\frac{\beta }{2\sqrt{\gamma }}+\sqrt{\gamma }\omega }{\sqrt{\alpha -\frac{{\beta }^2}{4\gamma }}}\right)=\frac{2}{\sqrt{4\gamma \alpha -{\beta }^2}}\arctan \left(\frac{\beta +2\gamma \omega }{\sqrt{4\gamma \alpha -{\beta }^2}}\right)\end{array}}$

La integral definida es

${\displaystyle \begin{array}{l}\frac{2}{\sqrt{4\gamma \alpha -{\beta }^2}}\left\{\arctan \left(\frac{\beta +2\gamma \omega }{\sqrt{4\gamma \alpha -{\beta }^2}}\right)-\arctan \left(\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\right)\right\}=-t\\ \arctan \left(\frac{\beta +2\gamma \omega }{\sqrt{4\gamma \alpha -{\beta }^2}}\right)-\arctan \left(\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\right)=-\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\end{array}}$

Utilizando la fórmula de tan(x+y)

${\displaystyle \begin{array}{l}\arctan \left(\frac{\beta +2\gamma \omega }{\sqrt{4\gamma \alpha -{\beta }^2}}\right)=\arctan \left(\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\right)-\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\\ \frac{\beta +2\gamma \omega }{\sqrt{4\gamma \alpha -{\beta }^2}}=\frac{\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}-\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}{1+\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}\\ \beta +2\gamma \omega =\frac{\beta +2\gamma {\omega }_0-\sqrt{4\gamma \alpha -{\beta }^2}\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}{1+\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}\\ \omega =\frac{{\omega }_0+\frac{\beta }{2\gamma }-\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2\gamma }\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}{1+\frac{\beta +2\gamma {\omega }_0}{\sqrt{4\gamma \alpha -{\beta }^2}}\tan \left(\frac{\sqrt{4\gamma \alpha -{\beta }^2}}{2}t\right)}-\frac{\beta }{2\gamma }\end{array}}$

Cuando β=0, obtenemos la ecuación del modelo 5 (combinación de rozamiento constante y proporcional al cuadrado de la velocidad)

Ejemplo

Sean los coeficientes

• α=0.3
• β=0.1
• γ=0.05

La velocidad inicial de rotacion es ω₀=1 rad/s

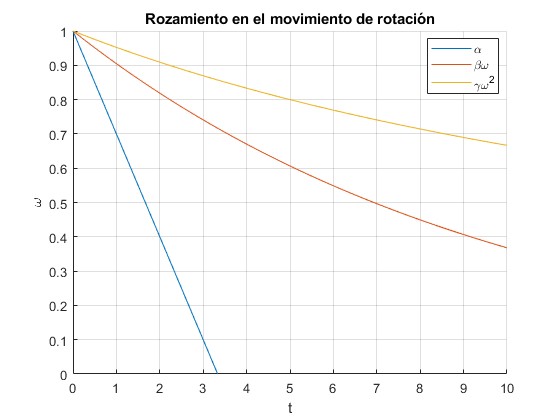
Representamos la velocidad angular ω en función del tiempo para los tres primeros modelos

• Rozamiento constante
• Rozamiento proporcional a la velocidad angular
• Rozamiento proporcional al cuadrado de la velocidad angular

a=0.3;
b=0.1;
c=0.05;

w0=1;
hold on
f=@(t) w0-a*t;
fplot(f,[0,w0/a])
f=@(t) w0*exp(-b*t);
fplot(f,[0,10])
f=@(t) w0./(1+c*w0*t);
fplot(f,[0,10])
hold off
grid on
xlabel('t')
ylabel('\omega')
legend('\alpha','\beta\omega','\gamma\omega^2', 'Location','best')
title('Rozamiento en el movimiento de rotación')

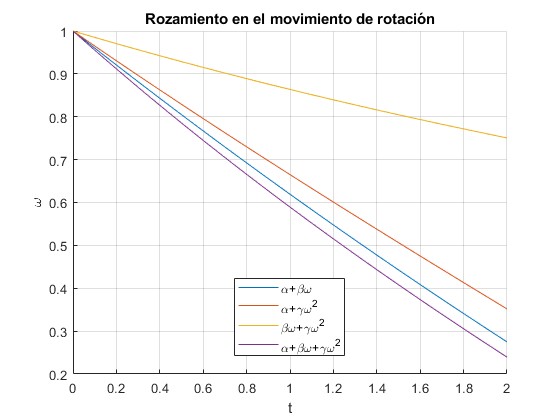
Representamos la velocidad angular ω en función del tiempo para las combinaciones

• de rozamiento constante y proporcional a la velocidad angular
• de rozamiento constante y proporcional al cuadrado de la velocidad angular
• de rozamiento proporcional a la velocidad angular y al cuadrado de la velocidad
• de rozamiento constante, proporcional a la velocidad angular y al cuadrado de la velocidad

a=0.3;
b=0.1;
c=0.05;

w0=1;
hold on
f=@(t) (a/b+w0)*exp(-b*t)-a/b;
fplot(f,[0,2])
f=@(t) (w0-sqrt(a/c)*tan(sqrt(a*c)*t))./(1+w0*sqrt(c/a)*tan(sqrt(a*c)*t));
fplot(f,[0,2])
f=@(t) b*w0./((b+c*w0)*exp(b*t)-c*w0);
fplot(f,[0,2])
f=@(t) (w0+b/(2*c)-sqrt(4*c*a-b^2)*tan(sqrt(4*c*a-b^2)*t/2)/(2*c))./(1+(b+2*c*w0)*
tan(sqrt(4*c*a-b^2)*t/2)/sqrt(4*c*a-b^2))-b/(2*c);
fplot(f,[0,2])

hold off
grid on
xlabel('t')
ylabel('\omega')
legend('\alpha+\beta\omega', '\alpha+\gamma\omega^2','\beta\omega+\gamma\omega^2',
'\alpha+\beta\omega+\gamma\omega^2', 'Location','best')
title('Rozamiento en el movimiento de rotación')

Referencias

Pascal Klein, Andreas Müller, Sebastian Gröber, Alexander Molz, Jochen Kuhn. Rotational and frictional dynamics of the slamming of a door. Am. J. Phys. 85 (1), January 2017. pp. 30-37