Medida de la velocidad de una bala

Consideramos que el sistema formado por la bala y el bloque es aislado en el momento del choque, por lo que aplicamos el principio de conservación del momento lineal para obtener la velocidad v0 inmediatamente después del choque del sistema formado por el bloque y la bala que se incrustado en él.
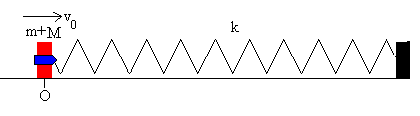
Si M es la masa del bloque, m la masa de la bala y u su velocidad, dicho principio se escribe
mu=(m+M)v0
La energía perdida en el choque es
Estudio energético del sistema después del choque
Supondremos que entre el bloque y el plano horizontal sobre el que desliza hay rozamiento cuyo coeficiente estático es μs y dinámico μk.
La energía cinética del cuerpo de masa (m+M) formado por la bala y el bloque, después del choque se trasforma en trabajo de la fuerza de rozamiento y en energía potencial del muelle deformado.
Las fuerzas que actúan sobre dicho cuerpo son:
-
El peso (m+M)g
-
La reacción del plano N=(m+M)g
-
La fuerza que ejerce el muelle deformado x, k·x
-
La fuerza de rozamiento, de sentido contrario a la velocidad del bloque, fr=μk·N= μk·(m+M)g
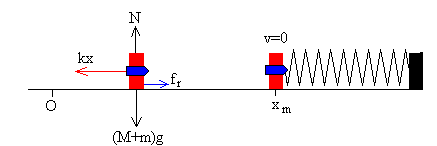
Movimiento del cuerpo hacia la derecha
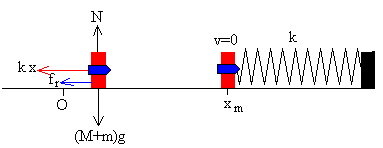
El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía final y la energía inicial del sistema
La máxima deformación del muelle xm se produce cuando v=0.
Midiendo xm despejamos la velocidad u de la bala antes del choque
Si conocemos la velocidad u de la bala antes del choque, resolvemos la ecuación de segundo grado en xm y tomamos la raíz positiva.
Si definimos el parámetro ω2=k/(m+M), Para calcular xm resolvemos la ecuación de segundo grado
El móvil parte de xm con velocidad inicial nula siempre que se cumpla que kxm≥ μs(m+M)g, en caso contrario la posición xm será la posición final del bloque. Supongamos que se cumple la primera condición.
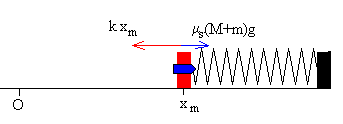
Movimiento del cuerpo hacia la izquierda
El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía final y la energía inicial del sistema
Pueden ocurrir dos casos:
-
Que el cuerpo se pare antes de llegar al origen x=0 si
-
Que llegue al origen con velocidad no nula
Calculamos la posición final xf del cuerpo poniendo v=0.
Calculamos la velocidad vf, del cuerpo cuando pasa por el origen x=0
El bloque deja de estar en contacto con el muelle
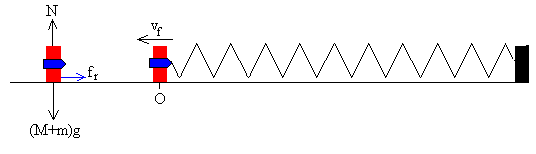
Si el bloque no está sujeto al muelle, el cuerpo formado por el bloque y la bala continúan moviéndose hacia la izquierda hasta que la energía cinética se convierte integramente en trabajo de la fuerza de rozamiento
Ejemplo 1:
-
Coeficiente de rozamiento μs=μk=0.3
-
Masa del bloque, M=1 kg
-
Masa de la bala, m=0.2 kg
-
Velocidad de la bala, u= 10 m/s
-
Constante elástica del muelle, k=20 N/m
Choque de la bala y el bloque
La velocidad del cuerpo formado por la bala y el bloque después del choque es
0.2·10=(0.2+1)·v0, v0=5/3 m/s
El cuerpo se mueve hacia la derecha
La energía cinética inicial de dicho cuerpo, se convierte en trabajo de la fuerza de rozamiento y en energía potencial de deformación del muelle
Despejamos xm en esta ecuación de segundo grado, xm=0.268 m=26.8 cm
En esta posición xm:
-
La fuerza que ejerce el muelle es k·xm=5.37 N
-
La fuerza de rozamiento es μs·(M+m)g=0.3·1.2·9.8=3.53 N
El cuerpo se mueve hacia la izquierda
Comprobamos si la energía potencial elástica es suficiente para llevar el cuerpo al origen
Se para antes de llegar al origen, parte de la energía potencial elástica se convierte en trabajo de la fuerza de rozamiento. Despejamos xf en la ecuación de segundo grado
xf=0.084=8.4 cm
Ejemplo 2:
-
Coeficiente de rozamiento μs=μk=0.1
-
Masa del bloque, M=1 kg
-
Masa de la bala, m=0.2 kg
-
Velocidad de la bala, u= 10 m/s
-
Constante elástica del muelle, k=20 N/m
Choque de la bala y el bloque
La velocidad del cuerpo formado por la bala y el bloque después del choque es
0.2·10=(0.2+1)·v0, v0=5/3 m/s
El cuerpo se mueve hacia la derecha
La energía cinética inicial de dicho cuerpo, se convierte en trabajo de la fuerza de rozamiento, y en energía potencial de deformación del muelle
Despejamos xm en esta ecuación de segundo grado, xm=0.354 m=34.5 cm
En esta posición:
-
La fuerza que ejerce el muelle es k·xm=7.07 N
-
La fuerza de rozamiento es μs·(M+m)g=0.1·1.2·9.8=1.18 N
El cuerpo se mueve hacia la izquierda
Comprobamos si la energía potencial elástica es suficiente para llevar el cuerpo al origen
Llega al origen con velocidad no nula, la energía potencial elástica se convierte en trabajo de la fuerza de rozamiento y en energía cinética de dicho cuerpo.
Despejamos vf =1.18 m/s hacia la izquierda
El bloque deja de estar en contacto con el muelle
El bloque deja de tener contacto con el muelle y el cuerpo se mueve hacia la izquierda del origen hasta que se para. La energía cinética se convierte integramente en trabajo de la fuerza de rozamiento
|x|=0.710 m, x=-7.10 cm
Actividades
Se introduce
-
El coeficiente de rozamiento μs=μk, entre el bloque y el plano sobre el cual desliza, en el control titulado Coef. rozamiento.
-
La masa m de la bala en kg, en el control titulado Masa bala.
-
La velocidad u de la bala antes del choque en m/s, en el control titulado Velocidad bala.
-
La masa del bloque se ha fijado en M=1 kg.
-
La constante k del muelle elástico en N/m, en el control titulado Constante muelle.
Se pulsa el botón titulado Nuevo
Se observa el movimiento de la bala antes del choque, y del cuerpo formado por la bala y el bloque después del choque.
En la parte superior, se proporciona los datos relativos, el tiempo parcial t en segundos, la posición x en cm, la velocidad v de la bala en m/s y la energía del sistema formado por la bala, el bloque y el muelle, en cada instante.
Se dibujan mediante fechas las fuerzas sobre el cuerpo formado por el bloque y la bala después del choque.
Ecuaciones del movimiento
Después del choque, la bala y el bloque forman un cuerpo de masa (M+m) que se mueve hacia la derecha con velocidad inicial v0, bajo la acción de las siguientes fuerzas:
-
El peso (m+M)g
-
La reacción del plano N=(m+M)g
-
La fuerza que ejerce el muelle deformado x, k·x
- La fuerza de rozamiento, de sentido contrario a la velocidad del bloque, fr=μk·N= μk·(m+M)g
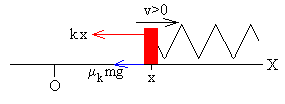
Cuando el bloque se mueve hacia la derecha (v>0), la ecuación del movimiento es
(m+M)a=-kx- μk(m+M)g,
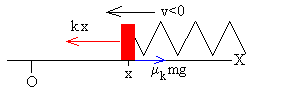
Cuando el bloque se mueve hacia la izquierda (v<0), la fuerza de rozamiento cambia de sentido y la ecuación del movimiento es
(m+M)a=-kx+μk(m+M)g,
Escribimos las ecuaciones del movimiento en forma de ecuación diferencial
con ω2=k/(m+M)
Las ecuaciones del movimiento nos recuerdan la ecuación diferencial de un MAS, pero además tiene un término adicional ±μkg
La solución de la ecuación diferencial es la suma de la homogénea (la ecuación de un MAS) más una constante C. Introduciendo la solución particular (la constante C) en la ecuación diferencial
ω2C=±μkg, C=±μkg/ω2
La solución completa de cada una de las ecuaciones diferenciales es
En ambos casos, la velocidad del conjunto bala-bloque es
Los coeficientes A y B se determinan a partir de las condiciones iniciales
-
El cuerpo se mueve hacia la derecha v>0.
-
El cuerpo se mueve hacia la izquierda v<0
-
El bloque deja de estar en contacto con el muelle
El conjunto bala-bloque inmeditamente después del choque lleva una velocidad v0 y se encuentra en el origen x=0 en el instante t=0.
0=B-μkg/ω2
v0=Aω
La posición x y la velocidad v del cuerpo en su movimiento hacia la derecha es
El máximo desplazamiento xm se produce cuando la velocidad es nula v=0, en el instante t tal que
Teniendo en cuanta las relaciones
Llegamos después de algunas operaciones a la expresión para el máximo desplazamiento xm
El móvil parte de xm con velocidad inicial nula siempre que se cumpla que kxm≥ μs(m+M)g, en caso contrario la posición xm será la posición final del bloque. Supongamos que se cumple la primera condición.
Ponemos el contador de tiempo parcial t a cero, el cuerpo parte de la posición xm con velocidad nula, las constantes A y B de la ecuación de la posición para v<0 valen
xm=B+μkg/ω2
0=Aω
La posición x y la velocidad v de dicho cuerpo en su movimiento hacia la izquierda es
Para que el móvil pase por el origen x=0, se tiene que cumplir que
Para que |cos(ωt)|<1 se tiene que cumplir que ω2xm>2μkg. Esta condición equivale a que la energía potencial del muelle en la posición xm sea mayor que el trabajo de la fuerza de rozamiento
El cuerpo pasa por el origen x=0 en el instante t tal que
La velocidad vf que lleva al pasar por el origen x=0 es
Como el radicando no puede ser negativo se tiene que cumplir que ω2xm≥2μkg
En el caso que ω2xm<2μkg el móvil se para antes de llegar al origen, en el instante t en el que v=0 ó sen(ωt)=0, ωt=π. La posición de parada es
Como vemos xf>0 si ω2xm<2μkg
Cuando el bloque deja de estar en contacto con el muelle la única fuerza que actúa sobre el cuerpo es la de rozamiento. El movimiento es rectilíneo, uniformemente acelerado. De nuevo, ponemos el contador de tiempo parcial a cero.
El cuerpo se para cuando v=0, en la posición
Ejemplo 1:
-
Coeficiente de rozamiento μs=μk=0.3
-
Masa del bloque, M=1 kg
-
Masa de la bala, m=0.2 kg
-
Velocidad de la bala, u= 10 m/s
-
Constante elástica del muelle, k=20 N/m
Choque de la bala y el bloque
La velocidad del cuerpo formado por el bloque y la bala después del choque es
0.2·10=(0.2+1)·v0, v0=5/3 m/s
El cuerpo se mueve hacia la derecha
La frecuencia angular
La posición y velocidad de dicho cuerpo en función del tiempo t son
El máximo desplazamiento xm se produce cuando la velocidad es nula v=0, en el instante t tal que
En esta posición, xm
-
La fuerza que ejerce el muelle es k·xm=5.37 N
-
La fuerza de rozamiento es μs·(M+m)g=0.3·1.2·9.8=3.53 N
El cuerpo se mueve hacia la izquierda
Como ω2xm<2μkg es decir, 4.082·0.268<2·0.3·9.8, el móvil se para antes de llegar al origen, en el instante ωt=π, tf=0.77 s, cuando se encuentra en la posición xf.
Ejemplo 2:
-
Coeficiente de rozamiento μs=μk=0.1
-
Masa del bloque, M=1 kg
-
Masa de la bala, m=0.2 kg
-
Velocidad de la bala, u= 10 m/s
-
Constante elástica del muelle, k=20 N/m
Choque de la bala y el bloque
La velocidad del cuerpo formado por el bloque y la bala del choque es
0.2·10=(0.2+1)·v0, v0=5/3 m/s
El cuerpo se mueve hacia la derecha
La frecuencia angular
La posición y velocidad de dicho cuerpo en función del tiempo t son
El máximo desplazamiento xm se produce cuando la velocidad es nula v=0, en el instante ttal que
En esta posición, xm
-
La fuerza que ejerce el muelle es k·xm=7.07 N
-
La fuerza de rozamiento es μs·(M+m)g=0.1·1.2·9.8=1.18 N
El cuerpo se mueve hacia la izquierda
Como ω2xm>2μkg es decir, 4.082·0.354 >2·0.1·9.8, el móvil cruza el origen, en el instante
La velocidad del cuerpo cuando pasa por el origen es
El muelle deja de actuar sobre el bloque
Las ecuaciones del movimiento rectilíneo uniformemente acelerado del cuerpo son
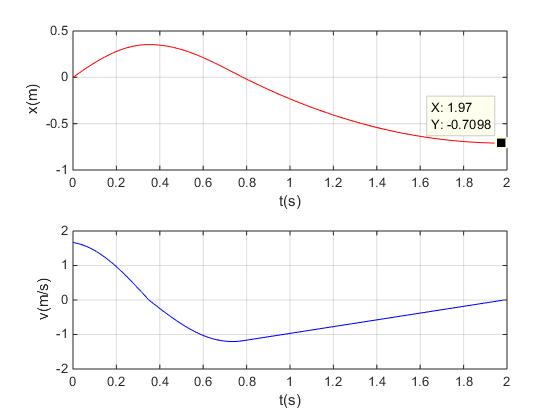
En esta etapa tarda 1.2 s en detenerse. El tiempo total que desde que la bala y el bloque chocan en el origen y se detienen es de 0.350+0.434+1.204=1.988 s, en la posición x=-0.710 m= -7.10 cm
Utilizando MATLAB
Escribimos el script siguiente, para representar la posición x y la velocidad v de la bala y el bloque después del choque.
mu=0.1; %coeficiente cinético de rozamiento
M=1; %masa bloque
m=0.2; %masa bala
u=10; %velocidad inicial de bala
k=20; %constante del muelle
g=9.8; %aceleración de la gravedad
v0=m*u/(m+M); %velocidad de la bala-bloque después del choque
w=sqrt(k/(m+M)); %frecuencia angular
t1=atan(v0*w/(mu*g))/w; %tiempo de la primera etapa
xm=(sqrt(v0^2*w^2+mu^2*g^2)-mu*g)/w^2;
if (w^2*xm)>(2*mu*g) %pasa por el origen
t2=(pi-acos(mu*g/(w^2*xm-mu*g)))/w;
v2=-sqrt(w^2*xm^2-2*mu*g*xm);
t3=-v2/(mu*g);
x3=-v2^2/(2*mu*g);
else %se detine antes de llegar al origen
t2=pi/w;
v2=0;
x2=-xm+2*mu*g/w^2;
t3=0;
end
tf=t1+t2+t3;
t=0:0.01:tf;
x=(v0*sin(w*t)/w+mu*g*(cos(w*t)-1)/w^2).*(t<t1)+
((xm-mu*g/w^2)*cos(w*(t-t1))+mu*g/w^2).*(t1<=t & t<(t1+t2))+
(v2*(t-t1-t2)+mu*g*(t-t1-t2).^2/2).*((t1+t2)<=t);
v=(v0*cos(w*t)-mu*g*sin(w*t)/w).*(t<t1)+
(-(xm*w-mu*g/w)*sin(w*(t-t1))).*(t1<=t & t<(t1+t2))+
(v2+mu*g*(t-t1-t2)).*((t1+t2)<=t);
subplot(2,1,1)
plot(t,x, 'red')
grid on
xlabel('t(s)')
ylabel('x(m)')
subplot(2,1,2)
plot(t,v,'blue')
grid on
xlabel('t(s)')
ylabel('v(m/s)')