El problema se divide en dos etapas, tal como se muestra en la figura:

• Choque entre la bala y el bloque.

Sea v₀ la velocidad inmediatamente después del choque del sistema formado por el péndulo y la bala incrustada en él.

Si M es la masa del bloque, m la masa de la bala y u su velocidad, el principio de conservación del momento lineal, se escribe

mu=(m+M)v₀

• El conjunto bala-bloque se eleva una altura h.

El principio de conservación de la energía después del choque, se escribe

${\displaystyle \begin{array}{l}\frac{1}{2}(m+M)v_0^2=(m+M)gh\\ h=\frac{1}{2g}{\left(\frac{m}{m+M}u\right)}^2\end{array}}$

Si el choque fuera elástico

• Choque elástico entre la bala y el bloque: conservación del momento lineal, la energía cinética de las dos partículas se mantiene constante

${\displaystyle \begin{array}{l}mu=mv+M{v}_0\\ \frac{1}{2}m{u}^2=\frac{1}{2}m{v}^2+\frac{1}{2}M{v}_0^2\end{array}\}{v}_0=2\frac{m}{m+M}u}$

• El bloque se eleva una altura h después del choque

${\displaystyle \begin{array}{l}\frac{1}{2}M{v}_0^2=Mgh\\ h=\frac{1}{2g}{\left(2\frac{m}{m+M}u\right)}^2\end{array}}$

El péndulo se elevaría una altura cuatro veces mayor

En el caso del péndulo balístico la bala penetra en el bloque, el choque es completamente inelástico

Después de la colisión

Después de la colisión pueden ocurrir los siguientes casos, (véase el bucle) dependiendo del valor de la energía cinética adquirida por el sistema formado por el péndulo y la bala incrustada en él.

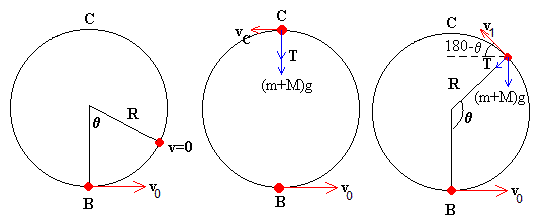
1. Que el ángulo máximo de desviación del péndulo no supere los 90º

La conservación de la energía se escribe

${\displaystyle \frac{1}{2}(m+M)v_0^2=(m+M)gR(1-\cos \theta )}$

Midiendo el ángulo θ obtenemos v₀ y de la conservación del momento lineal obtenemos la velocidad de la bala u.

2. Que el péndulo dé vueltas

${\displaystyle \frac{1}{2}(m+M)v_0^2=\frac{1}{2}(m+M)v_C^2+2(m+M)gR}$

Ahora bien, la velocidad en el punto más alto C debe superar un valor mínimo.

De la dinámica del movimiento circular tenemos que

${\displaystyle \left(m+M\right)g+T=\left(m+M\right)\frac{v_C^2}{R}}$

Siendo T la tensión de la cuerda. La velocidad mínima se obtiene cuando T=0,

$v_{Cmín}=\sqrt{Rg}$ . Entonces $v_0^2=5gR$

3. Que el péndulo se desvíe un ángulo comprendido entre 90º y 180º

De la dinámica del movimiento circular y el principio de conservación de la energía tenemos que

${\displaystyle \begin{array}{l}T+\left(m+M\right)g\cos (180-\theta )=\left(m+M\right)\frac{v^2}{R}\\ \frac{1}{2}(m+M)v_0^2=\frac{1}{2}(m+M)v^2+(m+M)gR\left(1+\cos (180-\theta )\right)\end{array}}$

La cuerda del péndulo deja de tener efecto en el instante en el que su tensión es cero T=0. Por lo que

${\displaystyle v_0^2=gR\left(2-3\cos \theta \right)\theta >90}$

En dicho instante, la partícula se mueve bajo la única fuerza de su propio peso describiendo un movimiento curvilíneo bajo la aceleración constante de la gravedad o un tiro parabólico



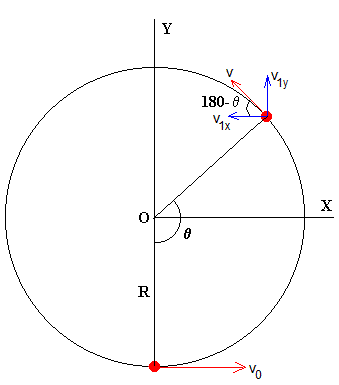
En dicho instante, la partícula se mueve bajo la única fuerza de su propio peso describiendo un movimiento curvilíneo bajo la aceleración constante de la gravedad o un tiro parabólico

${\displaystyle \begin{array}{l}{v}_{1x}=v\cos \left(180-\theta \right)v_{1y}=v\sin \left(180-\theta \right)\\ x=R\sin \left(180-\theta \right)-v_{1x}ty=R\cos \left(180-\theta \right)+v_{1y}t-\frac{1}{2}g{t}^2\end{array}}$

Tomando el centro del bucle como origen de coordenadas. El péndulo vuelve a oscilar cuando se cumpla que $x^2+y^2=R^2$

Un estudio detallado de la interesante combinación de movimiento circular y parabólico se encuentra en la sección, más abajo, "Trayectoria circular y parabólica". Véase también el ejemplo análogo del movimiento de una partícula en un bucle.

Ejemplo1

• Velocidad de la bala, u=10 m/s
• Masa de la bala, m=0.2 kg
• Masa del bloque, M=1.5 kg

• La longitud del péndulo es R=0.5 m

La velocidad v₀ del conjunto formado por la bala y el bloque inmediatamente después del choque, es

m·u=(m+M)v₀,   v₀=1.18 m/s

Aplicamos el principio de conservación de la energía para calcula la máxima desviación del péndulo

${\displaystyle \frac{1}{2}(m+M)v_0^2=(m+M)ghh=R-R\cos \theta }$

Conocido v₀ despejamos h=0.07 m, y calculamos el ángulo θ=30.8º

Ejemplo 2

¿Cuál debe ser la velocidad mínima u de la bala para que el péndulo describa una circunferencia?.

• Masa de la bala, m=0.2 kg
• Masa del bloque, M=1.5 kg
• La longitud del péndulo es R=0.5 m

Calculamos la velocidad mínima v_C de la partícula en el punto más alto de la trayectoria circular, cuando la tensión de la cuerda es cero, aplicando la ecuación de la dinámica del movimiento circular uniforme.

${\displaystyle v_C=\sqrt{9.8·0.5}=2.21\text{m/s}}$

Aplicando el principio de conservación de la energía, calculamos la velocidad de la partícula en el punto B más bajo de la trayectoria circular.

${\displaystyle \frac{1}{2}(m+M)v_0^2=\frac{1}{2}(m+M)v_C^2+(m+M)g·2R{v}_0=4.95\text{m/s}}$

Aplicamos el principio de conservación del momento lineal, para calcular la velocidad de la bala u antes del choque

m·u=(M+m)v₀,   u=42.07 m/s

Ejemplo 3

• Velocidad de la bala, u=35 m/s
• Masa de la bala, m=0.2 kg
• Masa del bloque, M=1.5 kg

• La longitud del péndulo es R=0.5 m

La velocidad v₀ del conjunto formado por la bala y el bloque inmediatamente después del choque, es

m·u=(m+M)v₀,   v₀=4.12 m/s

Aplicamos el principio de conservación de la energía, para calcular la máxima desviación del péndulo

${\displaystyle \frac{1}{2}(m+M)v_0^2=(m+M)ghh=R-R\cos \theta }$

Conocido v₀ despejamos h=0.87 m, que es mayor que la longitud R=0.5 del péndulo

La cuerda del péndulo deja de tener efecto en el instante en el que su tensión es cero T=0. Por lo que

${\displaystyle \begin{array}{l}\left(m+M\right)g\cos (180-\theta )=\left(m+M\right)\frac{v^2}{R}\\ \frac{1}{2}\left(m+M\right)v_0^2=\frac{1}{2}\left(m+M\right)v^2+\left(m+M\right)gR\left(1+\cos (180-\theta )\right)\end{array}}$

En este sistema de ecuaciones, calculamos el ángulo θ=119.1º y la velocidad de la partícula v=1.54 m/s

El movimiento posterior de la partícula viene descrito por las siguientes ecuaciones del tiro parabólico.

${\displaystyle \begin{array}{l}{v}_{1x}=v\cos (180-\theta )=0.75\text{m/s}{v}_{1y}=v\sin (180-\theta )=1.35\text{m/s}\\ x=0.44-0.75·ty=0.24+1.35·t-4.9·t^2\end{array}}$

Ejemplo 4

• Masa de la bala, m=0.2 kg
• Masa del bloque, M=1.5 kg

• La longitud del péndulo es R=0.5 m

Calculamos la velocidad u de la bala para que el conjunto bala-bloque después del choque pase por el punto de suspensión del péndulo

Como deduciremos en el apartado titulado 'Trayectoria circular y parabólica', la velocidad del conjunto bala-bloque después del choque deberá ser

${\displaystyle v_0^2=gR\left(2+\sqrt{3}\right)}$

v₀=4.28 m/s. Aplicando el principio de conservación del momento lineal

m·u=(m+M)v₀,   u=36.35 m/s

Actividades

Se introduce

• La masa de la bala en kg, en el control titulado Masa bala
• La velocidad de la bala en m/s, en el control titulado Velocidad bala
• La masa del bloque que pende de la cuerda en kg, en el control titulado Masa bloque.
• Dato: la longitud del péndulo es de 0.5 m

Se pulsa el botón titulado Nuevo.

Se observa el movimiento del péndulo. Se representa la energía del sistema después del choque.

Se modifica la masa del bloque de modo que se pueda medir la desviación del péndulo en la escala graduada.

Trayectoria circular y parabólica

1. La partícula describe una trayectoria circular si la velocidad en la parte más baja del bucle es

${\displaystyle v_0\ge \sqrt{5Rg}}$

2. La partícula se mueve hacia atrás cuando

${\displaystyle v_0\le \sqrt{2Rg}}$

3. Cuando la velocidad v₀ está comprendida entre estos dos valores, la partícula describe una trayectoria circular y a continuación, una trayectoria parabólica.

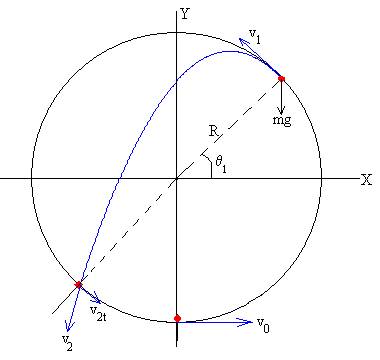
Para analizar este movimiento, situamos el origen en el centro de la trayectoria circular y medimos los ángulos desde el eje X. El nivel cero de energía potencial lo situamos en el eje X. La energía de la partícula es

${\displaystyle E_1=\frac{1}{2}m{v}_0^2-mgR}$

En la posición angular θ₁ la partícula abandona la trayectoria circular, la tensión T de la cuerda es nula. La ecuación de la dinámica del movimiento circular se escribe

${\displaystyle mg\sin {\theta }_1=m\frac{v_1^2}{R}}$

Conocida la energía de la partícula E₁, determinamos el valor del ángulo θ₁

${\displaystyle E_1=\frac{1}{2}m{v}_1^2+mgR\sin {\theta }_1=\frac{3}{2}mgR\sin {\theta }_1}$

Para que la partícula describa una trayectoria parbólica, se tiene que cumplir que 0<E₁<3mgR/2

Una vez que llega P₁, describe una trayectoria parabólica, la velocidad y la posición de la partícula son

${\displaystyle \{\begin{array}{l}{v}_x=-v_1\sin {\theta }_1\\ v_y=v_1\cos {\theta }_1-gt\end{array}\{\begin{array}{l}x=R\cos {\theta }_1-v_1\sin {\theta }_{1}t\\ y=R\sin {\theta }_1+v_1\cos {\theta }_{1}t-\frac{1}{2}g{t}^2\end{array}}$

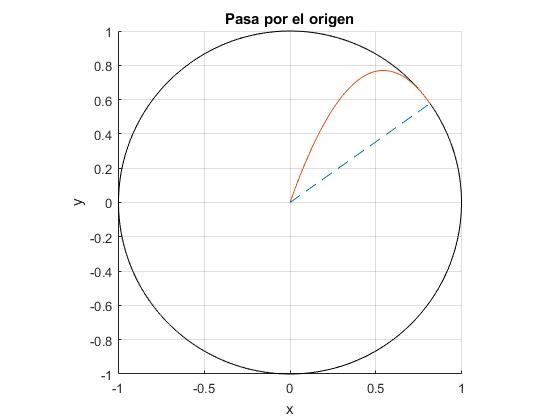
El caso particular más interesante es aquél en el que la partícula pasa por el origen, x=0, y=0. En la ecuación de la trayectoria, despejamos, v₁

${\displaystyle v_1^2=\frac{Rg}{2}\frac{{\cos }^2{\theta }_1}{\sin {\theta }_1}}$

En la ecuación de la dinámica del movimiento circular, calculamos θ₁

${\displaystyle \tan {\theta }_1=\frac{1}{\sqrt{2}}}$

Conocido el ángulo θ₁=35.3°, aplicamos el principio de conservación de la energía para calcular la velocidad v₀ de la partícula en el punto más bajo de la trayectoria circular

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2-mgR=\frac{3}{2}mgR\sin {\theta }_1\\ v_0^2=gR\left(2+\sqrt{3}\right)\end{array}}$

R=1; %radio
hold on
fplot(@(t) cos(t),@(t) sin(t),[0,2*pi],'color','k')
th=atan(1/sqrt(2));
v=sqrt(R*sin(th)*9.8); %velocidad disparo
T=sqrt(2)*R/v; %tiempo de vuelo
fplot(@(t) (R*cos(th)-v*sin(th)*t), @(t) R*sin(th)+v*cos(th)*t-4.9*t.^2,[0,T])
line([0,R*cos(th)],[0,R*sin(th)],'lineStyle','--')
hold off
grid on
axis square
xlabel('x')
ylabel('y')
title('Pasa por el origen')

Impacto

En el punto P₂ la distancia entre la partícula y el centro vuelve a ser R. P₂ es el punto de intersección entre la parábola y la circunferencia de radio R. Recordando que la ecuación de una circunferencia, cuando su centro está en el origen de coordenadas es

${\displaystyle \begin{array}{l}{x}^2+y^2=R^2\\ {\left(R\cos {\theta }_1-v_1\sin {\theta }_{1}t\right)}^2+{\left(R\sin {\theta }_1+v_1\cos {\theta }_{1}t-\frac{1}{2}g{t}^2\right)}^2=R^2\end{array}}$

Teniendo en cuenta que de la dinámica del movimiento circular

${\displaystyle v_1^2=Rg\sin {\theta }_1}$

Llegamos a la siguiente expresión simplificada

${\displaystyle t^{3}g\left(\frac{1}{4}gt-v_1\cos {\theta }_1\right)=0}$

El tiempo de vuelo de la partícula hasta que llega a P₂ es

${\displaystyle t=\frac{4v_1\cos {\theta }_1}{g}}$

La posición del punto P₂ y la velocidad de la partícula son, respectivamente

${\displaystyle \{\begin{array}{l}{v}_{2x}=-v_1\sin {\theta }_1\\ v_{2y}=-3v_1\cos {\theta }_1\end{array}\{\begin{array}{l}{x}_2=R\cos {\theta }_1-\frac{4v_1^2\sin {\theta }_1\cos {\theta }_1}{g}=-3R\cos {\theta }_1+4R{\cos }^3{\theta }_1\\ y_2=R\sin {\theta }_1-\frac{4v_1^2{\cos }^2{\theta }_1}{g}=R\sin {\theta }_1-4R\sin {\theta }_1{\cos }^2{\theta }_1\end{array}}$

Supondremos que cuando la cuerda se estira al máximo, se anula la componente normal de la velocidad y la partícula describe de nuevo una trayectoria circular con la componente tangencial de dicha velocidad como velocidad inicial.

La componente normal de la velocidad se calcula mediante el producto escalar $\overrightarrow{r_2}·\overrightarrow{v_2}$

${\displaystyle v_{2r}=\frac{\overrightarrow{r_2}·\overrightarrow{v_2}}{R}{v}_{2t}^2=v_2^2-v_{2r}^2}$

El módulo del vector posición $\overrightarrow{r_2}$ del punto P₂ es el radio R de la circunferencia

${\displaystyle \begin{array}{l}{v}_{2r}=8v_1\sin {\theta }_1{\cos }^3{\theta }_1\\ v_{2t}^2=v_1^2(1+8{\cos }^2{\theta }_1-64{\cos }^6{\theta }_1+64{\cos }^8{\theta }_1)\\ v_{2t}=v_1(1+4{\cos }^2{\theta }_1-8{\cos }^4{\theta }_1)\end{array}}$

Si v_2t es positiva la partícula se mueve hacia la derecha (como se ve en la figura más arriba), si es negativa, se mueve hacia la izquierda

La energía de la partícula en el punto P₂ final de la trayectoria parabólica es

${\displaystyle E_2=\frac{1}{2}m{v}_{2t}^2+mg{y}_2=mgR\sin {\theta }_1\left(\frac{3}{2}-32{\cos }^6{\theta }_1{\sin }^2{\theta }_1\right)}$

Esta energía E₂ es menor que la energía de la partícula en el punto de partida, E₁

Si la energía E₂ de la partícula es positiva, calculamos el nuevo ángulo θ₂, dibujamos la trayectoria parabólica y así, sucesivamente. Las líneas a trazos marcan el inicio y fin de cada una de las trayectorias parabólicas

k=1.36; %E/(mgR), proporción de energía, k>0, k<3/2
R=1;
hold on
fplot(@(t) cos(t),@(t) sin(t),[0,2*pi],'color','k')
signo=1;
disp([k,1])
for i=1:5 %hasta cinco trayectorias
    th=asin(2*k/3); %ángulo
    v=sqrt(R*sin(th)*9.8); %velocidad disparo
    T=4*v*cos(th)/9.8; %tiempo de vuelo
    fplot(@(t) signo*(R*cos(th)-v*sin(th)*t), @(t) R*sin(th)+
v*cos(th)*t-4.9*t.^2,[0,T])
    line([0,signo*R*cos(th)],[0,R*sin(th)],'lineStyle','--')
    line([0,signo*(-3*R*cos(th)+4*R*cos(th)^3)],[0,R*sin(th)-
4*R*sin(th)*cos(th)^2],'lineStyle','--')
    k=sin(th)*(3/2-32*cos(th)^6*sin(th)^2);
    v_2t=v*(1+4*cos(th)^2-8*cos(th)^4);
    signo=1;
    if v_2t<0
        signo=-1;
    end
     %disp([k,v_2t])
    if k<0
        break;
    end
    disp([k,sign(v_2t)])
end
hold off
axis square
axis off

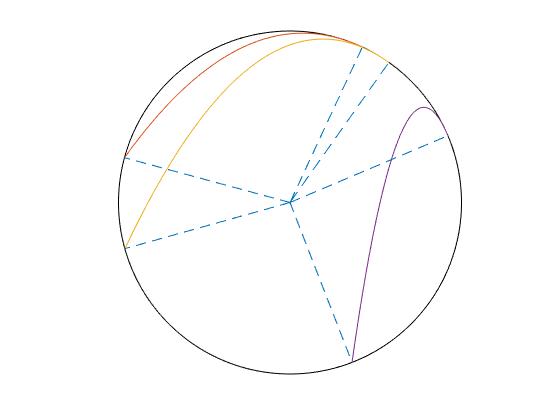
El programa imprime el valor de la energía en unidades mgR y el signo de la componente tangencial de la velocidad en la posición final P₂

    1.3600    1.0000
    1.2256    1.0000
    0.5845    1.0000

En la figura, vemos que para el valor de la energía k=1.36 se obtienen tres trayectorias parabólicas. Se sugiere al lector probar con k=1.40, 1.41, 1.42, etc. El script puede dibujar hasta cinco trayectorias

Referencias

Alain Goriely, Philippe Boulanger and Jules Leroy. Toy models: the jumping pendulum. Am. J. Phys. 74 (9) September 2006, pp. 784-788