Choques en dos dimensiones

El objetivo de esta página es el de estudiar los choques bidimensionales de dos partículas en el Sistema de Referencia del Laboratorio (Sistema-L) y en el Sistema de Referencia del Centro de Masas (Sistema–C).

Sistema de Referencia del Laboratorio

Supongamos que chocan dos discos o esferas de masas m₁ y m₂ y radios r₁ y r₂.

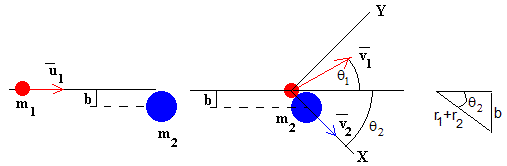
Se denomina parámetro de impacto b a la distancia entre la dirección de la velocidad del primer disco $\vec{u_{1}}$ y el centro del segundo disco que suponemos inicialmente en reposo.

b=(r₁+r₂)·sinθ₂

Las velocidades de los discos antes del choque respecto del sistema de ejes X e Y

$\begin{array}{l} \vec{u_{1}} = u_{1} \cos θ_{2} \hat{i} + u_{1} \sin θ_{2} \hat{j} \\ \vec{u_{2}} = 0 \end{array}$

Las velocidades de discos después del choque respecto del sistema de ejes X e Y

$\begin{array}{l} \vec{v_{1}} = v_{1} \cos (θ_{1} + θ_{2}) \hat{i} + v_{1} \sin (θ_{1} + θ_{2}) \hat{j} \\ \vec{v_{2}} = v_{2} \hat{i} \end{array}$

El principio de conservación del momento lineal se escribe

$m_{1} \vec{u_{1}} + m_{2} \vec{u_{2}} = m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}}$

o bien,

$\begin{array}{l} m_{1} u_{1} \cos θ_{2} = m_{2} v_{2} + m_{1} v_{1} \cos (θ_{2} + θ_{1}) \\ m_{1} u_{1} \sin θ_{2} = m_{1} v_{1} \sin (θ_{2} + θ_{1}) \end{array}$

El coeficiente de restitución nos mide el cociente cambiado de signo, entre la velocidad relativa de alejamiento a lo largo del eje X y la velocidad relativa de aproximación a lo largo del mismo eje.

$e = \frac{v_{2} - v_{1} \cos (θ_{2} + θ_{1})}{u_{1} \cos θ_{2}}$

Dado el parámetro de impacto b obtenemos el ángulo θ₂. De la segunda y tercera ecuación, despejamos el ángulo entre las direcciones de las velocidades de los discos después del choque

$\begin{array}{l} \tan (θ_{2} + θ_{1}) = \frac{m_{1} + m_{2}}{m_{1} - e m_{2}} \tan θ_{2} \\ v_{1} = \frac{u_{1} \sin θ_{2}}{\sin (θ_{2} + θ_{1})} v_{2} = \frac{m_{1} u_{1} (1 + e) \cos θ_{2}}{m_{1} + m_{2}} \end{array}$

Choques elásticos

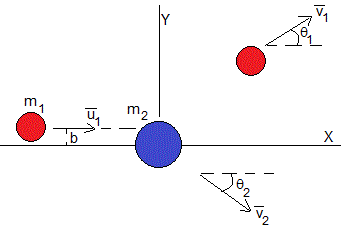
En este apartado estudiamos los choques de dos discos de radios r₁ y r₂ y de masas m₁ y m₂. El disco de masa m₂ está en el origen en reposo. El disco de masa m₁ se mueve paralelamente al eje X a una distancia b (parámetro de impacto) con velocidad u₁

Vamos a calcular las velocidades de los discos después del choque v₁ y v₂ y las direcciones de dichas velocidades, θ₁ y θ₂, que son los ángulos que forma el vector velocidad con el eje X

Principio de conservación del momento lineal

$m_{1} \vec{u_{1}} = m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} {\begin{cases} m_{1} u_{1} = m_{1} v_{1} \cos θ_{1} + m_{2} v_{2} \cos θ_{2} \\ m_{1} v_{1} \sin θ_{1} = m_{2} v_{2} \sin θ_{2} \end{cases}$

Conservación de la energía

$\frac{1}{2} m_{1} u_{1}^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2}$

Tenemos un sistema de tres ecuaciones con cuatro incógnitas, una de las cuales el ángulo θ₂ se obtiene a partir del parámetro de impacto b y de los radios de los dos discos r₁ y r₂ tal como se aprecia en la primera figura.

$\sin θ_{2} = \frac{b}{r_{1} + r_{2}}$

Llamando D=r₁+r₂, sinθ₂=b/D

Despejamos v₁ en la segunda ecuación y la sustituimos en la primera

$\begin{array}{l} v_{1} = \frac{m_{2} v_{2} \sin θ_{2}}{m_{1} \sin θ_{1}} \\ u_{1} = \frac{m_{2} v_{2} \sin (θ_{1} + θ_{2})}{m_{1} \sin θ_{1}} \end{array}$

Introducimos estas expresiones en la ecuación de la conservación de la energía. Para ello, utilizamos la relación trigonométrica, sin²A-sin²B=sin(A+B)sin(A-B), obteniendo una relación entre los ángulos θ₁ y θ₂

$\sin (θ_{1} + 2 θ_{2}) = \frac{m_{1}}{m_{2}} \sin θ_{1}$

Utilizando la relación trigonométrica sin(A+B)=sinA·cosB+sinB·cosA

$\begin{array}{l} \tan θ_{1} = \frac{\sin (2 θ_{2})}{\frac{m_{1}}{m_{2}} - \cos (2 θ_{2})} \\ \tan θ_{1} = \frac{2 \sin θ_{2} \sqrt{1 - \sin^{2} θ_{2}}}{\frac{m_{1}}{m_{2}} - 1 + 2 \sin^{2} θ_{2}} \end{array}$

Si el denominador es positivo, el ángulo θ₁<90°, si el denominador es negativo el ángulo es el suplementario.

Casos particulares

Llamaremos m≥1 al cociente m=m₂/m₁. Las cuatro ecuaciones que nos proporcionan las velocidades finales de los discos después del choque v₁ y v₂ y sus direcciones, θ₁ y θ₂, son

$\begin{array}{l} \sin θ_{2} = \frac{b}{D} \\ \sin (θ_{1} + 2 θ_{2}) = \frac{1}{m} \sin θ_{1} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} \\ u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \end{array}$

m₁=m₂, m=1

Direcciones, θ₁ y θ₂

$\begin{array}{l} \sin (θ_{1} + 2 θ_{2}) = \frac{1}{m} \sin θ_{1} \\ \sin (θ_{1} + 2 θ_{2}) = \sin θ_{1} \\ θ_{1} + 2 θ_{2} = 180 - θ_{1} \\ θ_{1} + θ_{2} = 90 \end{array}$

Conocido θ₂, sinθ₂=b/D, calculamos θ₁. Las direcciones de la velocidades finales son perpendiculares.

Velocidades, v₁ y v₂

$\begin{array}{l} u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \\ v_{2} = u_{1} \sin θ_{1} = u_{1} \cos θ_{2} = u_{1} \sqrt{1 - \frac{b^{2}}{D^{2}}} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} \\ v_{1} = u_{1} \cos θ_{2} \frac{\sin θ_{2}}{\cos θ_{2}} = u_{1} \frac{b}{D} \end{array}$

Ejemplo

Sean dos discos de radio unidad, D=2. El disco de masa m₁ lleva una velocidad de u₁=3.5 m/s, el parámetro de impacto es b=0.8

>> b=0.8;
>> th_2=asind(b/2)
th_2 =   23.5782
>> th_1=90-th_2
th_1 =   66.4218

>> u1=3.5;
>> v1=u1*b/2
v1 =    1.4000
>> v2=u1*sqrt(1-(b/2)^2)
v2 =    3.2078

Introducimos estos datos en el programa interactivo al final de la página, obtenemos los mismos resultados

θ₁=90°

Parámetro de impacto b, dirección θ₂

$\begin{array}{l} \sin (θ_{1} + 2 θ_{2}) = \frac{1}{m} \sin θ_{1} \\ \cos (2 θ_{2}) = \frac{1}{m} \end{array}$

Como sinθ₂=b/D

$\begin{array}{l} \cos^{2} θ_{2} - \sin^{2} θ_{2} = \frac{1}{m} \\ (1 - \frac{b^{2}}{D^{2}}) - \frac{b^{2}}{D^{2}} = \frac{1}{m} \\ \frac{b}{D} = \sqrt{\frac{1}{2} (1 - \frac{1}{m})} \end{array}$

Velocidades v₁ y v₂

$\begin{array}{l} u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \\ u_{1} = m v_{2} \cos θ_{2} \\ v_{2} = \frac{1}{m \sqrt{1 - \frac{b^{2}}{D^{2}}}} u_{1} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} \\ v_{1} = \frac{\frac{b}{D}}{\sqrt{1 - \frac{b^{2}}{D^{2}}}} u_{1} \end{array}$

Ejemplo

Cuando el cociente de masas m=2, b/D=1/2, θ₂=30°, $v_{1} = v_{2} = \frac{u_{1}}{\sqrt{3}}$ , que podemos comprobar en el programa interactivo al final de la página

θ₂=45°

Parámetro de impacto b, dirección θ₁

El parámetro de impacto, sinθ₂=b/D, $b = \frac{D}{\sqrt{2}}$

Utilizando la relación

$\begin{array}{l} \tan θ_{1} = \frac{\sin (2 θ_{2})}{\frac{1}{m} - \cos (2 θ_{2})} \\ \tan θ_{1} = m \end{array}$

Velocidades v₁ y v₂

$\begin{array}{l} u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \\ u_{1} = m v_{2} (\cos 45 + \frac{1}{\tan θ_{1}} \sin 45) \\ v_{2} = \sqrt{2} \frac{1}{1 + m} u_{1} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} \\ v_{1} = \frac{\sqrt{1 + m^{2}}}{1 + m} u_{1} \end{array}$

Se ha utilizado la relación trigonométrica

$\sin θ_{1} = \frac{\tan θ_{1}}{\sqrt{1 + \tan^{2} θ_{1}}}$

Ejemplo

>> b=2/sqrt(2)
b =    1.4142
>> m=3; 
>> th_1=atand(m)
th_1 =   71.5651

>> u1=3.5;
>> v2=sqrt(2)*u1/(1+m)
v2 =    1.2374
>> v1=u1*sqrt(1+m^2)/(1+m)
v1 =    2.7670

θ₂=θ₁

Parámetro de impacto b, dirección θ₁

$\begin{array}{l} \sin (θ_{1} + 2 θ_{2}) = \frac{1}{m} \sin θ_{1} \\ 3 \sin θ_{2} - 4 \sin^{3} θ_{2} = \frac{1}{m} \sin θ_{2} \\ \sin θ_{2} = \frac{1}{2} \sqrt{3 - \frac{1}{m}} \\ \frac{b}{D} = \frac{1}{2} \sqrt{3 - \frac{1}{m}} \end{array}$

Velocidades v₁ y v₂

$\begin{array}{l} u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \\ u_{1} = 2 m v_{2} \cos θ_{2} = 2 m v_{2} \frac{1}{2} \sqrt{1 + \frac{1}{m}} = v_{2} \sqrt{m (1 + m)} \\ v_{2} = \frac{1}{\sqrt{m (1 + m)}} u_{1} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} = \sqrt{\frac{m}{1 + m}} u_{1} \end{array}$

Ejemplo

>> m=3; 
>> b=sqrt(3-1/3)
b =    1.6330
>> th_2=asind(sqrt(3-1/3)/2)
th_2 =   54.7356

>> u1=3.5;
>> v2=u1/sqrt(m*(1+m))
v2 =    1.0104
>> v1=u1*sqrt(m/(1+m))
v1 =    3.0311

θ₂=θ₁/2

Parámetro de impacto b, dirección θ₁

$\begin{array}{l} \sin (θ_{1} + 2 θ_{2}) = \frac{1}{m} \sin θ_{1} \\ \sin (2 θ_{1}) = \frac{1}{m} \sin θ_{1} \\ \cos θ_{1} = \frac{1}{2 m} \\ \cos (2 θ_{2}) = \frac{1}{2 m} \\ 1 - 2 \sin^{2} θ_{2} = \frac{1}{2 m} \\ 1 - 2 \frac{b^{2}}{D^{2}} = \frac{1}{2 m} \\ \frac{b}{D} = \frac{1}{2} \sqrt{2 - \frac{1}{m}} \end{array}$

Velocidades v₁ y v₂

$\begin{array}{l} u_{1} = \frac{m v_{2} \sin (θ_{1} + θ_{2})}{\sin θ_{1}} \\ u_{1} = m (\cos θ_{2} + \sin θ_{2} \frac{\cos θ_{1}}{\sin θ_{1}}) v_{2} \\ \sin θ_{2} = \frac{1}{2} \sqrt{2 - \frac{1}{m}}, \cos θ_{2} = \frac{1}{2} \sqrt{2 + \frac{1}{m}}, \sin θ_{1} = \frac{1}{2} \sqrt{2 - \frac{1}{m}} \sqrt{2 + \frac{1}{m}} \\ v_{2} = \sqrt{2 + \frac{1}{m}} \frac{1}{1 + m} u_{1} \\ v_{1} = \frac{m v_{2} \sin θ_{2}}{\sin θ_{1}} = \frac{m}{1 + m} u_{1} \end{array}$

Ejemplo

>> m=3; 
>> b=sqrt(2-1/3)
b =    1.2910
>> th_2=asind(sqrt(2-1/m)/2)
th_2 =   40.2030
>> th_1=2*th_2
th_1 =   80.4059
>> v2=sqrt(2+1/m)*u1/(1+m)
v2 =    1.3366
>> v1=m*u1/(1+m)
v1 =    2.6250

Descripción en el Sistema de Referencia del Centro de Masas

La velocidad del centro de masas es el cociente entre el momento lineal total $\vec{P}$ y la masa del sistema de partículas

${\vec{v}}_{c m} = \frac{\vec{P}}{m_{1} + m_{2}} = \frac{m_{1} u_{1} \cos θ_{2}}{m_{1} + m_{2}} \hat{i} + \frac{m_{1} u_{1} \sin θ_{2}}{m_{1} + m_{2}} \hat{j}$

Las velocidades iniciales de las partículas en el Sistema-C son

$\begin{array}{l} \vec{u_{1 c}} = \vec{u_{1}} - \vec{v_{c}} = \frac{m_{2} u_{1}}{m_{1} + m_{2}} (\cos θ_{2} \hat{i} + \sin θ_{2} \hat{j}) \\ \vec{u_{2 c}} = \vec{u_{2}} - \vec{v_{c}} = - \frac{m_{1} u_{1}}{m_{1} + m_{2}} (\cos θ_{2} \hat{i} + \sin θ_{2} \hat{j}) \end{array}$

Las velocidades finales del las partículas en el Sistema-L son

$\begin{array}{l} \vec{v_{1}} = \frac{m_{1} - e m_{2}}{m_{1} + m_{2}} u_{1} \cos θ_{2} \hat{i} + u_{1} \sin θ_{2} \hat{j} \\ \vec{v_{2}} = \frac{m_{1} u_{1} (1 + e) \cos θ_{2}}{m_{1} + m_{2}} \hat{i} \end{array}$

Las velocidades finales del las partículas en el Sistema-C son

$\begin{array}{l} \vec{v_{1 c}} = \vec{v_{1}} - \vec{v_{c}} = \frac{m_{2} u_{1}}{m_{1} + m_{2}} (- e \cdot \cos θ_{2} \hat{i} + \sin θ_{2} \hat{j}) \\ \vec{v_{2 c}} = \vec{v_{_{2}}} - \vec{v_{c}} = \frac{m_{1} u_{1}}{m_{1} + m_{2}} (e \cos θ_{2} \hat{i} - \sin θ_{2} \hat{j}) \end{array}$

Comprobamos que se cumple el principio de conservación del momento lineal en el Sistema-C

$\begin{array}{l} m_{1} \vec{v_{1 c}} + m_{2} \vec{v_{2 c}} = 0 \\ m_{1} \vec{u_{1 c}} + m_{2} \vec{u_{2 c}} = 0 \end{array}$

La energía perdida en la colisión Q es la diferencia de las energías cinéticas después del choque y antes del choque bien referidas al Sistema-L o al Sistema-C. Pero es mucho más fácil calcular esta diferencia en el Sistema-C.

$Q = \frac{1}{2} m_{1} v_{1 c}^{2} + \frac{1}{2} m_{2} v_{2 c}^{2} - \frac{1}{2} m_{1} u_{1 c}^{2} - \frac{1}{2} m_{2} u_{2 c}^{2} = \frac{1}{2} (e^{2} - 1) \frac{m_{1} m_{2}}{m_{1} + m_{2}} u_{1}^{2} \cos^{2} θ_{2}$

Ejemplos

1.-Una partícula de masa 0.2 kg moviéndose a 0.4 m/s choca contra otra partícula de masa 0.3 kg que está en reposo. Después del choque la primera partícula se mueve con 0.2 m/s en una dirección que hace un ángulo de 40º con la dirección inicial.

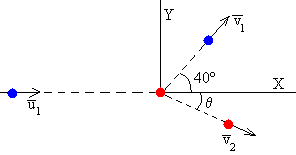
Los datos son

$\begin{array}{l} \vec{u_{1}} = 0.4 \cdot \hat{i} \\ \vec{u_{2}} = 0 \\ \vec{v_{1}} = 0.2 \cos 40 \cdot \hat{i} + 0.2 \sin 40 \cdot \hat{j} \end{array}$

Aplicamos el principio de conservación del momento lineal

$0.2 \cdot \vec{u_{1}} = 0.2 \cdot {\vec{v}}_{1} + 0.3 \cdot {\vec{v}}_{2}$

y despejamos la velocidad $\vec{v_{2}}$ de la segunda partícula después del choque

$\vec{v_{2}} = 0.1645 \cdot \hat{i} - 0.0857 \cdot \hat{j}$

El módulo de la velocidad es v₂=0.1855 m/s, el ángulo que forma con el eje X es θ=-27.5º

La energía que se pierde en la colisión es

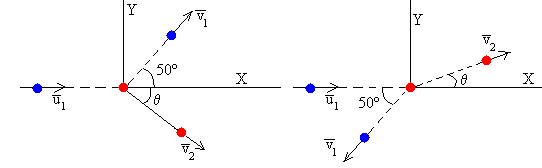
$Q = \frac{1}{2} 0.3 v_{2}^{2} + \frac{1}{2} 0.2 v_{1}^{2} - \frac{1}{2} 0.2 u_{1}^{2} = - 0.0068 J$

2.-Una partícula de 5 kg de masa, moviéndose a 2 m/s choca contra otra partícula de 8 kg inicialmente en reposo. Si el choque es elástico y la primera partícula se ha desviado 50º de la dirección original del movimiento, calcular la velocidad de cada partícula después del choque

Los datos son

$\begin{array}{l} {\vec{u}}_{1} = 2 \cdot \hat{i} \\ {\vec{u}}_{2} = 0 \\ {\vec{v}}_{1} = v_{1} \cos 50 \cdot \hat{i} + v_{1} \sin 50 \cdot \hat{j} \end{array}$

Aplicamos el principio de conservación del momento lineal y despajemos la velocidad $\vec{v_{2}}$ de la segunda partícula después del choque

$5 \cdot \vec{u_{1}} = 5 \cdot \vec{v_{1}} + 8 \cdot \vec{v_{2}}$

Si el choque es elástico la energía cinética de las partículas no cambia

$\frac{1}{2} 5 u_{1}^{2} = \frac{1}{2} 5 v_{1}^{2} + \frac{1}{2} 8 v_{2}^{2}$

En la ecuación de la conservación del momento lineal, despejamos $\vec{v_{2}}$ y calculamos el cuadrado de su módulo

$\vec{v_{2}} = \frac{(10 - 5 v_{1} \cos 50)}{8} \hat{i} + \frac{- 5 v_{1} \sin 50}{8} \hat{j}$

Nos queda la ecuación de segundo grado

$65 v_{1}^{2} - 100 v_{1} \cos 50 - 60 = 0$

La primera solución es

v₁=1.57 m/s

La velocidad de la segunda partícula es

$\vec{v_{2}} = 0.62 \cdot \hat{i} - 0.75 \cdot \hat{j}$

El módulo de v₂=0.97 m/s y hace un ángulo de -50.7º con el eje X, tal como se ve en la parte izquierda de la figura.

La segunda solución es

v₁=-0.59 m/s

La primera partícula se mueve con velocidad v₁=0.59 m/s haciendo un ángulo de 180+50=230º con el eje X.

La velocidad de la segunda partícula es

$\vec{v_{2}} = 1.49 \cdot \hat{i} - 0.28 \cdot \hat{j}$

El módulo de v₂=1.51 m/s y hace un ángulo de 10.7º con el eje X, tal como se ve en la parte derecha de la figura.

3.- Datos del choque

u₁=3.5 m/s
u₂=0
Las partículas tienen la misma masa m₁=m₂=1
El parámetro de impacto b=0.8
El choque elástico e=1

El ángulo θ₂ que forma la dirección de la velocidad de la segunda partícula después del choque es

b=(r₁+r₂)·sinθ₂

0.8=2·sinθ₂, θ₂=23.6º

Calculamos el ángulo θ₁ que forma la dirección de la velocidad de la primera partícula

$\tan (θ_{2} + θ_{1}) = \frac{m_{1} + m_{2}}{m_{1} - e m_{2}} \tan θ_{2} θ_{2} + θ_{1} = 90 º θ_{1} = 66 .4º$

Calculamos la velocidad de la primera partícula después del choque

$v_{1} = \frac{u_{1} \sin θ_{2}}{\sin (θ_{2} + θ_{1})} v_{1} = 1.4 m/s$

Calculamos la velocidad de la segunda partícula después del choque

$v_{2} = \frac{m_{1} u_{1} (1 + e) \cos θ_{2}}{m_{1} + m_{2}} v_{2} = 3.2 m/s$

4.-Datos del choque

u₁=3.5 m/s
u₂=0
m₁=1
m₂=2
El parámetro de impacto b=0.8
Coeficiente de restitución e=0.9

Resultados

0.8=2·sinθ₂, θ₂=23.6º

θ₁=97.8º

v₁=1.64 m/s, v₂=2.03 m/s

Calculamos la energía perdida en la colisión

$Q = \frac{1}{2} 2 v_{2}^{2} + \frac{1}{2} 1 v_{1}^{2} - \frac{1}{2} 1 u_{1}^{2} = - 0.65 J$

O bien, por la fórmula

$Q = \frac{1}{2} (e^{2} - 1) \frac{m_{1} m_{2}}{m_{1} + m_{2}} u_{1}^{2} \cos^{2} θ_{2} Q = - 0.65 J$

Solución con MATLAB

Definimos una función a la que se le pasa la velocidad inicial u₁ de la primera partícula (la segunda estáen reposo, u₂=0), el coeficiente e de restitución, el parámetro de impacto, b, el cociente m₂/m₁ entre las masas de las dos partículas. La función devuelve la velocidad v₁ y v₂ y dirección θ₁ y θ₂ de cada una de las partículas tras el choque

Cuando el parámetro de impacto, b=0, tenemos un choque frontal, que se ha descrito en la página anterior.

function [v1,fi1,v2,fi2] = choque_2(u1,e,b,masa)
%choques frontales
    if b<1e-5
        v2=(1+e)*u1/(1+masa);
        v1=v2-e*u1;
        if v1<0
			fi1=pi;
        else
			fi1=0;
        end        
         fi2=0;
    else
%choques no frontales
        fi2=asin(b/2);   %discos iguales de 1 de radio
        if abs(1-e*masa)<1e-5
            angulo=pi/2;
        else
            temp=(1+masa)*tan(fi2)/(1-e*masa);
            angulo=atan(temp);
            if temp<0
                angulo=pi+angulo;
            end
        end
        fi1=angulo-fi2;
        v1=u1*sin(fi2)/sin(fi1+fi2);
        v2=v1*cos(fi1+fi2)+e*u1*cos(fi2);
    end
    v1=abs(v1);
end

m1=1;
u1=3.5;
m2=2;  %partícula 2 en reposo, u2=0
u2=0;
e=0.9; %coeficiente de restitución
b=0.8; %parámetro de impacto

[v1,fi1,v2,fi2]=choque_2(u1,e,b,m2/m1);
fprintf('Velocidad %1.2f de la partícula 1, %3.2f
 dirección\n',v1,fi1*180/pi);
fprintf('Velocidad %1.2f de la partícula 2, %3.2f
 dirección\n',v2,fi2*180/pi);
Q=0.5*(1-e^2)*m1*m2*u1^2*(cos(fi2))^2/(m1+m2);
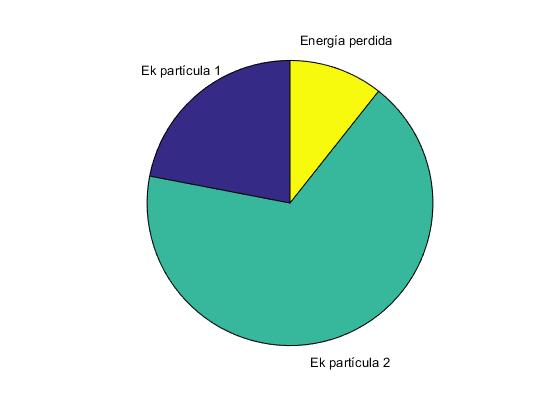
labels = {'Ek partícula 1','Ek partícula 2','Energía perdida'};
X=[m1*v1^2/2,m2*v2^2/2,Q];
pie(X,labels)

Velocidad 1.64 de la partícula 1, 97.85 dirección
Velocidad 2.03 de la partícula 2, 23.58 dirección

En el diagrama de tarta vemos como se reparte la energía inicial del sistema de dos partículas: energía cinética de la primera partícula, energía cinética de la segunda partícula, energía Q perdida en el choque

choques3.gif (907 bytes)

Actividades

Se introduce:

El coeficiente de restitución, en el control titulado Coef. Restitución. Un valor comprendido entre 0 y 1, (el valor de 1 corresponde a un choque elástico)
El parámetro de impacto , en el control titulado P. impacto. Un número comprendido entre 0 y 2, (se supone que las partículas son dos discos de radio unidad). El valor cero corresponde a los choques frontales.
El cociente entre las masas m₂/m₁en el control titulado Cociente masas (m₂/m₁). Donde m₂ es la masa de la partícula que está inicialmente en reposo, y m₁ la masa de la partícula inicialmente en movimiento.
La velocidad de la primera partícula u₁, en el control titulado Velocidad

Se pulsa el botón titulado Nuevo

Observamos el choque en el Sistema-L del laboratorio. Una cruz de color rosa representa la posición del centro de masas del sistema formado por las dos partículas interactuantes. A la izquierda, observamos las energías de las partículas en un diagrama en forma de tarta. Cuando el choque es elástico, la energía inicial es igual a la energía final. Cuando el choque es inelástico (coeficiente de restitución menor que la unidad) la energía inicial es mayor que la final.

Para observar el choque en el Sistema-C activamos el botón de radio titulado S.R. c.m. Para volver al Sistema-L activamos el botón de radio titulado S.R. Lab.

Se proporcionan los datos correspondientes a la velocidad de las partículas antes del choque y después del choque en el Sistema–L, así como las direcciones de las partículas después del choque. Se representan también los momentos lineales en forma de vectores antes del choque y después del choque. De este modo, el lector puede comprobar de forma visual la conservación del momento lineal.

La misma información que se proporciona del choque en el Sistema-L también se proporciona en el Sistema-C.

Velocidad (m/s) Coef. restitución:
Cociente masas (m₂/m₁) P. impacto:
S.R. Lab S.R. c.m.

Referencias

Apartado, Choques elásticos

Carl E Mungan, Trevor C Lipscombe. Oblique elastic collisions of two smooth round objects. Eur. J. Phys. 39 (2018) 045002

Artículo disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017