Modelo unidimensional del movimiento de un cuerpo en el seno de un fluido viscoso
Cuando un cuerpo se mueve en el seno de un fluido experimenta una fuerza de rozamiento que depende de su velocidad, la forma funcional depende del número de Reynolds.
-
Cuando el número de Reynolds es pequeño, la fuerza de rozamiento es proporcional a la velocidad (ley de Stokes).
-
Cuando el número de Reynolds es elevado, la fuerza de rozamiento es proporcional al cuadrado de la velocidad del cuerpo.
La fuerza de rozamiento como vamos a comprobar en esta página, se debe a las colisiones entre el cuerpo y las moléculas del medio.
El modelo unidimensional consta de un cuerpo de masa M y velocidad inicial V0 que choca elásticamente con las partículas del medio inicialmente en reposo, de masas m<M. Las partículas del medio se suponen situadas en una línea recta e igualmente espaciadas tal como se muestra en la figura

Primera colisión
Choque elástico de un cuerpo de masa M y velocidad V0 con una partícula de masa m en reposo

-
Principio de conservación del momento lineal
- Definición del coeficiente de restitución e=1 (elástico)
MV0=MV1+mv1
- V0=V1-v1
En este sistema de dos ecuaciones con dos incógnitas, despajamos la velocidad del cuerpo después del choque V1 y la velocidad de la partícula después del choque v1.
Como v1>V1, la primera partícula del medio choca con una segunda partícula inicialmente en reposo.
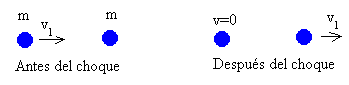
Cuando una partícula de masa m y velocidad v1 choca con una partícula idéntica de masa m en reposo, la primera partícula permanece en reposo después del choque y la segunda partícula, adquiere el momento lineal de la primera.
Este proceso se repite con el resto de las partículas del medio. El momento lineal perdido por el cuerpo en la primera colisión se va transfiriendo de partícula en partícula por medio en los sucesivos choques entre las mismas.
Segunda colisión
El cuerpo que se mueve con velocidad V1 después del primer choque, vuelve a experimentar una segunda colisión con la primera partícula en reposo.
La velocidad del cuerpo V2 y de la primera partícula v2 después del choque son, respectivamente
El cuerpo transfiere una parte de su momento lineal a la primera partícula. Esta partícula que se mueve después del choque, más deprisa v2>V2 que el cuerpo, choca con la segunda partícula en reposo, trasfiriéndole la totalidad de su momento lineal, la segunda partícula choca con la tercera y así, sucesivamente.
N-colisión
El cuerpo va reduciendo su velocidad V2<V1<V0 a la vez que va transfiriendo momento lineal a las partículas del medio.
La velocidad del cuerpo después de N colisiones es
Suponiendo que la densidad (lineal) del medio es ρ uniforme, el número de partículas que hay en una longitud x es ρx. El número de choques que experimenta el cuerpo después de desplazarse una distancia x en el interior del medio es N= ρx, y su velocidad será
La velocidad del cuerpo disminuye exponencialmente con x.
En la figura, se representa la velocidad del cuerpo V/V0 en función de ρ·x para dos valores de r=m/M.
hold on
for r=[0.2,0.8]
k=log((1+r)/(1-r));
fplot(@(x) exp(-k*x),[0,2],'displayName',num2str(r))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('\rho·x')
ylabel('V/V_0')
title('Velocidad')
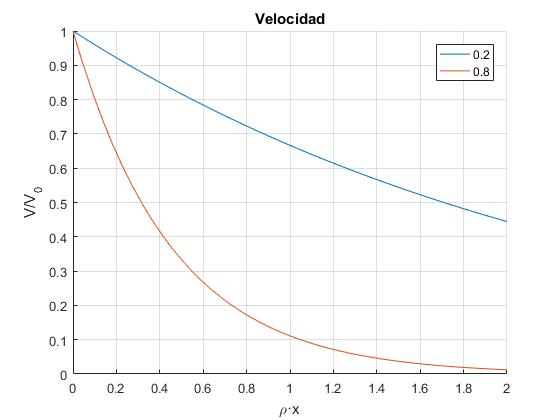
Cuando mayor sea la masa del cuerpo M, (más pequeño r) más penetra en el medio hasta que finalmente se para (teóricamente, cuando x→∞)
La fuerza de rozamiento
La segunda ley de Newton afirma que la fuerza sobre el cuerpo F=Ma
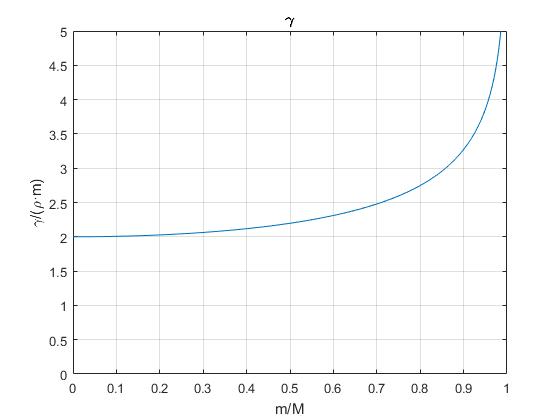
La fuerza de rozamiento F=-γV2 es proporcional al cuadrado de la velocidad V , donde la constante γ de proporcionalidad vale
En la figura, se representa la constante γ en función de r.
fplot(@(x) log((1+x)./(1-x))./x,[eps,1])
ylim([0,5])
grid on
xlabel('m/M')
ylabel('\gamma/(\rho·m)')
title('\gamma')
Actividades
Se introduce
- El cociente r=m/M, en el control titulado Cociente m/M.
- La velocidad inicial del cuerpo se ha fijado en V0=1
Se pulsa el botón titulado Nuevo
Observamos los sucesivos choques entre el cuerpo (color rojo) y la primera partícula del medio (color azul) y los choques entre partículas pintadas de diversos colores.
Se representa la velocidad V del cuerpo en función del desplazamiento x.
Referencias
Molina M. I., Body motion in a one-dimensional resistive medium. Am. J. Phys. 66 (11) November 1998, pp. 973-974

