Choques en un carril
Supongamos dos partículas de masas m1 y m2 que llevan la misma velocidad v0 y se dirigen al final del carril, tal como se muestra en la figura.
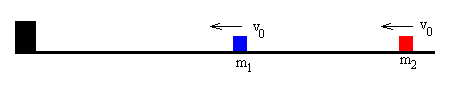
Primero, analizamos por separado los dos fenómenos que pueden ocurrir en esta experiencia:
- Choque de una partícula con el carril
- Choque entre las dos partículas
Choque con el extremo del carril
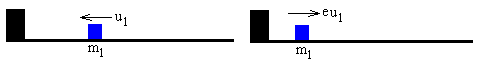
Cuando la partícula de masa m1 que lleva una velocidad u1 choca con el final del carril cambia el sentido y el módulo de su velocidad a v1=-eu1, siendo e el coeficiente de restitución.
Choque de las dos partículas
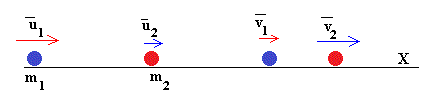
Aplicamos el principio de conservación del momento lineal
m1u1+m2u2=m1v1+m2v2
y de la definición del coeficiente de restitución e
-e(u1-u2)=v1-v2
Despejamos las velocidades después del choque v1 y v2
Movimiento de las partículas
La partícula de masa m1 se dirige hacia el extremo del carril con velocidad -v0, choca y cambia su velocidad a ev0
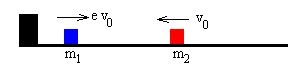
Posteriormente chocan las dos partículas con velocidades iniciales u1=ev0 y u2=-v0
La masa m1 permanece en reposo v1=0 después del choque si
m1=m2(e2+e+1)/e
Si el choque es elástico e=1, m1=3m2, v2=2v0. Toda la energía inicial se transfiere a la partícula de masa m2.
Si el choque no es elástico, por ejemplo e=0.8, m1=3.05m2, v2=1.44v0
Si m1<3m2, la partícula de masa m1 choca una segunda vez con el final del carril. Se aproxima a la partícula m2 con velocidad -ev1
- Si -ev1<v2 no hay más colisiones
- Si -ev1>v2, entonces m1 chocará con m2 una segunda vez, siempre que m1<m2
Las velocidades de las dos partículas después de esta segunda colisión, con u1=-ev1 y u2=v2, son
Cuando e=1, la partícula de masa m1 permanecerá en reposo tras la segunda colisión si m1=0.528 m2
Cuando m1 es pequeña frente a m2, puede experimentar múltiples colisiones con el final del carril y con m2.
Ejemplo:
- Masas de las partículas: m1=0.5 kg, m2=1.0 kg
- Velocidades iniciales: u1=-1.0 m/s, u2=-1.0 m/s
- Coeficiente de restitución: e=0.8
La partícula m1 choca con el final del carril y rebota con velocidad
v1=-eu1=0.8 m/s
Esta es la velocidad inicial u1=0.8 de la partícula m1 cuando choca con la partícula m2
Las velocidades después del primer choque son:
La partícula m1 se dirige hacia el final del carril y rebota con velocidad u1=-ev1=1.088 m/s
La partícula m1 choca por segunda vez con la partícula m2 cuya velocidad inicial u2=0.08 m/s
La partícula m1 se dirige hacia el final del carril y rebota con velocidad u1=-ev1=0.0973m/s
Ahora, ambas partículas se dirigen a lo largo del eje X hacia la derecha, la velocidad de m1 (0.0973) es menor que la velocidad de m2 (0.6848) por lo que ya no hay más choques. Estas son las velocidades finales de las dos partículas.
La energía inicial y final del sistema formado por las dos partículas es
Se ha perdido energía en los sucesivos choques entre las partículas y de la primera con el final del carril.
Actividades
Se introduce
- El cociente m1/m2 de las masas de las dos partículas, en el control titulado Cociente m1/m2
- El coeficiente de restitución e, en el control titulado Coeficiente restitución
- La velocidad inicial de las dos partículas se ha fijado en u1=-1.0 m/s y u2=-1.0 m/s
Se pulsa el botón titulado Nuevo.
Observamos los choques de la primera partícula contra el final del carril y el choque entre las dos partículas.
Los datos de las velocidades de las dos partículas aparecen en la parte superior.
Una barra dividida nos indica:
- La energía cinética de la primera partícula (en color azul)
- La energía cinética de la segunda partícula (en color rojo)
- El resto, hasta completar la barra, es la energía perdida en los choques.
Cuando el choque es elástico, e=1, la energía inicial es igual a la final.
Choques elásticos
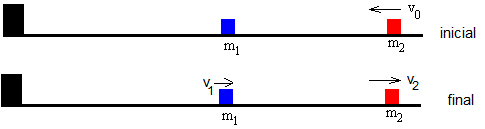
Supongamos que la partícula 1 está inicialmente en reposo a una distancia del extremo del carril y la partícula 2 se le proporciona una velocidad v0<0. La secuencia es:
- choque de 2 con 1
- rebote de 1 en el extremo del carril
- choque de 2 con 1
- rebote de 1
- ....
hasta que las velocidades v1 y v2 son ambas positivas, alejándose del extremo del carril.
- Si v1<v2 se habrán producido n choques y n rebotes
- Si v1>v2 tendrá lugar, un choque adicional
Vamos a determinar el número de choques entre las dos partículas y de rebotes de la primera con el extremo del carril en función del parámetro k=(m2-m1)/(m2+m1), relacionado con las masas de las partículas
Choque elástico entre las dos partículas

Cuando el choque es elástico, el coeficiente de restitución e=1.
Las velocidades de las partículas antes del choque son u1 y u2. Después del choque elástico las velocidades v1 y v2 de las partículas serán
La partícula de masa m2 se mueve inicialmente con velocidad u2=-v0 hacia la izquierda y la partícula de masa m1 está en reposo. Para que se mueva en el mismo sentido después del choque, v2<0 la masa m2>m1. Cuando m2=m1, la partícula de masa m2 se detiene, v2=0 y la partícula de masa m1 adquiere la velocidad inicial v0.
Expresamos las ecuaciones en forma matricial y definimos la matriz S del choque
con 0≤k≤1
v=S·u
Rebote con el exteremo del carril
La partícula de masa m1 rebota elásticamente en el extremo del carril, invirtiendo el sentido de su velocidad de -v1 a v1
Definimos la matriz de rebote R, que afecta solamente a la velocidad v1 de la primera partícula, v'=R·v, dejando la segunda v2 inalterada
n choques y n rebotes
Después de n choques y n rebotes, las velocidades de las partículas serán
v'=(RS)(RS)....(RS)v0=(RS)nv0
Las propiedades de las matrices S y R son
R·R=I (matriz unidad)
>> syms k;
>> R=[-1,0;0,1];
>> R*R
ans
1 0
0 1
S·S=I
>> S=[-k,1+k;1-k,k]; >> >> simplify(S*S) ans = [ 1, 0] [ 0, 1]
(R·S)·(S·R)=I
>> simplify((R*S)*(S*R)) ans = [ 1, 0] [ 0, 1]
Un resultado importante, R·S+S·R=2k·I
>> R*S+S*R ans = [ 2*k, 0] [ 0, 2*k]
Despejamos el producto (R·S)
Elevamos (R·S) al cuadrado
- Elevamos (R·S) al cubo
- Elevamos (R·S) a al cuarta potencia
- Elevamos (R·S) a al quinta potencia
.....
En el paréntesis de la izquierda vemos los polinomios de Chebyshev de segunda especie Un(x) y en el de la derecha Un-1(x)
La partícula 1 está inicialmente en reposo y la 2 se dirige hacia la pared con velocidad v0<0. Las velocidades finales de las partículas v1 y v2 después de n choques y n rebotes con el extremo del carril, son
Si después de n choques y n rebotes, las velocidades finales son positivas, v1>0, v2>0, pueden ocurrir dos casos:
Si v1<v2, las partículas ya no vuelven a interaccionar, v1 y v2 son las velocidades finales
Si v1>v2, las partículas experimentan un choque adicional, las velocidades finales v1 y v2 se calculan del siguiente modo:
Número de choques y número de rebotes en función del parámetro k
Para representar gráficamente un polinomio Un(x), utilizaremos la función recursiva
function y=chebyshev_2(n,x) %n=0,1,2,3...
if n==0
y=ones(1,length(x));
elseif n==1
y=2*x;
else
y=2*x.*chebyshev_2(n-1,x)-chebyshev_2(n-2,x);
end
end
Para calcular mediante roots de MATLAB las raíces de un polinomio Un(x), utilizaremos la función
function p=chebypoly_2(n) %n es grado 1,2...
p=zeros(n,1);
p0=[0];
p1=[1];
for i=2:n+1
p=2*[p1,0]-[0,p0];
p0=[0,p1];
p1=p;
end
end
Ambas funciones se han definido en la página titulada Polinomios de Chebyshev
En el programa interactivo al final de esta página, observamos que cuando k es pequeño se producen dos choques y dos rebotes
n=2, dos rebotes y dos choques
Representamos v1 y v2 en función de k, para n choques y n rebotes
%n choques y n rebotes
hold on
n=2;
v0=-1; %velocidad inicial
v1=@(x) -(x+1).*chebyshev_2(n-1,x)*v0;
v2=@(x) (chebyshev_2(n,x)-x.*chebyshev_2(n-1,x))*v0;
fplot(v1,[0,1])
fplot(v2,[0,1])
title(sprintf('choques=%i, rebotes=%i',n,n))
legend('1','2','location','northwest')
xlabel('k')
ylabel('y')
grid on
hold off
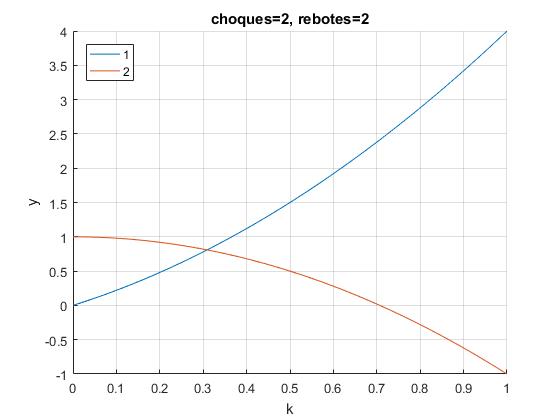
Las velocidades finales v1>0 y v2>0 son positivas para valores de k<0.5, pero v1>v2 para un valor de k próximo a 0.3
Calculamos este valor límite, cuando v1=v2, es decir, cuando Un(k)+Un-1(k)=0, con n=2.
n=2; %n choques y n rebotes p=chebypoly_2(n); p1=chebypoly_2(n-1); x=roots(p+[0,p1]); disp(x')
-0.8090 0.3090
La raíz mayor positiva es k1=0.3090, se puede calcular de forma alternativa, utilizando la representación trigonométrica de los polinomios de Chebyshev
>> n=2; >> k1=cos(2*pi/(2*n+1)) k1 = 0.3090
En el intervalo (0, 0.3090) se producen dos choques y dos rebotes. Por ejemplo, para k=0.2, el programa interactivo da unas velocidades finales v1=0.48 y v2=0.92, que coinciden con las calculadas
>> v1(0.2) ans = 0.4800 >> v2(0.2) ans = 0.9200
n=2+½, dos rebotes y tres choques
Representamos v1 y v2 en función de k, para n+1 choques y n rebotes
%n+1 choques y n rebotes
hold on
n=2;
v0=-1; %velocidad inicial
v1=@(x) (x+1).*chebyshev_2(n,x)*v0;
v2=@(x) (x.*chebyshev_2(n,x)-chebyshev_2(n-1,x))*v0;
fplot(v1,[0,1])
fplot(v2,[0,1])
title(sprintf('choques=%i, rebotes=%i',n+1,n))
legend('1','2','location','northwest')
xlabel('k')
ylabel('y')
grid on
hold off
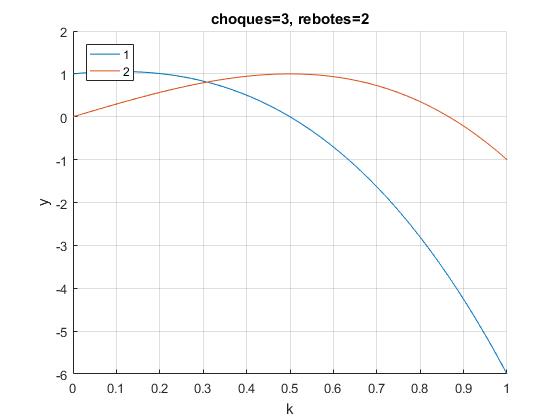
Las velocidades finales v1>0, v2>0 y v1<v2 para valores de k comprendidos entre 0.3090 y 0.5, pero v1<0 a partir de este límite, que es la raíz mayor positiva de U2(k)
n=2; %n+1 choques y n rebotes p=chebypoly_2(n); x=roots(p); disp(x')
0.5000 -0.5000
La raíz mayor positiva k2=0.5, se puede calcular de forma alternativa, utilizando la representación trigonométrica de los polinomios de Chebyshev
El valor mayor de k corresponde al menor ángulo θm, para m=1
>> n=2; >> cos(pi/(n+1)) ans = 0.5000
En el intervalo (0.3090, 0.5) se producen tres choques y dos rebotes. Por ejemplo, para k=0.4, el programa interactivo da unas velocidades finales v1=0.504 y v2=0.944, que coinciden con las calculadas
>> v1(0.4) ans = 0.5040 >> v2(0.4) ans = 0.9440
n=3, tres rebotes y tres choques
Representamos v1 y v2 en función de k, para n choques y n rebotes
%n choques y n rebotes
hold on
n=3; %número de choques
v0=-1; %velocidad inicial
v1=@(x) -(x+1).*chebyshev_2(n-1,x)*v0;
v2=@(x) (chebyshev_2(n,x)-x.*chebyshev_2(n-1,x))*v0;
fplot(v1,[0,1])
fplot(v2,[0,1])
title(sprintf('choques=%i, rebotes=%i',n,n))
legend('1','2','location','northwest')
xlabel('k')
ylabel('y')
grid on
hold off
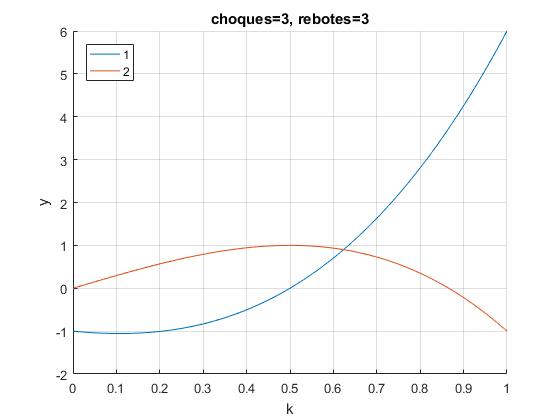
Las velocidades finales v1>0 y v2>0 son positivas para valores de k>0.5, pero v1>v2 para un valor de k próximo a 0.6
Calculamos este valor límite, cuando v1=v2, es decir, cuando Un(k)+Un-1(k)=0, con n=3.
n=3; %n choques y n rebotes p=chebypoly_2(n); p1=chebypoly_2(n-1); x=roots(p+[0,p1]); disp(x')
-0.9010 0.6235 -0.2225
La raíz mayor positiva es k3=0.3090, se puede calcular de forma alternativa, utilizando la representación trigonométrica de los polinomios de Chebyshev, Un(k)=-Un-1(k)
>> n=3; >> k3=cos(2*pi/(2*n+1)) k3 = 0.6235
En el intervalo (0.5, 0.6235) se producen n=3, tres choques y tres rebotes. Por ejemplo, para k=0.6, el programa interactivo da unas velocidades finales v1=0.704 y v2=0.936, que coinciden con las calculadas
>> v1(0.6) ans = 0.7040 >> v2(0.6) ans = 0.9360
n=3+½, tres rebotes y cuatro choques
Representamos v1 y v2 en función de k, para n+1 choques y n rebotes
%n+1 choques y n rebotes
hold on
n=3;
v0=-1; %velocidad inicial
v1=@(x) (x+1).*chebyshev_2(n,x)*v0;
v2=@(x) (x.*chebyshev_2(n,x)-chebyshev_2(n-1,x))*v0;
fplot(v1,[0,1])
fplot(v2,[0,1])
title(sprintf('choques=%i, rebotes=%i',n+1,n))
legend('1','2','location','northwest')
xlabel('k')
ylabel('y')
grid on
hold off
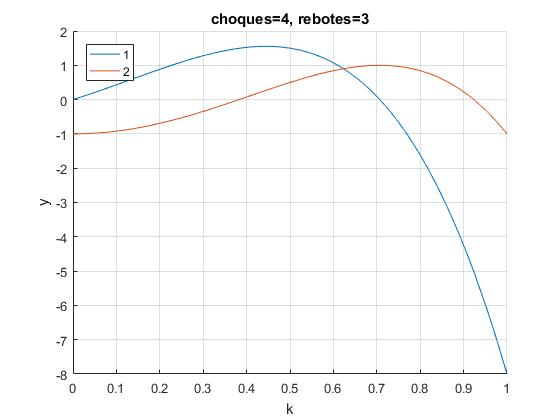
Las velocidades finales v1>0, v2>0 y v1<v2 para valores de k comprendidos entre 0.6235 y 0.7, pero v1<0 a partir de este límite, que es la raíz mayor positiva de U3(k)
n=3; %n+1 choques y n rebotes p=chebypoly_2(n); x=roots(p); disp(x')
0 0.7071 -0.7071
La raíz mayor positiva k4=0.7071, se puede calcular de forma alternativa, utilizando la representación trigonométrica de los polinomios de Chebyshev
>> n=3; >> cos(pi/(n+1)) ans = 0.7071
En el intervalo (0.6235, 0.7071) se producen cuatro choques y tres rebotes. Por ejemplo, para k=0.65, el programa interactivo da unas velocidades finales v1=0.665 y v2=0.952, que coinciden con las calculadas
>> v1(0.65) ans = 0.6649 >> v2(0.65) ans = 0.9520
y así, sucesivamente...
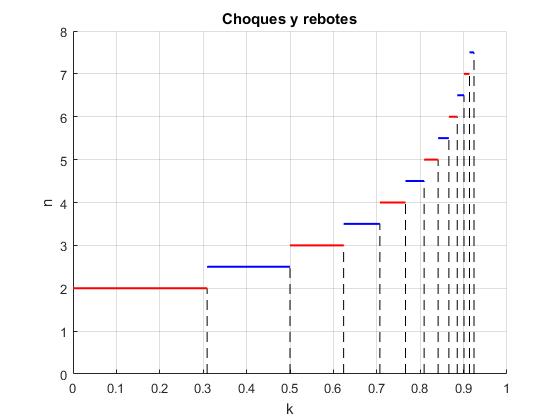
Creamos un script, para representar en el eje horizontal el parámetro 0≤k≤1, y en el eje vertical n el número de rebotes y choques. n+½ significa n+1 choques y n rebotes
k1=0;
for n=2:7
%n choques y n rebotes
k=cos(2*pi/(2*n+1)); %raíz
line([k,k],[0,n],'lineStyle','--','color','k')
line([k1,k],[n,n],'lineWidth',1.5,'color','r')
k1=k;
%n+1 choques y n rebotes
k=cos(pi/(n+1));
line([k,k],[0,n+1/2],'lineStyle','--','color','k')
line([k1,k],[n+1/2,n+1/2],'lineWidth',1.5,'color','b')
k1=k;
end
grid on
xlabel('k')
ylabel('n')
title('Choques y rebotes')
El número π
Cuando m2/m1=102,104,106..., o bien, cuando
El número n de colisiones y n rebotes, en total 2n, se acerca a un múltiplo de π
format long g
for m2_1=[1,1e2,1e4,1e6,1e8, 1e10]
k=(m2_1-1)/(m2_1+1);
N=2*pi/acos(k)-1; %choques y rebotes
disp([m2_1,round(N)/sqrt(m2_1)])
end
1 3
100 3.1
10000 3.13
1000000 3.141
100000000 3.1415
10000000000 3.14158
Probamos en el programa interactivo, más abajo, m2/m1=100 o bien, k=0.980198, obtenemos 16+15=31 choques y rebotes. Ahora, con m2/m1=10 000 o bien, k=0.99980002, obtenemos 157+157=314 choques y rebotes. Como vemos se precisa un cociente m2/m1 muy grande para obtener apenas unos pocos decimales de π
Actividades
Se introduce
- El parámetro k=(m2-m1)/(m2+m1), en el intervalo (0,1) en el control titulado Parámetro k
Se pulsa el botón titulado Nuevo
En la parte superior derecha, se muestra el número de choques y rebotes. En la parte, superior, las velocidades de las partículas v1 y v2
Comprobar que cuando se introduce en el control los valores límites de k: 0.309, 0.5, 0.6235, 0.7071..., la primera partícula finaliza su movimiento en reposo
Referencias
De este último apartado
J. R. Drugowich, Felicio D. M. Redondo. Linear collisions revisited. Am. J. Phys. 49(2) Feb. 1981 pp. 147-151

