Secuencia de colisiones de tres partículas

Choque de dos partículas de la misma masa

Aplicamos el principio de conservación del momento lineal al sistema aislado formado por dos partículas de la misma masa m y con velocidades iniciales u y u' de la misma dirección y sentido. Supondremos que u>u'

mu+mu'=mv+mv'

y de la definición del coeficiente de restitución e

-e(u-u')=v-v'

Despejamos las velocidades v y v' después del choque

$v = \frac{(1 - e) u + (1 + e) u'}{2} v' = \frac{(1 + e) u + (1 - e) u'}{2}$

En forma matricial

$(\begin{matrix} v \\ v' \end{matrix}) = \frac{1}{2} (\begin{matrix} 1 - e & 1 + e \\ 1 + e & 1 - e \end{matrix}) (\begin{matrix} u \\ u' \end{matrix})$

Secuencia de colisiones

Consideramos un ciclo completo, cuando chocan la primera y la segunda partícula y a continuación, la segunda con la tercera

Un nuevo ciclo se podría repetir si vuelven a chocar la primera y segunda partícula

Determinaremos el valor del coeficiente de restitución e crítico para que se complete un ciclo o para que se repita

1.-Primer ciclo

La primera partícula choca con la segunda, sus velocidades iniciales y finales son, respectivamente.

${\begin{cases} u_{1} = 1 \\ u_{2} = 0 \end{cases} {\begin{cases} v_{1} = \frac{1}{2} (1 - e) \\ v_{2} = \frac{1}{2} (1 + e) \end{cases}$

>> syms e;
>> M=[1-e,1+e;1+e,1-e]/2;
>> V=M*[1;0];
>> v1=V(1)
v1 =1/2 - e/2
>> v2=V(2)
v2 =e/2 + 1/2

La segunda partícula choca con la tercera, sus velocidades iniciales y finales son, respectivamente.

${\begin{cases} u_{2} = \frac{1}{2} (1 + e) \\ u_{3} = 0 \end{cases} {\begin{cases} v_{2} = \frac{1}{4} (1 - e^{2}) \\ v_{3} = \frac{1}{4} {(1 + e)}^{2} \end{cases}$

>> V=M*[v2;0];
>> v2=V(1)
v2 =-(e/2 - 1/2)*(e/2 + 1/2)
>> v3=V(2)
v3 =(e/2 + 1/2)^2

La velocidad de la primera partícula u₁=(1-e)/2 es mayor que la de la segunda, u₂=(1-e²)/4 por lo que vuelven a chocar, completándose el primer ciclo

$\begin{array}{l} \frac{1}{2} (1 - e) > \frac{1}{4} (1 - e^{2}) \\ 2 > 1 + e \end{array}$

Como e<1 se cumple la desigualdad

2.-Segundo ciclo

La primera partícula choca con la segunda, sus velocidades iniciales y finales son, respectivamente.

${\begin{cases} u_{1} = \frac{1}{2} (1 - e) \\ u_{2} = \frac{1}{4} (1 - e^{2}) \end{cases} {\begin{cases} v_{1} = \frac{1}{8} (1 - e) (3 + e^{2}) \\ v_{2} = \frac{1}{8} (1 - e) (1 + e) (3 - e) \end{cases}$

>> V=M*[v1;v2];
v1=collect(V(1))
v1 =- e^3/8 + e^2/8 - (3*e)/8 + 3/8
>> factor(v1)
ans =[ -1/8, e - 1, e^2 + 3]
>> v2=collect(V(2))
v2 =e^3/8 - (3*e^2)/8 - e/8 + 3/8
>> factor(v2)
ans =[ 1/8, e - 3, e - 1, e + 1]

La segunda y tercera partícula chocan si u₂>u₃, y esto se produce siempre que el coeficiente de restitución e sea menor que cierto valor crítico

$\begin{array}{l} \frac{1}{8} (1 - e) (1 + e) (3 - e) > \frac{1}{4} {(1 + e)}^{2} \\ e^{2} - 6 e + 1 > 0 \\ (e - 3 + 2 \sqrt{2}) (e - 3 - 2 \sqrt{2}) > 0 \\ e \leq 3 - 2 \sqrt{2} \end{array}$

Si se cumple esta condición, e≤0.1716, la segunda partícula choca con la tercera, sus velocidades iniciales y finales son, respectivamente.

${\begin{cases} u_{2} = \frac{1}{8} (1 - e) (1 + e) (3 - e) \\ u_{3} = \frac{1}{4} {(1 + e)}^{2} \end{cases} {\begin{cases} v_{2} = \frac{1}{16} (5 - 3 e + 7 e^{2} - e^{3}) (1 + e) \\ v_{3} = \frac{1}{16} {(1 + e)}^{2} (1 - e) (5 - e) \end{cases}$

>> V=M*[v2;v3];
>> v2=collect(V(1))16*collect
v2 =- e^4/16 + (3*e^3)/8 + e^2/4 + e/8 + 5/16
>> factor(v2)
ans =[ -1/16, e + 1, e^3 - 7*e^2 + 3*e - 5]
>> v3=collect(V(2))
v3 =e^4/16 - e^3/4 - (3*e^2)/8 + e/4 + 5/16
>> factor(v3)
ans =[ 1/16, e - 1, e - 5, e + 1, e + 1]

Se completaría el segundo ciclo, si la primera y segunda partícula volviesen a chocar, u₁>u₂, para ello el coeficiente de restitución tiene que ser menor que cierto valor crítico

$\begin{array}{l} \frac{1}{8} (1 - e) (3 + e^{2}) > \frac{1}{16} (5 - 3 e + 7 e^{2} - e^{3}) (1 + e) \\ e^{4} - 8 e^{3} - 2 e^{2} - 8 e + 10 > 0 \end{array}$

>> 16*collect(v1-v2)
 ans =e^4 - 8*e^3 - 2*e^2 - 8*e + 1
>> roots([1,-8,-2,-8,1])
ans =
   8.3524 + 0.0000i
  -0.2361 + 0.9717i
  -0.2361 - 0.9717i
   0.1197 + 0.0000i

La menor raíz real positiva es e=0.1197

Si se cumple la condición, e≤0.1197, la primera partícula choca con la segunda, completándose el segundo ciclo.

3.-Tercer ciclo

La primera partícula choca con la segunda, sus velocidades iniciales y finales son, respectivamente.

${\begin{cases} u_{1} = \frac{1}{8} (1 - e) (3 + e^{2}) \\ u_{2} = \frac{1}{16} (5 - 3 e + 7 e^{2} - e^{3}) (1 + e) \end{cases} {\begin{cases} v_{1} = \frac{1}{32} (- e^{5} + 7 e^{4} + 6 e^{3} + 14 e^{2} - 5 e + 11) \\ v_{2} = \frac{1}{32} (e^{5} - 9 e^{4} + 2 e^{3} - 2 e^{2} - 3 e + 11) \end{cases}$

>> V=M*[v1;v2];
>> v1=collect(V(1))
v1 =- e^5/32 + (7*e^4)/32 + (3*e^3)/16 + (7*e^2)/16 - (5*e)/32 + 11/32
>> v2=collect(V(2))
v2 =e^5/32 - (9*e^4)/32 + e^3/16 - e^2/16 - (3*e)/32 + 11/32

La segunda y tercera partícula chocan si u₂>u₃, y esto se produce siempre que el coeficiente de restitución e sea menor que cierto valor crítico

>> 32*collect(v2-v3)
 ans =e^5 - 11*e^4 + 10*e^3 + 10*e^2 - 11*e + 1
 >> roots([1,-11,10,10,-11,1])
ans =
   9.8990 + 0.0000i
  -1.0000 + 0.0000i
   1.0000 + 0.0000i
   1.0000 - 0.0000i
   0.1010 + 0.0000i

La menor raíz real positiva es e=0.1010

Si se cumple la condición, e≤0.1010, la segunda partícula choca con la tercera, sus velocidades iniciales y finales son, respectivamente

$\begin{array}{l} {\begin{cases} u_{2} = \frac{1}{32} (e^{5} - 9 e^{4} + 2 e^{3} - 2 e^{2} - 3 e + 11) \\ u_{3} = \frac{1}{16} {(1 + e)}^{2} (1 - e) (5 - e) \end{cases} \\ {\begin{cases} v_{2} = \frac{1}{64} (- e^{6} + 12 e^{5} - 17 e^{4} - 16 e^{3} - 3 e^{2} + 4 e + 21) \\ v_{3} = \frac{1}{64} (e^{6} - 10 e^{5} + 3 e^{4} + 4 e^{3} - 25 e^{2} + 6 e + 21) \end{cases} \end{array}$

Se completaría el tercer ciclo, si la primera y segunda partícula volviesen a chocar, u₁>u₂, para ello el coeficiente de restitución tiene que ser menor que cierto valor crítico

>> 64*collect(v2-v1)
ans =- e^6 + 14*e^5 - 31*e^4 - 28*e^3 - 31*e^2 + 14*e - 1
>> coef=sym2poly(v1-v2)*64
coef =     1   -14    31    28    31   -14     1
>> roots(coef)
ans =
  10.8961 + 0.0000i
   3.9678 + 0.0000i
  -0.6039 + 0.7971i
  -0.6039 - 0.7971i
   0.2520 + 0.0000i
   0.0918 + 0.0000i

La menor raíz real positiva es e=0.0918

Si se cumple la condición, e≤0.0918, la primera partícula choca con la segunda, completándose el tercer ciclo.

y así sucesivamente...

Comprobamos que se conserva el momento lineal

>>> simplify(v1+v2+v3)
ans =1

...-n ciclo

Reunimos las porciones de código en un solo script

format compact;
syms e; %coeficiente de restitución
%Matriz de choque
M=[1-e,1+e;1+e,1-e]/2;
%primer choque de la partícula 1 con la 2
    V=M*[1;0];
    disp('1.-choque 1-->2')
    v1=collect(V(1))
    v2=collect(V(2))
%choque de la partícula 2 con la 3
    V=M*[v2;0];
    disp('1.-choque 2-->3')
    v2=collect(V(1))
    v3=collect(V(2))
%Sucesivos choques
for i=1:5
%choque de 1 con 2
    V=M*[v1;v2];
    fprintf('%1i .-choque 1-->2\n',i+1)
    v1=collect(V(1))
    v2=collect(V(2))
    r=roots((sym2poly(v2-v3)));
    e1=min(abs(r));
    veloc=subs(v2,e,e1);
    fprintf('choque 1 y 2 si: e<%1.4f, v=%1.4f\n',e1,veloc)
 %choque de 2 con 3
    V=M*[v2;v3];
    fprintf('%1i .-choque 2-->3\n',i+1)
    v2=collect(V(1))
    v3=collect(V(2))
    r=roots((sym2poly(v1-v2)));
    e1=min(abs(r));
    veloc=subs(v2,e,e1);
    fprintf('choque 1 y 2 si: e<%1.4f, v=%1.4f\n',e1,veloc)
end

1.-choque 1-->2
v1 =1/2 - e/2
v2 =e/2 + 1/2
1.-choque 2-->3
v2 =1/4 - e^2/4
v3 =e^2/4 + e/2 + 1/4
2 .-choque 1-->2
v1 =- e^3/8 + e^2/8 - (3*e)/8 + 3/8
v2 =e^3/8 - (3*e^2)/8 - e/8 + 3/8
choque 1 y 2 si: e<0.1716, v=0.3431
2 .-choque 2-->3
v2 =- e^4/16 + (3*e^3)/8 + e^2/4 + e/8 + 5/16
v3 =e^4/16 - e^3/4 - (3*e^2)/8 + e/4 + 5/16
choque 1 y 2 si: e<0.1197, v=0.3317
3 .-choque 1-->2
v1 =- e^5/32 + (7*e^4)/32 + (3*e^3)/16 + (7*e^2)/16 - (5*e)/32 + 11/32
v2 =e^5/32 - (9*e^4)/32 + e^3/16 - e^2/16 - (3*e)/32 + 11/32
choque 1 y 2 si: e<0.1010, v=0.3337
3 .-choque 2-->3
v2 =- e^6/64 + (3*e^5)/16 - (17*e^4)/64 - e^3/4 - (3*e^2)/64 + e/16 + 21/64
v3 =e^6/64 - (5*e^5)/32 + (3*e^4)/64 + e^3/16 - (25*e^2)/64 + (3*e)/32 + 21/64
choque 1 y 2 si: e<0.0918, v=0.3333
4 .-choque 1-->2
v1 =- e^7/128 + (13*e^6)/128 - (21*e^5)/128 - (31*e^4)/128 - (35*e^3)/128 
+ (39*e^2)/128 - (7*e)/128 + 43/128
v2 =e^7/128 - (15*e^6)/128 + (41*e^5)/128 + (25*e^4)/128 + (27*e^3)/128 
+ (11*e^2)/128 - (5*e)/128 + 43/128
choque 1 y 2 si: e<0.0864, v=0.3334
4 .-choque 2-->3
v2=...
v3=....
choque 1 y 2 si: e<0.0830, v=0.3333
5 .-choque 1-->2
v1 =...
v2 =...
choque 1 y 2 si: e<0.0807, v=0.3333
5 .-choque 2-->3
v2 =...
v3 =...
choque 1 y 2 si: e<0.0790, v=0.3333
6 .-choque 1-->2
v1 =...
v2 =...
choque 1 y 2 si: e<0.0778, v=0.3333
6 .-choque 2-->3
v2 =...
v3 =...
choque 1 y 2 si: e<0.0769, v=0.3333

La sucesión de valores críticos del coeficiente de restitución (señalados con letra negrita) son: 0.1716, 0.1197, 0.1010, 0.0918, 0.0864, 0.0830, 0.0807,0.0790, 0.0778, 0.0769...

Representamos las velocidades finales v₁, v₂ y v₃ de las tres partículas en función del coeficiente de restitución e

%datos de los valores críticos del coeficiente de restitución, 
%obtenidos en con el script anterior
ec=[0.1716, 0.1197, 0.1010, 0.0918, 0.0864, 0.0830, 0.0807,0.0790, 0.0778,
 0.0769];
vel=[0.3431, 0.3317, 0.3337, 0.3333, 0.3334, 0.3333, 0.3333, 0.3333, 0.3333,
 0.3333];

j=1; %contador
restitucion=linspace(0.07,0.18,300);
u=zeros(length(restitucion),3);
%n=zeros(length(restitucion),1);
for e=restitucion; %coeficiente de restituación
%situación inicial
    v1=1; v2=0; v3=0; %velocidades
    M=[1-e,1+e;1+e,1-e]/2;
%primer choque de la partícula 1 con la 2
    V=M*[v1;v2];
    v1=V(1); v2=V(2);    
%choque de la partícula 2 con la 3
    V=M*[v2;v3];
    v2=V(1); v3=V(2);
%Sucesivos choques
    for i=1:100
 %choque de 1 con 2
        V=M*[v1;v2];
        v1=V(1); v2=V(2);    
        if v3>v2 %no choca la 2 y la 3
            break;
        end  
%choque de 2 con 3
        V=M*[v2;v3];
        v2=V(1); v3=V(2);
        if v1<v2 %no choca la 1 y la 2
            break;
        end
    end
    u(j,1)=v1;u(j,2)=v2;u(j,3)=v3;
   %n(j)=i;
    j=j+1;
end
hold on
plot(ec,vel,'o','markersize',3,'markeredgecolor','k','markerfacecolor','k')
plot(restitucion,u(:,1),restitucion,u(:,2),restitucion,u(:,3))
hold off
legend('e','1','2','3', 'location','northwest')
grid on
xlabel('e')
ylabel('v')
title('choques')

La gráfica completa, e<1.

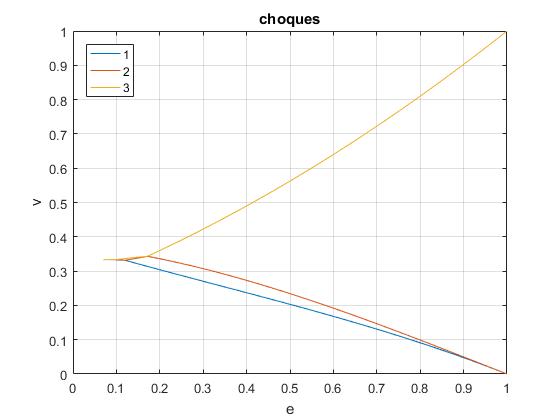
La región de interés, alrededor de e=0.1. Como vemos en esta gráfica, v₂ y v₃ coinciden para e=0.1716, v₁ y v₂ coinciden para e=0.1197, v₂ y v₃ coinciden para e=0.1010, y así, sucesivamente

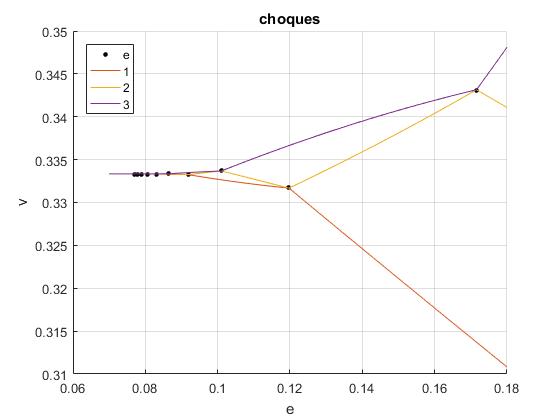
Como podemos apreciar, las velocidades finales de las partículas cumplen que v₁≤v₂≤v₃

Cuando el coeficiente de restitución es pequeño, menor que 0.1, las tres partículas tienen aproximadamente la misma velocidad, 1/3

Referencias

Arne Nordmark, Hanno Essén. An impacting linear three body system. Eur. J. Phys. 39(2018) 015001