Vehículo propulsado por la lluvia
Consideremos un vehículo en forma de prisma cuya base es un triángulo rectángulo de ángulo θ, que puede moverse sin rozamiento sobre una pista horizontal. La lluvia cae verticalmente con velocidad constante u. Las gotas de lluvia chocan elásticamente sobre la superficie frontal vertical A=Bsinθ y la superficie inclinada de área B.
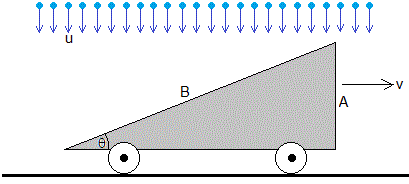
Vamos a determinar la fuerza que ejerce la lluvia sobre las dos superficies y después, formularemos la ecuación del movimiento
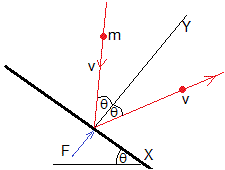
Cuando una partícula de masa m choca elásticamente con un plano inclinado un ángulo θ, la componente de la velocidad a lo largo del plano inclinado (eje X) no cambia. La componente de la velocidad a lo largo del eje Y (perpendicular al plano) cambia de -vcosθ a vcosθ, es decir, 2vcosθ.
El momento lineal de la partícula cambia 2m·vcosθ, y para ello, el plano inclinado ejerce una fuerza F sobre la partícula. La partícula al chocar ejerce una fuerza F sobre el plano inclinado en sentido contrario
Sistema de referencia del vehículo
Nos situamos en el vehículo que viaja a velocidad v
Fuerza sobre la cara frontal vertical de área A.
Fuerza sobre la cara inclinada de área B.
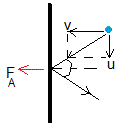
El cambio de velocidad que experimenta la gota de agua al chocar con la cara vertical es 2v
La masa de agua que impacta sobre la cara frontal de área A en la unidad de tiempo es (ρAv). La fuerza que ejerce la lluvia sobre la cara frontal vertical es
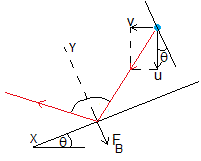
En el choque de la gota con el plano inclinado, la componente de la velocidad a lo largo del eje X no cambia. Sin embargo, cambia la componente de la velocidad a lo largo del eje Y (perpendicular al plano inclinado) de -v⊥ a v⊥
La masa de agua que impacta sobre la cara inclinada de área B en la unidad de tiempo es (ρBV). La fuerza que ejerce la lluvia sobre la cara inclinada es
Ecuación del movimiento
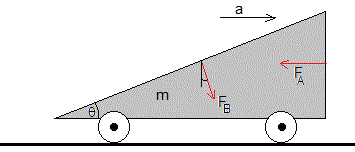
Las fuerzas sobre el vehículo de masa m son FB y FA
El peso y la reacción de la pista no contribuyen al movimiento
La ecuación del movimiento es
Definimos la variable adimensional V=v/u
Definimos la variable adimensional τ
De este modo, expresamos la ecuación diferencial en términos de dos variables adimensionales: V y τ
Integramos esta ecuación sabiendo que en el instante t=0, v=0, parte del reposo
Es una integral del tipo
El resultado es la ecuación
Teniendo en cuenta la relación,
despejamos la velocidad V en función del tiempo τ
Cuando el tiempo τ se hace grande, la velocidad V tiende a
>> syms x; >> limit(coth(x),x, inf) ans =1
Representamos la velocidad V en función del tiempo τ para una inclinación θ=π/4 (45°)
th=pi/4; %plano inclinado 45
V=@(t) cos(th)./(coth(t/cos(th))+sin(th));
fplot(V,[0,4])
grid on
xlabel('\tau')
ylabel('V')
title('Velocidad')
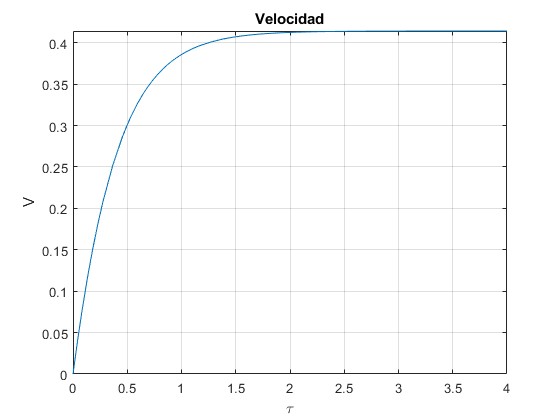
La velocidad límite V∞ es
>> V_f=cos(th)/(1+sin(th)) V_f = 0.4142
Retornando a las variables físicas, la velocidad v en función del tiempo t es
Cuando el tiempo t se hace grande la velocidad v tiende a
Que es la misma ecuación que obtendríamos de la ecuación del movimiento cuando la aceleración es nula
Ejemplo
Velocidad terminal de caída de las gotas de lluvia, u=5 m/s
Densidad lluvia
Densidad del vehículo, ρc=500 kg/m3
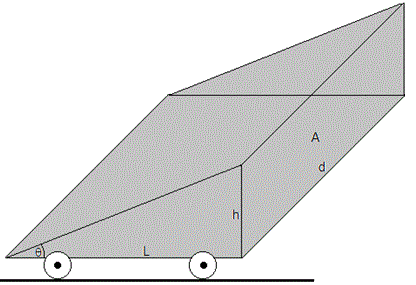
Cociente A/m, área frontal vertical/masa
Longitud del vehículo L=0.2 m
Inclinación θ=π/4 (45°)
La densidad de la lluvia no es la densidad del agua ρa=1000 kg/m3 es mucho menor. Supondremos que la lluvia es uniforme en toda la longitud de pista que recorre el vehículo y que la velocidad terminal de las gotas es la misma u
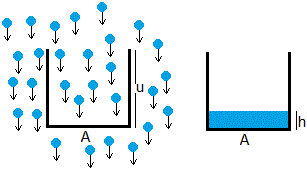
En la unidad de tiempo, un cilindro de área de la base A y de altura u, contiene una masa de agua ρ(Au). Que equivale a la masa de agua de todas las gotas que contiene, ρa(Ah)
Si h=7·10-6 m/s, ρ=7·10-3/5 kg/m3
>> v=@(t) 5*sqrt(2)/(2*coth(14e-5*sqrt(2)*t)+sqrt(2)); >> v(84*60) ans = 1.7488 >> 5*sqrt(2)/(2+sqrt(2)) ans = 2.0711
Para t=84 minutos, v= 1.7488 m/s
La velocidad límite, v∞=2.0711 m/s
Referencias
Carl E Mungan, Trevor C Lipscombe. The rain-powered cart. Eur. J. Phys. 37 (2016) 055005
Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

