Un proyectil de masa m y velocidad u, choca contra un bloque de longitud L y de masa M inicialmente en reposo. El bloque está provisto de un muelle elástico de constante k, contra el que impacta el proyectil. El conjunto se mueve sobre un plano horizontal sin rozamiento

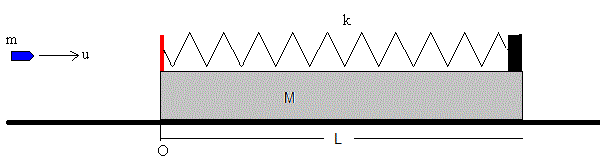
Después del choque, el muelle se comprime x_m y el proyectil junto con el bloque se mueven con la misma velocidad v , tal como se muestra en la figura

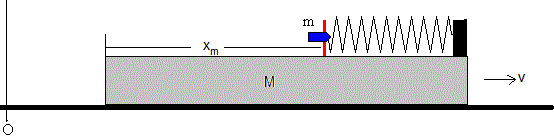
Aplicamos el principio de conservación del momento lineal al sistema aislado formado por el proyectil y el bloque.

mu=(m+M)v

La energía cinética del proyectil se transforma en energía cinética de los dos cuerpos y en energía potencial del muelle elástico deformado.

${\displaystyle \frac{1}{2}m{u}^2=\frac{1}{2}(m+M)v^2+\frac{1}{2}k{x}_m^2}$

Despejamos la máxima deformación del muelle x_m

${\displaystyle x_m=u\sqrt{\frac{1}{k}\frac{mM}{m+M}}}$

Movimiento de los dos cuerpos

En el apartado anterior, comparamos las situación inicial y la situación final después del choque. En este apartado, examinamos el movimiento del proyectil y del bloque mientras se va deformando el muelle elástico como resultado del impacto del proyectil.

Examinamos:

• El movimiento del centro de masas con velocidad constante
• El movimiento relativo de los dos cuerpos bajo la acción de la fuerza que ejerce el muelle deformado

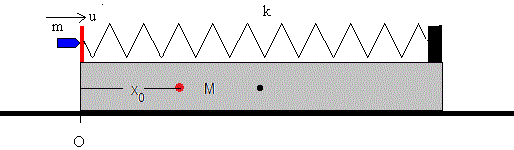
En el instante inicial t=0, la posición del proyectil es x₁=0 y su velocidad es v₁=u, la posición del extremo del bloque es x₂=0 y su velocidad v₂=0. El muelle no ha deformado todavía, x=0

La posición del centro de masas del sistema (punto de color rojo) formado por el proyectil, considerado una masa puntual y el bloque es

${\displaystyle X_0=\frac{m{x}_1+M\left(x_2+L/2\right)}{m+M}=\frac{M\left(L/2\right)}{m+M}}$

El centro de masas del bloque de longitud L, se encuentra en L/2 (punto de color negro)

La velocidad del centro de masas del sistema aislado formado por el proyectil y el bloque es constante, lo que equivale a decir que se conserva el momento lineal.

${\displaystyle V=\frac{m{v}_1+M{v}_2}{m+M}=\frac{mu}{m+M}}$

La energía inicial es la cinética del proyectil

${\displaystyle E=\frac{1}{2}m{u}^2}$

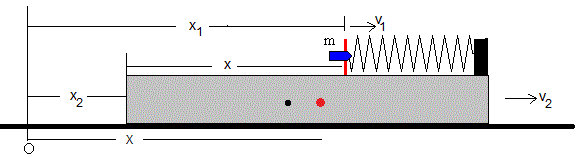
En el instante t, el muelle se ha deformado x, la velocidad del proyectil se ha reducido de u a v₁ y la velocidad del bloque ha aumentado de cero a v₂.

La posición del proyectil es x₁ y la posición del extremo del bloque es x₂. Como vemos en la figura x₁-x₂=x.

La energía inicial se convierte en energía cinética de los dos cuerpos y en energía potencial del muelle deformado x

${\displaystyle \frac{1}{2}m{u}^2=\frac{1}{2}m{v}_1^2+\frac{1}{2}M{v}_2^2+\frac{1}{2}k{x}^2}$

Movimiento del centro de masas

La posición del centro de masas en el instante t, es

${\displaystyle X=\frac{m{x}_1+M\left(x_2+L/2\right)}{m+M}}$

Como el centro de masas se mueve con velocidad V constante

${\displaystyle \begin{array}{l}V=\frac{m{v}_1+M{v}_2}{m+M}=\frac{mu}{m+M}\\ m{v}_1+M{v}_2=mu\end{array}}$

La posición del centro de masas en el instante t, es X=X₀+Vt

${\displaystyle \begin{array}{l}\frac{m{x}_1+M\left(x_2+L/2\right)}{m+M}=\frac{M\left(L/2\right)}{m+M}+\frac{mu}{m+M}t\\ m{x}_1+M{x}_2=mut\end{array}}$

Movimiento del proyectil y el bloque

Sobre el proyectil actúa la fuerza que ejerce el muelle comprimido x, -kx. La ecuación del movimiento del proyectil es

${\displaystyle m\frac{d^2{x}_1}{d{t}^2}=-kx}$

Sobre el bloque actúa la misma fuerza en sentido contrario, kx. La ecuación del movimiento del bloque es

${\displaystyle M\frac{d^2{x}_2}{d{t}^2}=kx}$

Se combinan ambas en una única ecuación difrencial

${\displaystyle \begin{array}{l}\frac{d^2\left(x_1-x_2\right)}{d{t}^2}=-\left(\frac{1}{m}+\frac{1}{M}\right)kx\\ \frac{d^{2}x}{d{t}^2}=-\left(\frac{1}{m}+\frac{1}{M}\right)kx\end{array}}$

La solución de esta ecuación diferencial es

${\displaystyle \begin{array}{l}x=A\sin \left(\omega t\right)+B\cos \left(\omega t\right){\omega }^2=k\frac{m+M}{mM}\\ \frac{dx}{dt}=\omega \left(A\cos \left(\omega t\right)-B\sin \left(\omega t\right)\right)\end{array}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales en el instante t=0: x₁=0, x₂=0, dx₁/dt=u, dx₂/dt=0. Como x=x₁-x₂, en el instante t=0, x=0, y dx/dt=u. La solución de la ecuación diferencial en x es

${\displaystyle x=\frac{u}{\omega }\sin \left(\omega t\right)}$

Conocido x, calculamos las posiciones del proyectil, x₁ y del extremo del bloque x₂, a partir de las relaciones

${\displaystyle \begin{array}{l}{x}_1-x_2=\frac{u}{\omega }\sin \left(\omega t\right)\\ m{x}_1+M{x}_2=mut\end{array}}$

Despejamos x₁ y x₂ en el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{x}_1=\frac{mu}{m+M}\left(t+\frac{M}{m\omega }\sin \left(\omega t\right)\right)\\ x_2=\frac{mu}{m+M}\left(t-\frac{1}{\omega }\sin \left(\omega t\right)\right)\end{array}}$

Las velocidades del proyectil y del bloque son, respectivamente

${\displaystyle \begin{array}{l}{v}_1=\frac{d{x}_1}{dt}=\frac{mu}{m+M}\left(1+\frac{M}{m}\cos \left(\omega t\right)\right)\\ v_2=\frac{d{x}_2}{dt}=\frac{mu}{m+M}\left(1-\cos \left(\omega t\right)\right)\end{array}}$

Ambas velocidades se hacen iguales en el instante t_c tal que cos(ωt_c)=0, t_c=π/(2ω). En este instante la velocidad final del proyectil y del bloque es

v₁=v₂=v=mu/(m+M)

m=0.4; % masa de la bala
M=1; %masa del bloque
u=10; %velocidad de la bala
k=50; %constante del muelle 

%tiempo que tardan en alcanzar la misma velocidad
w=sqrt(k*(m+M)/(m*M));
tc=pi/(2*w);  
t=0:0.005:2*tc;
v1=(m*u*(1+M*cos(w*t)/m)/(m+M)).*(t<tc)+(m*u/(m+M))*(t>=tc);
v2=(m*u*(1-M*cos(w*t))/(m+M)).*(t<tc)+(m*u/(m+M))*(t>=tc);

hold on
plot(t,v1)
plot(t,v2)
hold off
legend('bala','bloque')
xlabel('t(s)')
ylabel('v(m)')
title('Choque entre una bala y un bloque')
grid on

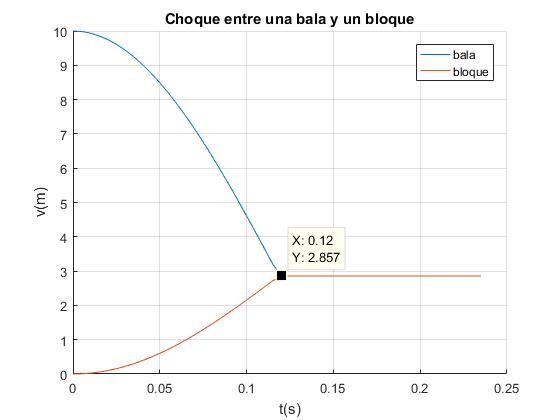
En el instnate t_c=0.1187 s las velocidades del proyectil y del bloque se hacen iguales, v=mu/(m+M).

>> tc
tc =    0.1187
>> m*u/(m+M)
ans =    2.8571

Energías

A partir de las expresiones de x₁, x₂, v₁ y v₂ en función del tiempo, comprobamos que se cumple

• el principio de conservación del momento lineal

mv₁+Mv₂=mu

• el principio de conservación de la energía

${\displaystyle \frac{1}{2}m{v}_1^2+\frac{1}{2}M{v}_2^2+\frac{1}{2}k{x}^2=\frac{1}{2}m{u}^2}$

Cuando las velocidades del proyectil y del bloque son iguales, v=mu/(M+m), la energía almacenada en el muelle elástico es

${\displaystyle \frac{1}{2}k{x}_m^2=\frac{1}{2}\frac{mM}{m+M}{u}^2}$

que es la energía perdida en un choque inelástico entre una bala de masa m que lleva una velocidad u y un bloque de masa M inicialmente en reposo

Actividades

Se introduce

• La masa m de la bala en kg, en el control titulado Masa bala
• La velocidad u de la bala en m/s, en el control titulado Velocidad bala
• La constante k en N/m del muelle elástico, en el control titulado Constante.
• La masa del bloque está fijada en el valor M=1 kg
• La longitud del bloque se ha fijado en el valor L=1 m

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la bala, cómo va deformando el muelle a la vez que disminuye su velocidad y aumenta la del bloque.

En la parte izquierda observamos los cambios energéticos:

• La energía cinética del bloque en color rojo
• La energía cinética de la bala en color azul
• La energía potencial elástica del muelle en coor gris.

Ejemplo:

• masa del bloque, M=1 kg
• masa de la bala, m=0.4 kg
• velocidad de la bala, u=10 m/s
• Constante del muelle, k=50 N/m

La bala y el bloque alcanzan la misma velocidad v=mu/(m+M)=2.86 m/s, en el instante t_c=π/(2ω)=0.12 s. El desplazamiento de la bala y el bloque en este instante son

${\displaystyle \begin{array}{l}{x}_1=\frac{mu}{m+M}\left(t_c+\frac{M}{m\omega }\right)\\ x_2=\frac{mu}{m+M}\left(t_c-\frac{1}{\omega }\right)\end{array}}$

x₁=0.88 m, x₂=0.12 m