Transferencia de energía cinética en una secuencia de colisiones

Choque de dos partículas

Consideremos el choque de dos partículas de masas m y M, la segunda está en reposo antes del choque. La conservación del momento lineal es

mu=mv+MV

De la definición del coeficiente de restitución

-e(u-0)=v-V

Despejando las velocidades después del choque v y V

$v = \frac{m - M e}{m + M} u, V = \frac{m (1 + e)}{m + M} u$

La energía cinética final de la segunda partícula es

$E_{M}^{f} = \frac{1}{2} M V^{2} = \frac{1}{2} M {(\frac{m (1 + e)}{m + M})}^{2} u^{2} = \frac{{(1 + e)}^{2} m M}{{(m + M)}^{2}} (\frac{1}{2} m u^{2})$

La proporción η de la energía cinética de la primera partícula que se transfierea a la segunda es

$η = \frac{E_{M}^{f}}{E_{m}^{i}} = \frac{\frac{1}{2} M V^{2}}{\frac{1}{2} m u^{2}} = \frac{{(1 + e)}^{2} m M}{{(m + M)}^{2}} = \frac{{(1 + e)}^{2} x}{{(x + 1)}^{2}}, x = \frac{m}{M}$

Calculamos el máximo de la función η(x) del siguiente modo. η(x) es proporcional a y=x/(x+1)². Calculamos la derivada primera de la función y=f(x), ayudándonos de Math Symbolic

>> syms x;
>> y=x/(1+x)^2;
>> z=diff(y);
>> simplify(z)
 ans =- (x - 1)/(x + 1)^3

$\frac{d y}{d x} = \frac{1 - x}{{(1 + x)}^{2}}$

La derivada primera, se hace cero para x=1, es decir, m=M, las masas de las dos partícula son iguales. Calculamos la derivada segunda

>> zz=diff(z)
>> simplify(zz)
 ans =(2*(x - 2))/(x + 1)^4
>> subs(zz,x,1)
 ans =-1/8

$\frac{d^{2} y}{d x^{2}} = 2 \frac{x - 2}{{(1 + x)}^{4}}$

La derivada segunda de y=f(x) es negativa para x=1, indicando un máximo.

La máxima transferencia de energía cinética en este choque ocurre cuando las masas de las partículas son iguales m=M, lo mismo que en un choque elástico entre dos partículas, cuando la segunda está en reposo antes del choque.

Las velocidades de las partículas después del choque, cuando m=M, y la proporción η_m de energía que se transfiere

$\begin{array}{l} v = \frac{1 - e}{2} u, V = \frac{1 + e}{2} u \\ η_{m} = \frac{{(1 + e)}^{2}}{4} \end{array}$

Cuando la colisión es elástica, e=1, v=0, V=u y η_m=1, se transfiere toda la energía

Una partícula mediadora

Situamos una partícula mediadora de masa m₁, entre las dos partículas de masa m y M. La velocidad inicial de la partícula de masa m es u, las otras dos están en reposo

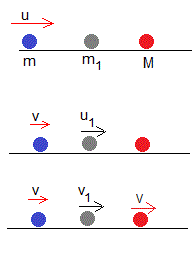
Choque entre la primera partícula de masa m y velocidad inicial u con la intermedia, de masa m₁ en reposo. Las velocidades después del choque v y u₁, son

$v = \frac{m - m_{1} e_{1}}{m + m_{1}} u, u_{1} = \frac{m (1 + e_{1})}{m + m_{1}} u$

Siendo, e₁ el coeficiente de restitución del primer choque

Choque de la partícula intermedia de masa m₁ y velocidad u₁, con la partícula de masa M en reposo. Las velocidades después del choque v₁ y V, son

$v_{1} = \frac{m_{1} - M e_{2}}{m_{1} + M} u_{1} V = \frac{m_{1} (1 + e_{2})}{m_{1} + M} u_{1} = \frac{m (1 + e_{1})}{m + m_{1}} \frac{m_{1} (1 + e_{2})}{m_{1} + M} u$

Siendo, e₂ el coeficiente de restitución del segundo choque

La proporción η de la energía cinética de la primera partícula m transferida a la segunda M a través de la partícula intermedia m₁ es

$η = \frac{\frac{1}{2} M V^{2}}{\frac{1}{2} m u^{2}} = m M \frac{{(1 + e_{1})}^{2} {(1 + e_{2})}^{2} m_{1}^{2}}{{(m + m_{1})}^{2} {(m_{1} + M)}^{2}}$

La masa de la partícula intermedia m₁ para que la poroporción η sea máxima, se calcula del siguiente modo:

Denominamos x=m₁, la función η(x) es porporcional a y=x²/((m+x)²(x+M)²). Calculamos la derivada primera de la función y=f(x), ayudándonos de Math Symbolic de MATLAB

>> syms x m M;
>> y=x^2/((m+x)^2*(x+M)^2);
>> z=diff(y,x);
>> simplify(z)
 ans =(2*x*(- x^2 + M*m))/((M + x)^3*(m + x)^3)

$\frac{d y}{d m_{1}} = \frac{2 m_{1} (M m - m_{1}^{2})}{{(m + m_{1})}^{3} {(m_{1} + M)}^{3}}$

El máximo se obtiene para $m_{1}^{2} = m M$

Calculamos la derivada segunda

>> zz=diff(z,x);
>> simplify(zz)
ans =-(2*(- M^2*m^2 + 2*M^2*m*x + 2*M*m^2*x + 8*M*m*x^2 - 3*x^4))/
((M + x)^4*(m + x)^4)

$- \frac{2 (- m^{2} M^{2} + 2 m^{2} M m_{1} + 2 m M^{2} m_{1} + 8 m M m_{1}^{2} - 3 m_{1}^{4})}{{(m + m_{1})}^{4} {(m_{1} + M)}^{4}}$

Cuando $m_{1}^{2} = m M$ , la suma del primer término, cuarto y quinto del numerador

$- m^{2} M^{2} + 8 m M m_{1}^{2} - 3 m_{1}^{4} = - m^{2} M^{2} + 8 m^{2} M^{2} - 3 m^{2} M^{2} = 4 m^{2} M^{2}$

La derivada segunda es negativa para dicho valor de la masa intermedia m₁, y por tanto, η(m₁) es máximo

$η_{m} = {(\frac{(1 + e_{1}) (1 + e_{2}) m M}{(m + \sqrt{m M}) (\sqrt{m M} + M)})}^{2} = \frac{{(1 + e_{1})}^{2} {(1 + e_{2})}^{2} m M}{{(\sqrt{m} + \sqrt{M})}^{4}}$

Las velocidades finales de las tres partículas son

$\begin{array}{l} v = \frac{m - m_{1} e_{1}}{m + m_{1}} u, v_{1} = \frac{m_{1} - M e_{2}}{m_{1} + M} \frac{m (1 + e_{1})}{m + m_{1}} u, V = \frac{m (1 + e_{1})}{m + m_{1}} \frac{m_{1} (1 + e_{2})}{m_{1} + M} u \\ v = \frac{\sqrt{m} - \sqrt{M} e_{1}}{\sqrt{m} + \sqrt{M}} u, v_{1} = \sqrt{m} (1 + e_{1}) \frac{\sqrt{m} - \sqrt{M} e_{2}}{{(\sqrt{m} + \sqrt{M})}^{2}} u, V = \frac{m (1 + e_{1}) (1 + e_{2})}{{(\sqrt{m} + \sqrt{M})}^{2}} u \end{array}$

Choques elásticos

Si las colisiones son elásticas, e₁=e₂=1

$η_{m} = \frac{16 m M}{{(\sqrt{m} + M)}^{4}}$

Actividades.

La masa de la tercera partícula se ha fijado en el valor M=1 kg.
La velocidad inicial de la primera partícula se ha fijado en u=1 m/s

Se introduce

La masa m de la primera partícula, en el control titulado Masa primera.
La masa de la partícula mediadora m₁, en el control titulado Masa mediadora.

Se pulsa el botón titulado Nuevo

Observamos, el choque entre la primera partícula y la segunda. A continuación, el choque entre la segunda y la tercera. No se consideran otros posibles choques entre las partículas.

En la parte superior, aparecen los datos de las velocidades de las partículas antes y después de los choques. Comprobamos que la velocidad V de la tercera partícula después del segundo choque es

$V = \frac{4 m m_{1}}{(m + m_{1}) (m_{1} + M)} u$

Fijada la masa m de la primera partícula, vamos cambiando la masa m₁ de la partícula intermedia hasta conseguir que la energía cinética de la tercera partícula después del segundo choque sea máxima. Comprobaremos, que se cumple la condición de extremo, $m_{1} = \sqrt{m M}$

Ejemplo 1

Sean las masas de las partículas

m=25 kg
M=1 kg

Completamos una tabla de valores como la siguiente:

m₁ (kg)	V (m/s)
4	2.759
5	2.778
6	2.765

La velocidad máxima V de la tercera partícula se obtiene para el valor m₁=5, tal como comprobamos a partir de la condición de extremo $m_{1} = \sqrt{25 \cdot 1} = 5$

Ejemplo 2:

Sean las masas de las partículas

m=10000 kg
m₁=100 kg
M=1 kg

La masa de la segunda partícula m₁ es tal que se cumple la condición de máximo de V, pero como m es muy grande comparado con M, la velocidad V es muy cercana al valor de 4, que es la más alta velocidad que puede alcanzar la tercera partícula.

$\begin{array}{l} V = \frac{4 m}{{(\sqrt{m} + \sqrt{M})}^{2}} u = \frac{4}{{(1 + \sqrt{\frac{M}{m}})}^{2}} u \\ \lim_{x \to 0} \frac{4}{{(1 + \sqrt{x})}^{2}} u = 4 u \end{array}$

Balance energético

La energía inicial de la primera partícula es, $E_{1} = \frac{1}{2} m u^{2}$

Después del primer choque entre la primera y segunda partícula, la energía se reparte ente la primera F₁ y segunda partícula E₂, de modo que E₁=F₁+E₂

Después del segundo choque entre la segunda y tercera partícula, la energía cinética E₂ de la segunda partícula se reparte entre la segunda F₂ y tercera partícula E₃, de modo que E₂=F₂+E₃

Al finalizar el segundo choque, se cumplirá que E₁=F₁+ F₂+ E₃, siendo E₁ la energía inicial de la primera partícula y F₁, F₂, E₃ las energía finales de las tres partículas.

Ejemplo 3:

En la parte superior, aparece una barra horizontal dividida en dos porciones después del primer choque o en tres porciones después del segundo choque. Cada porción representa la energía cinética de las tres partículas.

Sean las masas de las partículas

m=25 kg
m₁=5 kg
M=1 kg

La velocidad inicial de la primera partícula es u=1.0, su energía cinética inicial es E₁=12.5 J

Después del primer choque

La primera partícula lleva una velocidad de v=0.667 m/s, su energía cinética es F₁=5.556 J

La partícula intermedia lleva una velocidad u₁=1.667 m/s, su energía cinética es E₂=6.944 J

La suma de ambas energías es la energía cinética inicial E₁=F₁+E₂

Después del segundo choque

La partícula intermedia lleva una velocidad v₁=1.111 m/s, su energía cinética es F₂=3.086 J

La tercera partícula lleva una velocidad V=2.778 m/s, su energía cinética es E₃=3.858 J

Comprobamos que E₂=F₂+E₃, y también E₁=F₁+ F₂+E₃

Masa primera m
Masa mediadora m₁

Dos partículas mediadoras

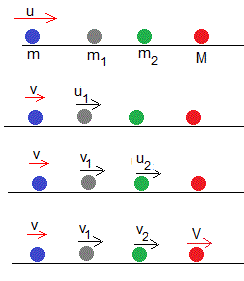
Situamos dos partículas mediadoras de masa m₁ y m₂, entre las dos partículas de masa m y M. La velocidad inicial de la partícula de masa m es u, las otras tres están inicialmente en reposo

Choque entre la primera partícula de masa m y velocidad inicial u con la intermedia, de masa m₁ en reposo. Las velocidades después del choque v y u₁, son

$v = \frac{m - m_{1} e_{1}}{m + m_{1}} u u_{1} = \frac{m (1 + e_{1})}{m + m_{1}} u$

Siendo, e₁ el coeficiente de restitución del primer choque

Choque de la partícula intermedia de masa m₁ y velocidad u₁, con la partícula intermedia de masa m₂ en reposo. Las velocidades después del choque v₁ y u₂, son

$v_{1} = \frac{m_{1} - m_{2} e_{2}}{m_{1} + m_{2}} u_{1} u_{2} = \frac{m_{1} (1 + e_{2})}{m_{1} + m_{2}} u_{1} = \frac{m (1 + e_{1})}{m + m_{1}} \frac{m_{1} (1 + e_{2})}{m_{1} + m_{2}} u$

Siendo, e₂ el coeficiente de restitución del segundo choque

Choque de la partícula intermedia de masa m₂ y velocidad u₂, con la partícula de masa M en reposo. Las velocidades después del choque v₂ y V, son

$v_{2} = \frac{m_{2} - M e_{3}}{m_{2} + M} u_{2} V = \frac{m_{2} (1 + e_{3})}{m_{2} + M} u_{2} = \frac{m (1 + e_{1})}{m + m_{1}} \frac{m_{1} (1 + e_{2})}{m_{1} + m_{2}} \frac{m_{2} (1 + e_{3})}{m_{2} + M} u$

La proporción η de la energía cinética de la primera partícula transferida a la segunda a través de las dos partículas mediadoras es

$η = \frac{\frac{1}{2} M V^{2}}{\frac{1}{2} m u^{2}} = m M {(\frac{m_{1} m_{2} (1 + e_{1}) (1 + e_{2}) (1 + e_{3})}{(m + m_{1}) (m_{1} + m_{2}) (m_{2} + M)})}^{2}$

Para calcular el máximo de la función η(m₁, m₂) utilizando Math Symbolic de MATLAB, denominamos x=m₁ e y=m₂, la función η(x, y) es porporcional a

$z = f (x, y) = {(\frac{x y}{(m + x) (x + y) (y + M)})}^{2}$

Calculamos las derivadas parciales de z respecto de x e y

>> syms x y m M;
>> z=(x*y/((m+x)*(x+y)*(y+M)))^2;
>> zx=diff(z,x);
>> simplify(zx)
ans =(2*x*y^2*(- x^2 + m*y))/((M + y)^2*(m + x)^3*(x + y)^3)
>> zy=diff(z,y);
>> simplify(zy)
ans =(2*x^2*y*(- y^2 + M*x))/((M + y)^3*(m + x)^2*(x + y)^3)

$\begin{array}{l} \frac{\partial y}{\partial m_{1}} = \frac{2 m_{1} m_{2}^{2} (m m_{2} - m_{1}^{2})}{{(m + m_{1})}^{3} {(m_{1} + m_{2})}^{3} {(m_{2} + M)}^{2}} = 0 \\ \frac{\partial y}{\partial m_{2}} = \frac{2 m_{1}^{2} m_{2} (M m_{1} - m_{2}^{2})}{{(m + m_{1})}^{2} {(m_{1} + m_{2})}^{3} {(m_{2} + M)}^{3}} = 0 \end{array}$

Obtenemos un sistema de dos ecuaciones

${\begin{cases} m_{1}^{2} = m m_{2} \\ m_{2}^{2} = M m_{1} \end{cases}$

De la que se deduce la relaciones

$\begin{array}{l} m_{1} m_{2} = m M \\ \frac{m_{1}}{m_{2}} = {(\frac{m}{M})}^{1 / 3} \\ \frac{m}{m_{1}} = \frac{m_{1}}{m_{2}} = \frac{m_{2}}{M} = r, {\begin{cases} m_{1} = m r^{- 1} \\ m_{2} = m r^{- 2} \end{cases} \end{array}$

La proporción η_m máxima es

$η_{m} = m M \frac{{(1 + e_{1})}^{2} {(1 + e_{2})}^{2} {(1 + e_{3})}^{2}}{{(m^{1 / 3} + M^{1 / 3})}^{6}}$

Las velocidades finales de las cuatro partículas son

$\begin{array}{l} v = \frac{r - e_{1}}{r + 1} u \\ v_{1} = \frac{r - e_{2}}{r + 1} \frac{r (1 + e_{1})}{r + 1} u = \frac{r (1 + e_{1}) (r - e_{2})}{{(r + 1)}^{2}} u \\ v_{2} = \frac{r - e_{3}}{r + 1} \frac{r (1 + e_{1})}{r + 1} \frac{r (1 + e_{2})}{r + 1} u = \frac{r^{2} (1 + e_{1}) (1 + e_{2}) (r - e_{3})}{{(r + 1)}^{3}} \\ V = \frac{m (1 + e_{1})}{m + m_{1}} \frac{m_{1} (1 + e_{2})}{m_{1} + m_{2}} \frac{m_{2} (1 + e_{3})}{m_{2} + M} u = \frac{r^{3} (1 + e_{1}) (1 + e_{2}) (1 + e_{3})}{{(r + 1)}^{3}} u \end{array}$

Si las colisiones son elásticas, e₁=e₂=e₃=1

$η_{m} = \frac{64 m M}{{(m^{1 / 3} + M^{1 / 3})}^{6}}$

n partículas mediadoras

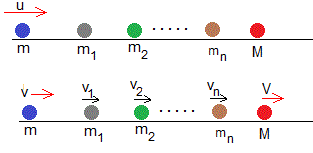
Generalizamos, los resultados obtenidos para dos partículas mediadoras a n partículas mediadoras

La proporción de la energía cinética de la primera partícula transferida a la última a través de n partículas mediadoras es

$η = \frac{\frac{1}{2} M V^{2}}{\frac{1}{2} m u^{2}} = m M {(\frac{m_{1} m_{2} .... m_{n} (1 + e_{1}) (1 + e_{2}) .... (1 + e_{n}) (1 + e_{n + 1})}{(m + m_{1}) (m_{1} + m_{2}) .... (m_{n - 1} + m_{n}) (m_{n} + M)})}^{2}$

Calculamos el máximo de la función η(m₁, m₂...m_n)

$\begin{array}{l} z = f (m_{1}, m_{2},... m_{n}) = {(\frac{m_{1} m_{2} .... m_{n}}{(m + m_{1}) (m_{1} + m_{2}) .... (m_{n - 1} + m_{n}) (m_{n} + M)})}^{2} \\ \frac{\partial z}{\partial m_{k}} = 0, k = 1,2,3... n \end{array}$

La masas de las partículas forman una progresión geométrica de razón r

$\begin{array}{l} \frac{m}{m_{1}} = \frac{m_{1}}{m_{2}} = \frac{m_{2}}{m_{3}} = ... = \frac{m_{n - 1}}{m_{n}} = \frac{m_{n}}{M} = r, {\begin{cases} m_{1} = m r^{- 1} \\ m_{2} = m r^{- 2} \\ .... \\ m_{n} = m r^{- n} \end{cases} \\ r = {(\frac{m}{M})}^{1 / (n + 1)} \end{array}$

Las velocidades finales cuando los coeficientes de restitución son iguales, e₁=e₂=....=e_n+1

$\begin{array}{l} v = \frac{r - e}{r + 1} u \\ v_{k} = \frac{r^{k} {(1 + e)}^{k} (r - e)}{{(r + 1)}^{k + 1}}, k = 1,2,... n \\ V = \frac{r^{n + 1} {(1 + e)}^{n + 1}}{{(r + 1)}^{n + 1}} u \end{array}$

Cuando los coeficientes de restitución de todos los choques son iguales, la proporción η_m máxima es

$η_{m} = m M \frac{{(1 + e)}^{2 (n + 1)}}{{(m^{1 / (n + 1)} + M^{1 / (n + 1)})}^{2 (n + 1)}}$

Representamos η_m en función del número de choques n, para x=M/m=0.2 y para tres valores del coeficiente de restitución e=0.80, 0.90 y 0.95

$η_{m} = x {(\frac{1 + e}{1 + x^{1 / n + 1}})}^{2 (n + 1)}$

x=0.2; %M/m
colores=['r','b','k'];
i=1;
hold on
for e=[0.80,0.90,0.95] %coeficiente de restitución
    f=@(n) x*((1+e)/(1+x^(1/(n+1))))^(2*(n+1));
    for n=0:10
       plot(n,f(n),'o','markersize',3,'markeredgecolor',colores(i),
'markerfacecolor',colores(i))
    end
    i=i+1;
end
hold off
grid on
xlabel('n')
ylabel('\eta_m')
title('Transferencia de energía')

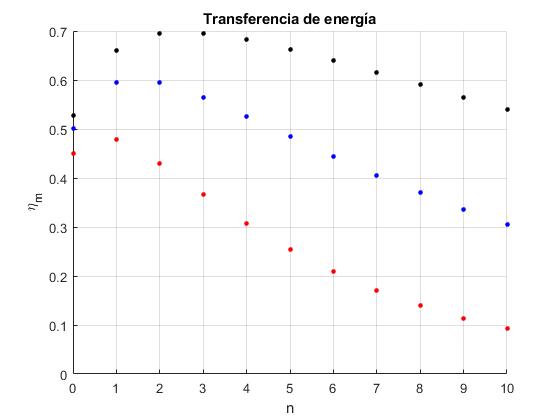
Vemos que para e=0.8 (color rojo), el máximo de η_m se obtiene para n=1, partículas mediadoras. Para e=0.95 (color negro) el máximo de η_m se obtiene para n=2 ó 3, partículas mediadoras

Derivamos la expresión de η_m con respecto de n e igualamos a cero. para ello, utilizamos la regla de derivación de la función

$\begin{array}{l} y = u {(x)}^{v (x)} \\ \ln y = v (x) \ln u (x) \\ \frac{y'}{y} = v' (x) \ln u (x) + v (x) \frac{u' (x)}{u (x)} \\ y' = u {(x)}^{v (x)} (v' (x) \ln u (x) + v (x) \frac{u' (x)}{u (x)}) \end{array}$

El resultado es

$\begin{array}{l} \frac{\partial η_{m}}{\partial n} = 0 \\ \ln (1 + e) - \ln (x^{1 / n + 1} + 1) + \frac{1}{n + 1} \frac{x^{1 / n + 1} \ln x}{x^{1 / n + 1} + 1} = 0 \end{array}$

Dado x=M/m y e, resolvemos la ecuación transcendente utilizando la función fzero de MATLAB

x=0.2;
e=0.95;
f=@(n) x*((1+e)/(1+x^(1/(n+1))))^(2*(n+1));

g=@(n) log(1+e)-log(x^(1/(1+n))+1)+x^(1/(1+n))*log(x)/((n+1)*(x^(1/(1+n))+1));
n=fzero(g,1);
disp([round(n)])

El entero más próximo es

    3
>> f(3)
ans =    0.6953

Bastan tres partículas mediadoras para obtener la máxima proporción de transferencia de energía desde la partícula incidente m a la última de masa M, fijada la relación entre masas x=M/m=0.2 y el coeficiente de restitución común para todas las colisiones, e=0.95.

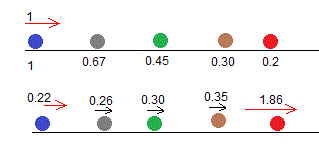
Suponiendo que la masa de la primera partícula m=1, la última M=x·m=0.2, las masas de las partículas mediadoras son: m₁=m/r, m₂=m/r², m₃=m/r³, M=m/r⁴. De esta última, se obtiene r=1.4953,

Las masas de las partículas son: m=1, m₁=0.6687, m₂=0.4472, m₃=0.2991, M=0.2

Las velocidades de las partículas después de los sucesivos choques son: v=0.2185, v₁=0.2554, v₂=0.2984, v₃=0.3487, V=1.8646

El número de masas mediadoras se reduce al disminuir el coeficiente de restitución e y aumentar x=M/m. Al disminuir el número de masas mediadoras aumenta la proporción η_m, de la energía cinética inicial de la partícula de masa m transferida a la última partícula de masa M. Por ejemplo, para e=0.95 y x=0.1, 0.3, 0.5, 0.7, 0.9, obtenemos los siguientes resultados

e=0.95;
disp(['n','    %E_k'])
for x=0.1:0.2:0.9
    f=@(n) x*((1+e)/(1+x^(1/(n+1))))^(2*(n+1));
    g=@(n) log(1+e)-log(x^(1/(1+n))+1)+x^(1/(1+n))*log(x)/((n+1)*(x^(1/(1+n))+1));
    n=round(fzero(g,1));
    if n<0
        n=0;
    end
    fprintf('%i,   %1.4f\n',n,f(n))
end

n    %E_k
4,   0.5969
2,   0.7619
1,   0.8513
0,   0.9210
0,   0.9480

Referencias

Bernard Ricardo, Paul Lee. Maximizing kinetic energy transfer in onedimensional many-body collisions. Eur. J. Phys. 36(2015) 025013

Renu Raman Sahu. On the optimization of dissipative chain events. Am. J. Phys. 88(2), February 2020, pp. 124-127

Fakhruddin H. Maximizing imparted speed in elastic collisions. The Physics Teacher, Vol 41, September 2003, pp. 338-33