Demostración de la conservación del momento lineal
Simulación de la cuna de Newton. Pulse el boton titulado ►
Cadena de n-bolas en contacto
En este apartado, vamos a describir las ecuaciones del movimiento del centro de masas (c.m.) de cada una de las bolas, que forman parte de una cadena de n bolas elásticas en contacto.
Consideremos las fuerzas entre dos partículas unida por un muelle elástico.
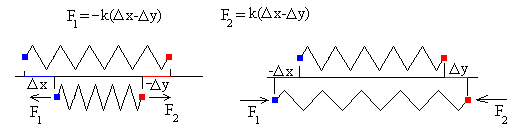
En la parte superior se muestra el muelle sin deformar y en la parte inferior, el muelle deformado. Las deformaciones del muelles son Δx=x-x0, donde x es la posición de la primera partícula (azul) cuando el muelle se ha deformado, y x0 es la posición de dicha partícula cuando el muelle está sin deformar. Lo mismo cabe decir de Δy. Las fuerza de interacción es el producto de la constante k del muelle por la deformación del muelle o diferencia entre la longitud sin deformar y la longitud del muelle deformado k(|Δx|+|Δy|) .
Consideremos un conjunto de cinco partículas unidas por muelles elásticos, en un instante inicial en el que los muelles están sin deformar (arriba), y en un instante tal (abajo) en el que la primera partícula se ha desplazado x1, la segunda x2, la tercera x3, la cuarta x4 y la quinta x5. Las fuerzas sobre cada una de las partículas se indican en la figura, y se señalan los pares de fuerzas: la primera partícula ejerce una fuerza sobre la segunda y la segunda ejerce una fuerza igual y de sentido contrario sobre la primera.
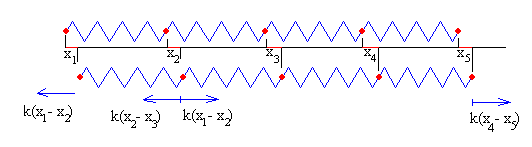
Supongamos que los muelles no son lineales, y su comportamiento está de acuerdo a una ley de fuerza cuyo exponente es r=3/2. Las ecuaciones del movimiento de cada una de las partículas son
Sumando miembro a miembro, comprobamos que la aceleración del centro de masas es cero, como corresponde a un sistema aislado formado por cinco partículas interactuantes.
El ejemplo de una cadena de cinco bolas se puede generalizar a una cadena de n bolas.
Tenemos un sistema de n ecuaciones diferenciales acopladas que se resuelve por procedimientos numéricos con las siguientes condiciones iniciales
En el instante t=0,
-
Todas las partículas están en sus posiciones de equilibrio. xi=0, i=1...n
-
Todas las partículas están en reposo, excepto la partícula incidente que lleva velocidad v en el instante t=0 en el que choca con la segunda partícula. v1=v, vi=0, i=2…n
Simulación
La simulación del comportamiento de la cadena de n-bolas idénticas se ha dividido en tres partes:
-
Se desplaza la primera bola de la posición de equilibrio y se suelta. Si el c.m. de la bola asciende una altura h, la velocidad v de la primera bola en el momento en el que choca con la segunda bola en reposo es
-
Una vez que la bola incidente entra en contacto con la segunda bola, se resuelve el sistema de ecuaciones diferenciales acopladas, para determinar el desplazamiento de cada una de las bolas y las velocidades de las mismas.
-
La velocidad del c.m. en (m/s) de cada una de las bolas en función del tiempo. La velocidad de la primera bola disminuye y tiende hacia un valor próximo a cero, la velocidad de la segunda bola aumenta y luego disminuye, la velocidad de la última bola aumenta hasta un valor próximo a la velocidad de la bola incidente.
-
La resultante de las fuerzas en 103 N sobre cada una de las bolas
-
El desplazamiento xi en 10-5 m de del c.m. de cada una de las bolas en función del tiempo.
-
La última bola alcanza una velocidad vn en el momento en el que se separa de la penúltima bola n-1. Como ocurre con un péndulo su energía cinética se convierte en energía potencial cuando alcanza el máximo desplazamiento angular
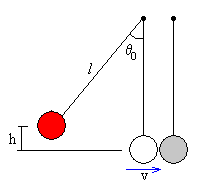
La bola incidente que cuelga de un hilo de longitud l se comporta como un péndulo, describiendo un MAS de amplitud θ0, tal que h=l-l·cosθ0
La ecuación del MAS es θ= -θ0cos(ωt), con
La primera bola choca con la segunda cuando ωt=π/2.
Se representa, en el eje horizontal, el tiempo en 10-4 s, y en el eje vertical
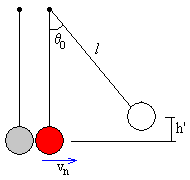
La bola final que cuelga de un hilo de longitud l se comporta como un péndulo, describiendo un MAS de amplitud θ0, tal que
h’=l-l·cosθ0
La ecuación del MAS es θ=θ0sin(ωt)
Propagación de la perturbación
El tiempo de propagación tp de la perturbación a lo largo de la cadena se define como el intervalo de tiempo que trascurre desde el contacto entre la primera y la segunda bola (t=0), y el instante de separación de las dos últimas bolas tp, es decir, el instante de la intersección del desplazamiento de la penúltima bola xn-1 y de la última bola xn, tal como se ve en la figura.
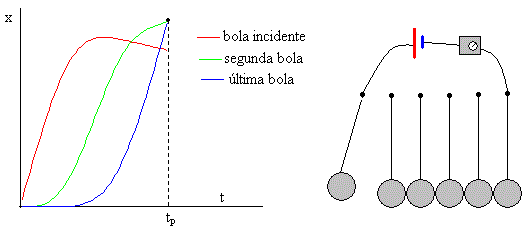
En el laboratorio, el tiempo de propagación se puede medir del siguiente modo: se pone en marcha un reloj electrónico cuando se cierra el circuito, en el momento en el que la primera y la segunda bola entran en contacto. El reloj se para, cuando se interrumpe el paso de la corriente eléctrica entre la penúltima y última bola, en el momento en el que dejan de estar en contacto.
Actividades
Se introduce
-
El número de bolas, en el control titulado Número de bolas
Se pulsa el botón titulado Nuevo
Observamos las tres etapas de las que consta la simulación
-
La bola incidente que se ha desplazado de modo que su centro está a una altura de 1 cm, se suelta y se mueve hasta que choca con la segunda bola. Su velocidad en el momento del choque es
-
Se calcula el desplazamiento y la velocidad de cada una de las bolas que forman la cadena. Se representa:
-
El desplazamiento de cada bola en función del tiempo, activando el botón de radio titulado Desplazamiento
-
La velocidad de cada bola en función del tiempo, activando el botón de radio titulado Velocidad.
-
La fuerza neta que se ejerce sobre cada una de las bolas, activando el botón de radio titulado Fuerza.
-
La bola final se desplaza hasta que su centro se eleva a una altura h'.
A la derecha, se representa mediante un diagrama de barras, la energía cinética del c.m. del sistema formado por n-bolas, y se la compara con la energía cinética inicial (rectángulo de color negro). Vemos que la energía cinética disminuye ya que parte de la energía inicial se convierte en energía de deformación de las bolas elásticas y luego, aumenta, hasta que alcanza el valor inicial. Las pequeñas diferencias se pueden atribuir a la inexactitud de los procedimientos numéricos empleados.
Los cambios de color de la barra nos suministran una imagen visual de la propagación de la perturbación a lo largo de la cadena de bolas.
La segunda barra, representa el momento lineal del sistema formado por n-bolas, el momento lineal inicial está representado por un rectángulo de color negro. El momento lineal se propaga a lo largo de la cadena. El momento lineal final es aproximadamente igual al momento lineal inicial.
Nota: Para describir las tres etapas se han tomado dos escalas de tiempo. Para describir el movimiento de la primera y última bola se ha tomado un intervalo de tiempo de 10-3 s. Para describir el movimiento de las n-bolas en contacto se ha tomado un intervalo de 10-6 s.
Referencias
Herman F, Seitz M., How the ball-chain work?. Am. J. Phys. 50 (11) November 1982, pp. 977-981

