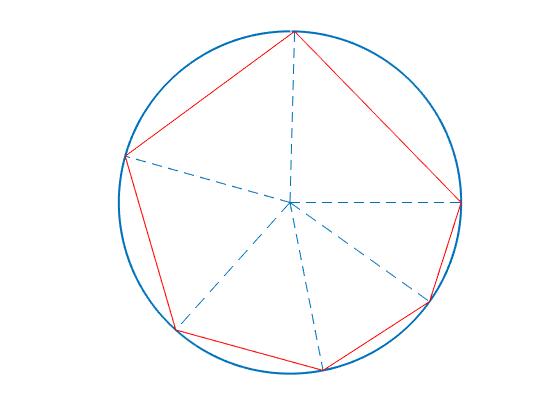
Rebotes en un recinto circular

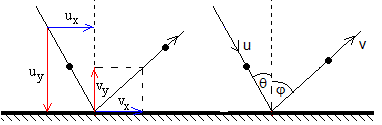
Cuando una pelota rebota sobre un tablero rígido, la componente de la velocidad perpendicular al tablero disminuye su valor, quedando la componente paralela inalterada

v_x=u_xv_y=-e·u_y

o bien

vsinφ=usinθ
vcosφ=e·usinθ

Conocida la velocidad inicial u, el ángulo de incidencia θ y el coeficiente de restitución e, despejamos el ángulo φ y la velocidad de rebote v

$\tan φ = \frac{1}{e} \tan θ v = u \frac{\sin θ}{\sin φ}$

Polígono de tres lados, dos rebotes

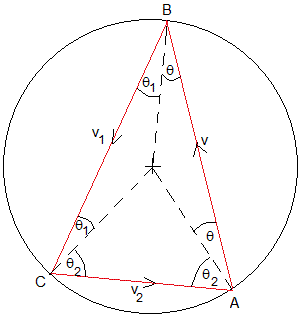
La partícula sale de A con velocidad v, formando un ángulo θ con la dirección radial, choca con el recinto circular en B, en el que se cumple que

$\tan θ_{1} = \frac{1}{e} \tan θ v_{1} = v \frac{\sin θ}{\sin θ_{1}}$

La partícula sale de B con velocidad v₁ haciendo un ángulo θ₁ con la dirección radial y choca con el recinto circular en C, se cumple que

$\begin{array}{l} \tan θ_{2} = \frac{1}{e} \tan θ_{1} v_{2} = v_{1} \frac{\sin θ_{1}}{\sin θ_{2}} \\ \tan θ_{2} = \frac{1}{e^{2}} \tan θ \end{array}$

Como e<1 entonces θ₂>θ₁>θ

Para que la partícula retorne a A y se cierre la trayectoria se tendrá que cumplir que la suma de los ángulos interiores del triángulo sea 180°

2θ+2θ₁+2θ₂=π

$\begin{array}{l} \tan (θ_{1} + θ_{2}) = \tan (\frac{π}{2} - θ) \\ \frac{\tan θ_{1} + \tan θ_{2}}{1 - \tan θ_{1} \cdot \tan θ_{2}} = \frac{1}{\tan θ} \\ \frac{e^{- 1} \tan θ + e^{- 2} \tan θ}{1 - e^{- 3} \tan^{2} θ} = \frac{1}{\tan θ} \\ (\frac{1}{e} + \frac{1}{e^{2}} + \frac{1}{e^{3}}) \tan^{2} θ = 1 \end{array}$

Dado el coeficiente de restitución e, despejamos el ángulo θ que hace que la trayectoria sea cerrada en forma de triángulo

n=2; %número de choques, polígono de n+1 lados
e=0.6; %coeficiente de restitución
th_0=atan(1/sqrt(1/e+1/e^2+1/e^3));
 
hold on
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi], 'lineWidth',1.5)
ang=0;
for k=0:n
    th=atan(tan(th_0)/e^k);
    line([0,cos(ang)],[0,sin(ang)], 'lineStyle','--')
    line([cos(ang),cos(ang+pi-2*th)],[sin(ang),sin(ang+pi-2*th)],'color','r')
    ang=ang+pi-2*th;
end
hold off
grid on
axis equal
axis off

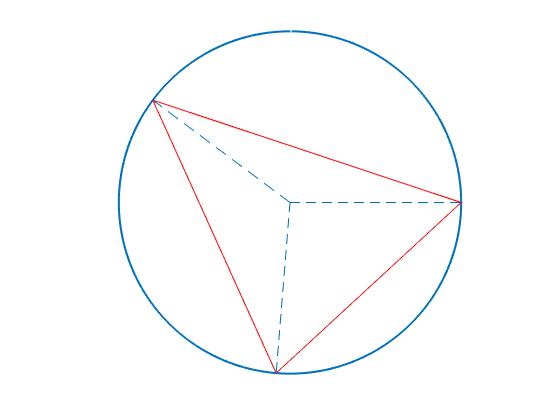
Polígono de cuatro lados, tres rebotes

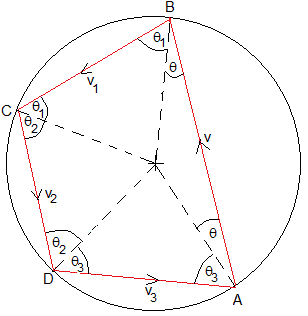
La partícula sale de A con velocidad v, formando un ángulo θ con la dirección radial, choca con el recinto circular en B, en el que se cumple que

$\tan θ_{1} = \frac{1}{e} \tan θ v_{1} = v \frac{\sin θ}{\sin θ_{1}}$

La partícula sale de B con velocidad v₁ haciendo un ángulo θ₁ con la dirección radial y choca con el recinto circular en C, se cumple que

$\begin{array}{l} \tan θ_{2} = \frac{1}{e} \tan θ_{1} v_{2} = v_{1} \frac{\sin θ_{1}}{\sin θ_{2}} \\ \tan θ_{2} = \frac{1}{e^{2}} \tan θ \end{array}$

La partícula sale de C con velocidad v₂ haciendo un ángulo θ₂ con la dirección radial y choca con el recinto circular en D, se cumple que

$\begin{array}{l} \tan θ_{3} = \frac{1}{e} \tan θ_{2} v_{3} = v_{2} \frac{\sin θ_{2}}{\sin θ_{3}} \\ \tan θ_{3} = \frac{1}{e^{3}} \tan θ \end{array}$

Como e<1 entonces θ₃>θ₂>θ₁>θ

Para que la partícula retorne a A y se cierre la trayectoria se tendrá que cumplir que la suma de los ángulos interiores del cuadrilátero sea 360°

2θ+2θ₁+2θ₂+2θ₃=2π

$\begin{array}{l} \tan (θ_{2} + θ_{3}) = \tan (π - (θ + θ_{1})) \\ \tan (θ_{2} + θ_{3}) = - \tan (θ + θ_{1}) \\ \frac{\tan θ_{2} + \tan θ_{3}}{1 - \tan θ_{2} \cdot \tan θ_{3}} = - \frac{\tan θ + \tan θ_{1}}{1 - \tan θ \cdot \tan θ_{1}} \\ \frac{e^{- 2} \tan θ + e^{- 3} \tan θ}{1 - e^{- 5} \tan^{2} θ} = - \frac{\tan θ + e^{- 1} \tan θ}{1 - e^{- 1} \tan^{2} θ} \\ \tan^{2} θ = e^{3} \end{array}$

Dado el coeficiente de restitución e, despejamos el ángulo θ que hace que la trayectoria sea cerrada en forma de cuadrilátero

n=3; %número de choques, polígono de n+1 lados
e=0.6; %coeficiente de restitución
th_0=atan(e^(3/2));
 
hold on
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi], 'lineWidth',1.5)
ang=0;
for k=0:n
    th=atan(tan(th_0)/e^k);
    line([0,cos(ang)],[0,sin(ang)], 'lineStyle','--')
    line([cos(ang),cos(ang+pi-2*th)],[sin(ang),sin(ang+pi-2*th)],'color','r')
    ang=ang+pi-2*th;
end
hold off
grid on
axis equal
axis off

Polígono de n+1 lados, n rebotes

En general, para n colisiones de la partícula con el recinto circular

2θ+2θ₁+2θ₂+...+2θ_n=(n-1)π

$\begin{array}{l} 2 (θ + \sum_{k = 1}^{n} θ_{k}) = (n - 1) π \\ \tan θ_{k} = \frac{1}{e^{k}} \tan θ \end{array}$

Dado el coeficiente de restitución e, resolvemos la ecuación trascendente utilizando el la función fzero de MATLAB

$θ + \sum_{k = 1}^{n} \arctan (\frac{1}{e^{k}} \tan θ) = (n - 1) \frac{π}{2}$

n=5; %número de choques, polígono de n+1 lados
e=0.8; %coeficiente de restitución
 
k=1:n;
f=@(x) x+sum(atan(tan(x)./e.^k))-(n-1)*pi/2;
th_0=fzero(f,[0,pi/2]);
 
hold on
fplot(@(t) cos(t), @(t) sin(t),[0,2*pi], 'lineWidth',1.5)
ang=0;
for k=0:n
    th=atan(tan(th_0)/e^k);
    line([0,cos(ang)],[0,sin(ang)], 'lineStyle','--')
    line([cos(ang),cos(ang+pi-2*th)],[sin(ang),sin(ang+pi-2*th)],'color','r')
    ang=ang+pi-2*th;
end
hold off
axis equal
axis off