El frontón

Supondremos que la resistencia del aire no afecta a la trayectoria de la pelota y que ésta se comporta como una partícula.

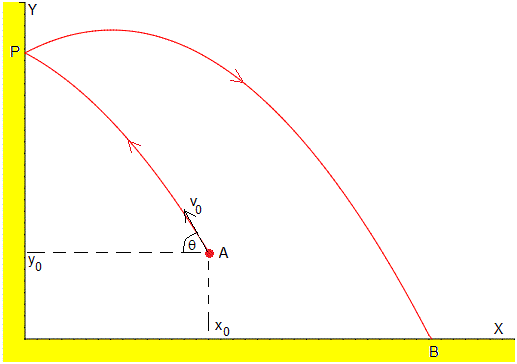
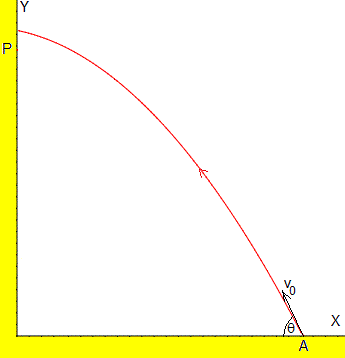
Situamos el eje Y en el frontón y el eje X en el suelo. La pelota se lanza desde la posición A a x₀ de distancia al frontón y a una altura y₀ sobre el suelo, con una velocidad inicial v₀, haciendo un ángulo θ<90, tal como se aprecia en la figura.

Trayectoria de ida

La ecuación del movimiento de la pelota hasta su impacto en P es

${\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = - v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} {\begin{cases} x = x_{0} - v_{0} \cos θ \cdot t \\ y = y_{0} + v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

El choque con el frontón se produce cuando x=0, en el instante t₁

$t_{1} = \frac{x_{0}}{v_{0} \cos θ}$

Choque con el frontón

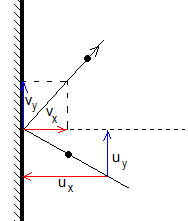
La altura y_P de P y las componentes (u_x, u_y) de la velocidad de la pelota en P antes del choque son:

${\begin{cases} u_{x} = - v_{0} \cos θ \\ u_{y} = v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ} \end{cases} {\begin{cases} x_{P} = 0 \\ y_{P} = y_{0} + x_{0} \tan θ - \frac{1}{2} g \frac{x_{0}^{2}}{v_{0}^{2} \cos^{2} θ} \end{cases}$

La componente vertical de la velocidad no cambia, v_y=u_y, y la componente horizontal de la velocidad se reduce en módulo y cambia de signo. v_x=-e·u_x

Trayectoria de vuelta

Esta es la velocidad inicial de la pelota después de rebotar en P. La ecuación del movimiento de la pelota desde P hasta que llega al suelo en B es

${\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = - e u_{x} \\ v_{y} = u_{y} - g t \end{cases} {\begin{cases} x = - e u_{x} \cdot t \\ y = y_{P} + u_{y} \cdot t - \frac{1}{2} g t^{2} \end{cases}$

La pelota llega al suelo en el instante t₂, cuando y=0

$t_{2} = \frac{u_{y} + \sqrt{u_{y}^{2} + 2 g y_{P}}}{g}$

La distancia x_B del punto B al frontón es

$\begin{array}{l} x_{B} = - e u_{x} \frac{u_{y} + \sqrt{u_{y}^{2} + 2 g y_{P}}}{g} = \\ \frac{e v_{0} \cos θ}{g} (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ} + \sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}) \end{array}$

la medida de x_B nos daría el coeficiente de restituación e

Ejemplos

Supongamos que los choques de la pelota con el frontón son elásticos de modo que e=1

Fijamos la posición de partida de la pelota en A, a una distancia x₀=3 m del frontón y a una altura y₀=1.5 m sobre el suelo. Fijamos también, el ángulo de tiro, θ=60°.

Para que la pelota llegue al frontón y rebote, la velocidad v₀, tiene que ser mayor que un valor mínimo.

El valor mínimo de v₀ se calcula poniendo x=0, e y=0, en la ecuación del movimiento de la pelota en la trayectoria de ida, de A a P

${\begin{cases} x = x_{0} - v_{0} \cos θ \cdot t \\ y = y_{0} + v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

Despejemos v₀

$v_{\min} = \frac{x_{0}}{\cos θ} \sqrt{\frac{g}{2 (y_{0} + x_{0} \tan θ)}}$

El resultado es v_mín=5.13 m/s. Por debajo de esa velocidad, la pelota lanzada desde A con ángulo θ=60° no llega a tocar el frontón

Supongamos que lanzamos la pelota con velocidad v₀=10 m/s

x0=3; %posición de lanzamiento
y0=1.5;
e=1; %coeficiente de restitución
theta=pi/3; %ángulo de tiro
v0=10; %velocidad inicial
v0_x=-v0*cos(theta);
v0_y=v0*sin(theta);
%v_min=x0*sqrt(4.9/(y0+x0*tan(theta)))/cos(theta)

hold on
%trayectoria de ida
t1=-x0/v0_x;
x=@(t) x0+v0_x*t;
y=@(t) y0+v0_y*t-4.9*t.^2;
fplot(x,y,[0,t1])
if y(t1)>0 
    %rebote en el frontón
    x0=0;
    v0_x=-e*v0_x;
    y0=y(t1);
    v0_y=v0_y-9.8*t1;
    %trayectoria de vuelta
    t2=(v0_y+sqrt(v0_y^2+2*9.8*y0))/9.8;
    x=@(t) x0+v0_x*t;
    y=@(t) y0+v0_y*t-4.9*t.^2;
    fplot(x,y,[0,t2])
end
hold off
xlim([0,10])
ylim([0,7])
xlabel('x')
ylabel('y')
title('juego de la pelota en el frontón')
grid on

>> t1
t1 =    0.6000
>> y0
y0 =    4.9322
>> t2
t2 =    1.3263
>> x(t2)
ans =    6.6316

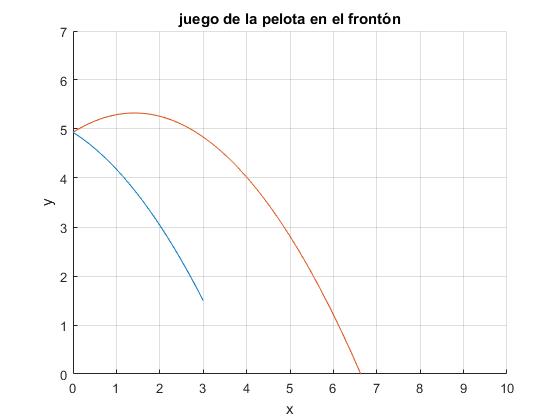
La pelota tarda un tiempo t₁=0.6 s en alcanzar el frontón a una altura y_P=4.93 m.

La pelota impacta en el suelo en el punto B después de un tiempo t₂=1.33 s, a una distancia x_B=6.63 m del frontón.

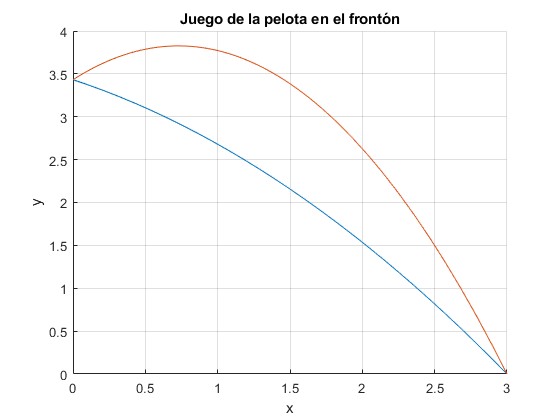
Las trayectorias se superponen

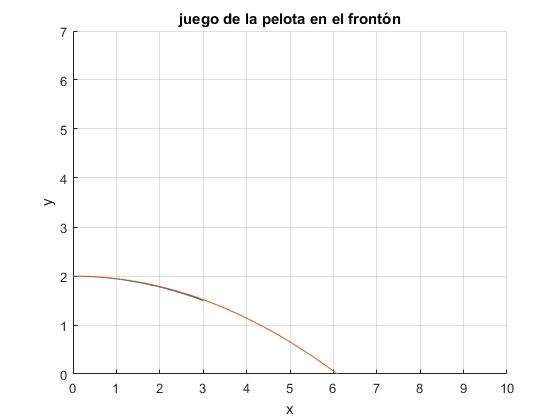
Calculamos ahora, el ángulo θ para el cual las trayectorias de ida y vuelta se superponen. Para que esto ocurra la componente vertical de la velocidad u_y en el punto de impacto deberá ser cero

$\begin{array}{l} u_{y} = v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ} \\ \sin (2 θ) = 2 g \frac{x_{0}}{v_{0}^{2}} \end{array}$

Con los datos de este ejemplo, θ=18.2° y choca con el suelo a una distancia x_B=6.09 m del frontón

>> t1
t1 =    0.3158
>> y0
y0 =    1.9977
>> t2
t2 =    0.6414
>> x(t2)
ans =    6.0933

Alcance

Finalmente, investigamos la variación del alcance x_B con el ángulo de tiro, θ, manteniendo fijos la posición inicial (x₀, y₀) de la pelota y la velocidad de lanzamiento v₀. Veremos que x_B crece con el ángulo y luego, decrece, alcanzando un valor máximo para el ángulo de tiro θ_m.

Para calcularlo, derivamos x_B respecto de θ y lo igualamos a cero

$\begin{array}{l} x_{B} = \frac{e v_{0} \cos θ}{g} (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ} + \sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}) \\ \frac{d x_{B}}{d θ} = - \frac{e v_{0} \sin θ}{g} (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ} + \sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}) + \frac{e v_{0} \cos θ}{g} (v_{0} \cos θ - g \frac{x_{0} \sin θ}{v_{0} \cos^{2} θ} + \frac{v_{0}^{2} \sin θ \cos θ}{\sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}}) \\ = \frac{e v_{0}^{2}}{g} (\cos^{2} θ - \sin^{2} θ) + \frac{e v_{0} \sin θ}{g} (\frac{v_{0}^{2} \cos^{2} θ}{\sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}} - \sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}) \\ = \frac{e v_{0}^{2}}{g} \cos (2 θ) + \frac{e v_{0} \sin θ}{g} (\frac{v_{0}^{2} \cos^{2} θ}{\sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}} - \sqrt{2 g y_{0} + v_{0}^{2} \sin^{2} θ}) = 0 \end{array}$

Calculamos la raíz θ_m de la ecuación transcendente utilizando la función fzero de MATLAB

e=1; %coeficiente de restitución
v0=10; %velocidad inicial
x0=3; %posición de lanzamiento
y0=1.5;
angulos=(5:80)*pi/180;
f=@(x) e*v0*cos(x).*(v0*sin(x)-9.8*x0./(v0*cos(x))+sqrt(19.6*y0+
(v0*sin(x)).^2))/9.8;
alcance=f(theta);
plot(angulos,alcance)
%máximo
g=@(x) e*v0^2*cos(2*x)/9.8+(e*v0*sin(x)/9.8).*(v0^2*cos(x).^2.
/sqrt(19.6*y0+(v0*sin(x)).^2)-sqrt(19.6*y0+(v0*sin(x)).^2));
th_m=fzero(g,[0,pi/2]);
line([th_m,th_m],[0,f(th_m)], 'lineStyle','--')
disp(th_m*180/pi)
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta')
ylabel('x_B')
title('Juego de la pelota en el frontón')
grid on

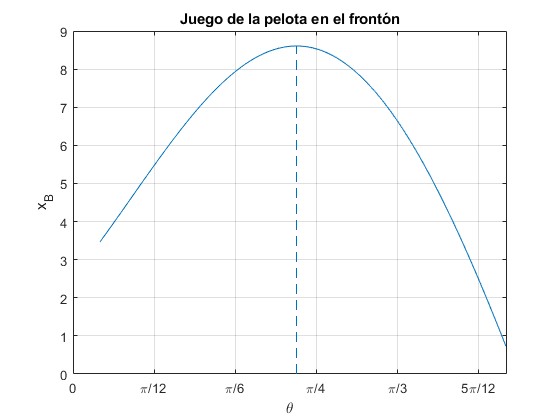
Para el ángulo de tiro θ=41.3° x_B alcanza el máximo

   41.3183

Actividades

Se introduce

La velocidad inicial de la pelota en A, v₀, en el control titulado Velocidad
El ángulo de tiro, θ, en el control titulado Angulo
El coeficiente de restitución e, del choque de la pelota con el frontón, en el control titulado Coeficiente restitución. En un choque elástico e=1.

Se pulsa el botón titulado Nuevo

Con el puntero del ratón se arrastra el círculo de color rojo, para establecer la posición inicial de la pelota: la distancia x₀ al frontón y su altura sobre el suelo y₀. El rectángulo de color rojo marca los límites de la altura y de la distancia. Por defecto, x₀=3 m e y₀=1.5 m

Se pulsa el botón titulado empieza ►

Se observa la trayectoria de la pelota, en la parte superior se proporcionan los datos de su posición x (distancia frontón) e y (altura sobre el suelo). Cuando llega al suelo medimos el alcance x_B

Velocidad: Angulo:
Coeficiente restitución:

La pelota regresa al punto de partida

Supongamos que la pelota parte de la poisición A (x₀, 0) y se lanza con con velocidad v₀, haciendo un ángulo θ con la horizontal, tal como se muestra en la figura

Vamos a calcular el coeficiente de restitución e que hace que la pelota regrese al punto A de partida

Posición de la pelota en el movimiento de ida

${\begin{cases} x = x_{0} - v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

El tiempo que tarda en llegar al frontón es

$t_{1} = \frac{x_{0}}{v_{0} \cos θ}$

La altura del punto P de impacto es

$y_{P} = x_{0} \tan θ - \frac{1}{2} g \frac{x_{0}^{2}}{v_{0}^{2} \cos^{2} θ}$

La posición de la pelota en la trayectoria de vuelta, después del choque con el frontón (véase el primer apartado) es

$\begin{array}{l} {\begin{cases} x = - e u_{x} t \\ y = y_{P} + u_{y} t - \frac{1}{2} g t^{2} \end{cases} \\ {\begin{cases} x = e v_{0} \cos θ \cdot t \\ y = y_{P} + (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ}) t - \frac{1}{2} g t^{2} \end{cases} \end{array}$

El tiempo de vuelta es

$t_{2} = \frac{x_{0}}{e v_{0} \cos θ}$

Como la altura de A es y=0

$\begin{array}{l} y_{P} + (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ}) t_{2} - \frac{1}{2} g t_{2}^{2} = 0 \\ x_{0} \tan θ - \frac{1}{2} g \frac{x_{0}^{2}}{v_{0}^{2} \cos^{2} θ} + (v_{0} \sin θ - g \frac{x_{0}}{v_{0} \cos θ}) t_{2} - \frac{1}{2} g t_{2}^{2} = 0 \end{array}$

Sustituyendo t₂ y simplificando

$\begin{array}{l} \sin θ (1 + \frac{1}{e}) = \frac{1}{2} g \frac{x_{0}}{v_{0}^{2} \cos θ} {(1 + \frac{1}{e})}^{2} \\ e = \frac{g x_{0}}{v_{0}^{2} \sin 2 θ - g x_{0}} \end{array}$

Sea

Posición de partida: x₀=3 m, y₀=0
Velocidad de lanzamiento, x₀=10 m/s
Angulo de tiro, θ=π/3, (60°)

x0=3; %distancia al frontón
v0=10; %velocidad de lanzamiento
th=pi/3; %ángulo de tiro
e=9.8*x0/(v0^2*sin(2*th)-9.8*x0); %coeficiente de restitucion
hold on
%trayectoria de ida
t1=x0/(v0*cos(th));
x=@(t) x0-v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
fplot(x,y,[0,t1])
%trayectoria de vuelta
t2=x0/(e*v0*cos(th));
x=@(t) e*v0*cos(th)*t;
y=@(t) x0*tan(th)-4.9*x0^2*(1+tan(th)^2)/v0^2+(v0*sin(th)-9.8*x0/
(v0*cos(th)))*t-4.9*t.^2;
fplot(x,y,[0,t2])
hold off
xlabel('x')
ylabel('y')
title('Juego de la pelota en el frontón')
grid on

El coeficiente de restitución es e=0.5140

0.5140

Se sugiere al lector probar en el programa interactivo, que la trayectoria de vuelta pasa por la posición de lanzamiento de la pelota.

Referencias

Indian National Physics Olympiad. Homi Bhabha Centre for Science Eduaction. Solved papers NSEP & INPhO, 2016-2018, Example 34, pp. 29