Sucesivos rebotes en dos planos inclinados

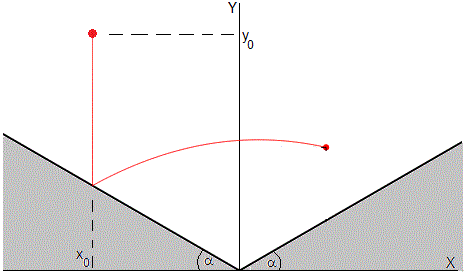
Vamos a analizar cada una de las etapas del movimiento de la partícula

Movimiento vertical de la partícula

En la primera etapa del movimiento, la partícula cae desde una altura y₀ y choca con el plano inclinado en el punto (x₀, -x₀tanα). La ecuación del movimiento es

${\begin{cases} x = x_{0} \\ y = y_{0} - \frac{1}{2} g t^{2} \end{cases}$

El tiempo que tarda en chocar con el plano inclinado es

$t_{1} = \sqrt{\frac{2 (y_{0} + x_{0} \tan α)}{g}} x_{0} < 0$

La velocidad con la que llega al punto de impacto es en módulo, v₁=gt₁

Choque con el plano inclinado, x<0

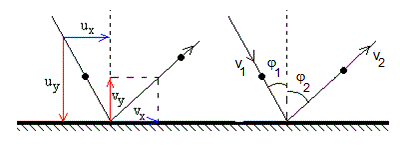
Cuando una pelota rebota sobre un tablero rígido, la componente de la velocidad perpendicular al tablero disminuye su valor, quedando la componente paralela inalterada

v_x=u_xv_y=-e·u_y

o bien

v₂sinφ₂= v₁sinφ₁
v₂cosφ₂= e·v₁cosφ₁

$\tan φ_{2} = \frac{1}{e} \tan φ_{1} v_{2} = v_{1} \frac{\sin φ_{1}}{\sin φ_{2}}$

Como el coeficiente de restitución e<1, el ángulo de incidencia φ₁<φ₂

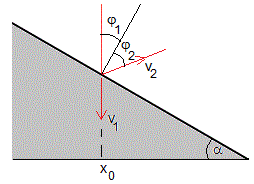
El tablero no está horizontal, sino inclinado un ángulo α. El ángulo de incidencia que hace la dirección de la velocidad con la normal al plano inclinado, φ₁=α que es el ángulo del plano inclinado

$\tan φ_{2} = \frac{1}{e} \tan φ_{1} v_{2} = v_{1} \frac{\sin φ_{1}}{\sin φ_{2}}$

La velocidad de rebote v₂ es la velocidad inicial v₀ de la partícula y θ₀=π/2-φ₁-φ₂=π/2-α-φ₂ es el ángulo de tiro, tal como vemos en la figura más abajo

Trayectoria parabólica

La partícula parte de la posición (x₀, y₀), con velocidad inicial v₀, haciendo un ángulo θ₀ con la horizontal

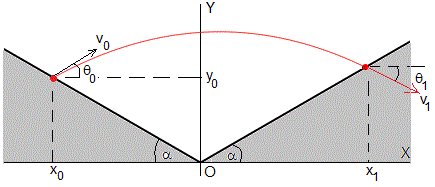
Las ecuaciones del movimiento de la partícula son

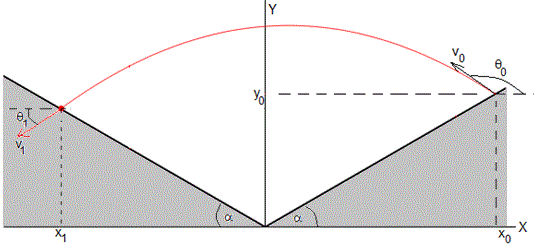
$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g t \end{cases} \vec{r} {\begin{cases} x = x_{0} + v_{0} \cos θ \cdot t \\ y = y_{0} + v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

Dependiendo del ángulo de tiro y la velocidad de disparo, la partícula puede chocar con el primer plano inclinado o el segundo. Supongamos que choca con el segundo plano inclinado, tal como se muestra en la figura.

Primero, calculamos el tiempo de vuelo T, el punto de impacto (x₁, x₁·tanα), la velocidad final v₁ y su dirección θ₁. El punto de impacto es la intersección entre la trayectoria parabólica y la recta y=x·tanα

$\begin{array}{l} y_{0} + v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} = (x_{0} + v_{0} \cos θ \cdot t) \tan α \\ \frac{1}{2} g t^{2} + v_{0} (\cos θ \cdot \tan α - \sin θ) t - y_{0} + x_{0} \tan α = 0 \end{array}$

El tiempo de vuelo T es la raíz positiva de esta ecuación de segundo grado
El punto de impacto es, x₁=x₀+x₀cosθ·T, y₁=x₁·tanα
Las componentes de la velocidad de la partícula en el punto de impacto son:

$\begin{array}{l} \vec{v_{1}} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} \sin θ - g T \end{cases} \\ v_{1} = \sqrt{v_{x}^{2} + v_{y}^{2}} \tan θ_{1} = \frac{| v_{y} |}{v_{x}} \end{array}$

Choque con el plano inclinado x>0

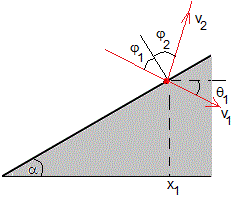
Como vemos en la figura, el angulo incidente, que hace la dirección de la velocidad con la normal al plano inclinado, φ₁=π/2-α-θ₁

$\tan φ_{2} = \frac{1}{e} \tan φ_{1} v_{2} = v_{1} \frac{\sin φ_{1}}{\sin φ_{2}}$

La velocidad de rebote v₂ es la velocidad inicial v₀ de la partícula y θ=π/2+α-φ₂ es el ángulo de tiro, para la siguiente trayectoria parabólica.

Trayectoria parabólica

Otras posibles trayectorias parabólicas parten del segundo plano inclinado e impactan sobre este plano inclinado o sobre el primero. Un ejemplo, se muestra en la figura

Choque con el plano inclinado x<0

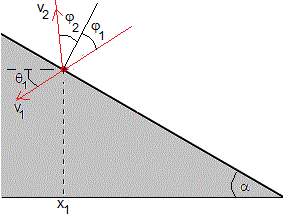
Como vemos en la figura, el angulo incidente φ₁=π/2-α-θ₁

$\tan φ_{2} = \frac{1}{e} \tan φ_{1} v_{2} = v_{1} \frac{\sin φ_{1}}{\sin φ_{2}}$

La velocidad de rebote v₂ es la velocidad inicial v₀ de la partícula y θ=π-(π/2+α-φ₂)=π/2-α+φ₂, es el ángulo de tiro.

Quedan por analizar las trayectorias parabólicas entre dos puntos del mismo plano inclinado

Cálculo con MATLAB

e=0.9; %coeficiente de restitución
angulo=pi/6; %ángulo del plano inclinado
n=5; %número de trayectorias parabólicas
x0=-1; %posición inicial
y0=2;

hold on
%planos inclinados
line([0,-2],[0,2*tan(angulo)],'lineWidth',1.5','color','k')
line([0,2],[0,2*tan(angulo)],'lineWidth',1.5','color','k')

t0=sqrt(2*(y0+x0*tan(angulo))/9.8); %tiempo del primer choque
vy=9.8*t0; %velocidad antes del choque
vx=eps;  %cero
line([x0,x0],[y0,-x0*tan(angulo)], 'color','r') %trayectoria vertical
y0=-x0*tan(angulo);

for k=0:n % n trayectorias
    %choque
    alfa=-angulo*sign(x0);
    th_1=atan(abs(vy/vx));
    phi_1=pi/2-th_1+alfa*sign(vx);
    phi_2=atan(tan(phi_1)/e);
%velocidad inicial y ángulo de tiro
    v0=sqrt(vx^2+vy^2)*sin(phi_1)/sin(phi_2);
    th_0=pi/2-alfa-sign(vx)*phi_2;
%tiempo de vuelo de la trayectorias parabólica
    sgn=1; %1 es x>0  y -1 es x>0
    b=-v0*(cos(th_0)*tan(angulo*sgn)+sin(th_0));
    c=-x0*tan(angulo*sgn)-y0;
    t1=(-b+sqrt(b*b-4*4.9*c))/9.8;
    z=x0+v0*cos(th_0)*t1;
    if z>0 
        sgn=-1; %1 es x>0  y -1 es x>0
        b=-v0*(cos(th_0)*tan(angulo*sgn)+sin(th_0));
        c=-x0*tan(angulo*sgn)-y0;
        t1=(-b+sqrt(b*b-4*4.9*c))/9.8;
    end  
 %trayectoria
    fplot(@(t) x0+v0*cos(th_0)*t, @(t) y0+v0*sin(th_0)*t-4.9*t.^2,[0,t1],'color','r')
%posición del punto de impacto y velocidad en esta posición
    x0=x0+v0*cos(th_0)*t1;
    y0=y0+v0*sin(th_0)*t1-4.9*t1^2;
    vx=v0*cos(th_0);
    vy=v0*sin(th_0)-9.8*t1;
end
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Rebotes en dos planos inclinado')

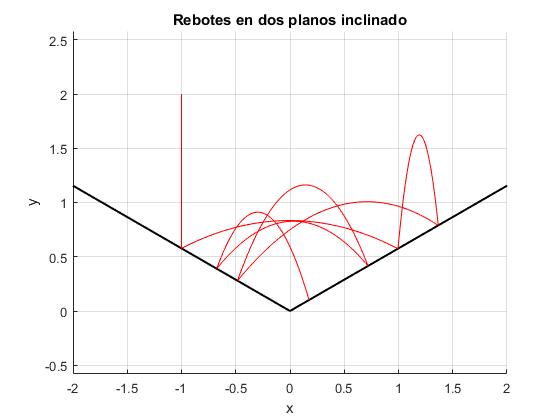
Actividades

Se introduce

El ángulo de los planos inclinados en el control titulado Plano inclinado
El coeficiente de restitución en el control titulado Coef. restitución

Se pulsa el botón titulado Nuevo

Se observa las trayectorias parabólicas entre dos puntos del mismo plano inlinado, o de distintos planos inclinados

En la parte superior izquierda, se proporcionan los datos del tiempo t, las coordenadas de la partícula (x, y), y en la parte derecha, una barra de color rojo, nos indica la energía de la partícula. Cuando los choques son elásticos e=1, la energía total de la partícula se mantiene constante, cuando e<1, la energía disminuye en el momento del choque con los planos.

Plano inclinado
Coef. restitución