Un proyectil disparado por un carro de combate en movimiento
Vamos a estudiar distintos casos en orden de dificultad creciente, hasta llegar al más general, cuando el carro se mueve con velocidad V y se dispara el proyectil con un ángulo de tiro θ
El carro está firmemente sujeto al suelo, el disparo es horizontal
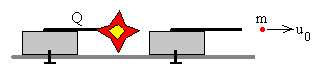
Supongamos que el carro está firmemente sujeto al suelo y se dispara un proyectil de masa m. La velocidad u0 de salida del proyectil es
El sistema formado por el carro y el proyectil no es aislado.
El carro está en reposo sobre el suelo, el disparo es horizontal
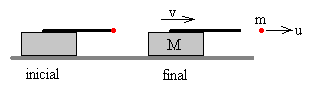
La masa del carro incluido el cañón vacío es M, y puede moverse sin rozamiento sobre una pista horizontal.
El sistema formado por el carro y el proyectil es aislado. Aplicamos el principio de conservación del momento lineal
-
El momento lineal inicial es cero
-
El momento lineal final es Mv+mu
El carro se mueve en la misma dirección que el proyectil pero en sentido contrario
La parte Q de la energía de combustión de la pólvora en el ánima del cañón se convierte en energía cinética del proyectil y del carro. El balance energético se escribe
Despejamos la velocidad u del proyectil y v de retroceso del carro
Cuando la masa M del carro es muy grande comparada con la masa m del proyectil, la velocidad de retroceso v→0 y la velocidad del proyectil u→u0.
El carro se mueve con velocidad constante V antes del disparo, el disparo es horizontal
Si el carro se mueve con velocidad constante V en una pista horizontal, después del disparo
-
La velocidad del proyectil respecto de Tierra será u'=u+V
-
La velocidad del carro respecto de Tierra v'=v+V
Se cumple el principio de conservación del momento lineal
(M+m)V=Mv'+mu'
(M+m)V=M(v+V)+m(u+V)
Se cumple la ecuación del balance energético
Calculamos las velocidades u' y v' después del disparo despejándolas del sistema de dos ecuaciones como en el caso anterior.
El resultado es el mismo que obtuvimos anteriormente
El carro está en reposo y el ángulo de tiro es θ
El carro está inicialmente en reposo y se fija el ángulo θ de tiro. Se dispara el proyectil
El momento lineal tiene dos componentes: una horizontal y otra vertical.
El sistema formado por el proyectil y el carro no es aislado en la dirección vertical, pero si lo es en la dirección horizontal.
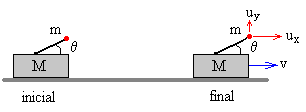
En la dirección vertical el carro se encuentra fijo al suelo (primer caso estudiado), por tanto, la componente vertical de la velocidad del proyectil es uy=u0·sinθ.
En la dirección horizontal el momento lineal se conserva.
-
El momento lineal inicial es cero
-
El momento lineal final es Mv+mux
Donde ux es la velocidad horizontal del proyectil
La ecuación del balance energético se escribe
Despejamos la componente horizontal de la velocidad del proyectil ux y la velocidad de retroceso del carro v.
El carro se mueve con velocidad V antes del disparo y el ángulo de tiro es θ
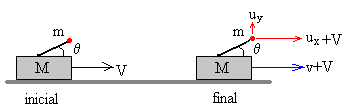
Si el carro se mueve con velocidad constante V antes del disparo
Las componentes de la velocidad del proyectil cuando sale del cañón serán
La velocidad del carro después del disparo será
Establecemos un sistema de referencia inmóvil en la boca del cañón en el momento en el que es disparado el proyectil.
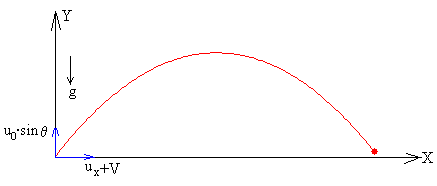
Escribimos las ecuaciones del movimiento de un proyectil bajo la aceleración constante de la gravedad cuyas velocidades iniciales son
-
ux+V en la dirección horizontal X
-
uy en la dirección vertical Y.
El alcance del proyectil se obtiene cuando y=0.
El cañón siempre dispara hacia adelante, pero el carro puede moverse hacia adelante o hacia atrás. Cuando se mueve hacia atrás V<0, para un determinado ángulo de tiro θ la componente horizontal ux+V de la velocidad es nula, el alcance horizontal x es nulo, el proyectil sube y baja a lo largo del eje Y.
Ejemplo 1:
-
Angulo de disparo θ=45º
-
Velocidad de disparo del proyectil u0=100 m/s cuando el carro está fijado al suelo
-
Velocidad del carro V=30 m/s
-
Cociente entre las masas del carro y del proyectil M/m=5.0
La velocidad del carro después del disparo es
Las componentes de la velocidad del proyectil son
Comprobamos que se cumple el balance energético
El alcance es
Ejemplo 2:
-
Velocidad de disparo del proyectil u0=100 m/s cuando el carro está fijo al suelo
-
Velocidad del carro V=-30 m/s, se mueve hacia la izquierda.
-
Cociente entre las masas del carro y del proyectil M/m=5.0
Para el ángulo de disparo θ tal que ux+V=0, o bien,
El alcance horizontal xm=0
La velocidad de retroceso del carro vale
Actividades
Se introduce
-
El ángulo θ de tiro, en el control titulado Ángulo
-
La velocidad V del carro de combate antes del disparo, un valor positivo o negativo, en el control titulado Velocidad carro.
-
El cociente M/m, masa del carro entre la masa del proyectil, en el control titulado Masa carro/proyectil.
-
La velocidad del proyectil cuando el carro está fijo al suelo u0=100 m/s
Se pulsa el botón titulado Nuevo
Durante 4 segundos observamos el movimiento del carro de combate, hasta que la boca del cañón se sitúa en el origen del sistema de referencia. En ese instante se produce el disparo. Observamos el movimiento del proyectil y del carro. En la parte derecha, se proporcionan los datos:
- del tiempo t contado a partir del momento del disparo,
- la posición x e y del proyectil,
- la posición x y velocidad v del carro después del disparo.

