Choque inelástico de duración finita (III)

En la página titulada “Un choque inelástico de duración finita” hemos examinado un modelo simplificado que explica lo que ocurre en el pequeño intervalo de tiempo que dura un choque inelástico entre una bala y un bloque. La bala disminuye la velocidad aumenta la del bloque hasta que ambos adquieren la misma velocidad, en ese instante el choque finaliza.

Estudiamos el comportamiento de un sistema aislado formado por dos partículas (la bala y el bloque) que interactuaban mediante una fuerza interna de valor constante que se oponía al movimiento de la bala, pero que favorecía el movimiento del bloque.

En la página titulada "Péndulo balístico" estudiamos el choque instantáneo entre una bala y un bloque, y aplicamos el principio de conservación del momento lineal para obtener la velocidad inmediatamente después del choque, del conjunto formado por la bala y el bloque.

En esta página, se estudia el mismo sistema formado por un bloque y una bala, estando el bloque sujeto por ambos extremos mediante dos varillas de masa despreciable. Si el choque es instantáneo, las fuerzas exteriores se anulan en el momento del choque, pero si es de duración finita, las fuerzas exteriores no se anulan y por tanto, no se puede aplicar el principio de conservación del momento lineal.

Choque inelástico instantáneo

Si el choque es instantáneo, el bloque no se habrá desplazado de su posición vertical inicial, las fuerzas exteriores: el peso (m+M)g y la tensión de la cuerda T se anulan. El sistema es aislado y se puede aplicar el principio de conservación del momento lineal en el momento del choque.

En el momento del choque

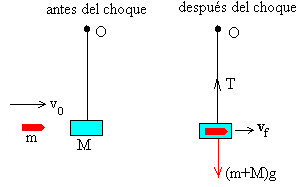
Sea M la masa del bloque inicialmente en reposo y m la masa de la bala, cuya velocidad inmediatamente antes del choque es v₀. La velocidad final v_f del conjunto bala-bloque inmediatamente después del choque es

mv₀=(m+M)v_f

A continuación, se efectúa el balance energético de la colisión. La variación de energía cinética es

$Δ E = E_{f} - E_{i} = \frac{1}{2} (m + M) v_{f}^{2} - \frac{1}{2} m v_{0}^{2} = - \frac{1}{2} \frac{m M}{m + M} v_{0}^{2}$

Movimiento después del choque

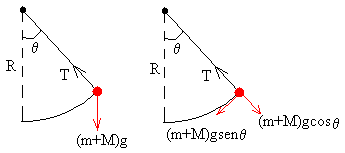
Una vez que el conjunto bala-bloque ha adquirido la velocidad v_f, se desvía de la posición de equilibrio, haciendo un ángulo θ, al cabo de un cierto tiempo t tal como se indica en la figura. Supondremos que el bloque y la bala son masas puntuales.

Descomponemos las fuerzas que actúan sobre sistema a lo largo de la dirección radial y a lo largo de la dirección tangencial

La ecuación del movimiento a lo largo de la dirección radial es

(m+M)a_n=T-(M+m)g·cosθ

donde a_n es la componente normal de la aceleración a_n =v²/R, y R es la longitud del péndulo.

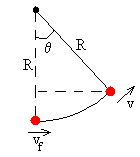
Aplicando el principio de conservación de la energía calculamos la velocidad v cuando el péndulo se ha desviado un ángulo θ después del choque

$\begin{array}{l} \frac{1}{2} (m + M) v_{f}^{2} = \frac{1}{2} (m + M) v^{2} + (m + M) g (R - R \cos θ) \\ v^{2} = v_{f}^{2} - 4 g R \sin^{2} \frac{θ}{2} \end{array}$

Conocido v, se calcula la tensión T de la cuerda

$T = (m + M) \frac{v^{2}}{R} + (m + M) g \cos θ$

El máximo ángulo θ_m<90º que se desvía el péndulo se calcula poniendo v=0, en la ecuación de la conservación de la energía

$\sin (\frac{θ_{m}}{2}) = \frac{v_{f}}{2 \sqrt{g R}}$

La ecuación del movimiento a lo largo de la dirección tangencial es

(m+M)a_t=-(M+m)g·sinθ

donde a_t es la componente tangencial de la aceleración a_t=αR.

La ecuación diferencial del movimiento del péndulo es

$\frac{d^{2} θ}{d t^{2}} + \frac{g}{R} \sin θ = 0$

Con las condiciones iniciales t=0, θ=0, dθ/dt=v_f/R

Se resuelve la ecuación diferencial por procedimientos numéricos, obteniéndose la posición θ, y la velocidad R·dθ/dt en función del tiempo t.

Ejemplo:

En el programa interactivo del péndulo balístico se introducen los siguientes datos:

Masa del bloque M=1.5 kg
Masa de la bala m=0.2 kg
Velocidad de la bala v₀=10 m/s
Longitud del péndulo R=0.5 m

Velocidad del conjunto bloque-bala después del choque

0.2·10=(1.5+0.2)·v_f v_f=1.18 m/s

El ángulo máximo que se desvía el péndulo después del choque es

$\sin (\frac{θ_{m}}{2}) = \frac{v_{f}}{2 \sqrt{g R}} θ_{m} = 2 \cdot \arcsin (\frac{1.18}{2 \sqrt{9.8 \cdot 0.5}}) = 30.8 º$

Choque inelástico de duración finita

Vamos a considerar el sistema formado por una bala de masa m y un bloque de masa M, de forma rectangular de longitud L sujeto por sus extremos mediante dos varillas rígidas de masa despreciable tal como se muestra en la figura.

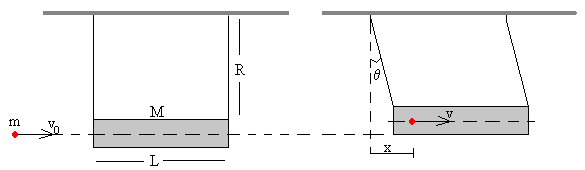
La bala se dispara horizontalmente con velocidad v₀ contra una de las caras del bloque a lo largo de la línea que pasa por su centro de masas (c.m.), penetra en el bloque una cierta distancia hasta que ambos adquieren la misma velocidad. A medida que la bala va penetrando en el bloque, el c.m. del bloque describe un movimiento circular de radio R.

Las fuerzas que actúan sobre este sistema formado por la bala y el bloque son internas (en color azul) y externas (en color rojo) que dibujamos sobre cada uno de los cuerpos.

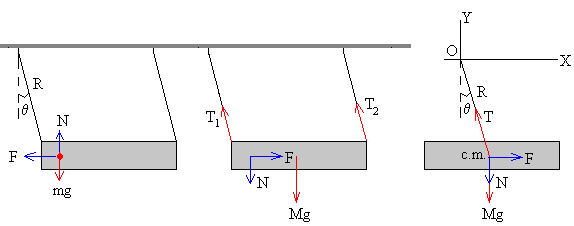
Sobre la bala (a la izquierda de la figura) actúan

La fuerza exterior que es su peso, mg
Una fuerza interior de rozamiento F en dirección opuesta a la velocidad de la bala relativa al bloque.
Una fuerza interior N, que obliga a la bala a moverse a lo largo del eje del bloque en el sistema de referencia ligado al bloque. La fuerza N hace que el movimiento vertical de la bala sea el mismo que el movimiento del c.m. del bloque.

Sobre el bloque (en el centro y derecha de la figura) actúan las siguientes fuerzas

La fuerza exterior Mg que es el peso del bloque y que actúa en su c.m.
La fuerzas T₁ y T₂ que son paralelas y del mismo sentido, que ejercen las varillas que sujetan al bloque, y que podemos sustituir por una única fuerza T=T₁+T₂ en la misma dirección y sentido aplicada en el c.m. del bloque.
Las fuerza interiores F y N obedecen a la tercera ley de Newton tal como se muestra en la figura, tienen el mismo módulo, la misma dirección pero sentido contrario a las dibujadas sobre la bala.

Una vez dibujadas las fuerzas, escribiremos las ecuaciones del movimiento de la bala y del c.m. del bloque, para ello estableceremos un sistema de ejes tal como se indica en la parte derecha de la figura.

Movimiento de la bala

La bala se mueve a lo largo del eje X, bajo la acción de la fuerza que supondremos constante F que se opone a su movimiento.

$\begin{array}{l} m \frac{d v_{x}}{d t} = - F \\ v_{x} = v_{0} - \frac{F}{m} t x = v_{0} t - \frac{1}{2} \frac{F}{m} t^{2} \end{array}$

La componente Y de la velocidad de la bala es la misma que la componente Y de la velocidad del c.m. del bloque v_y=V_y.

$m \frac{d V_{y}}{d t} = N - m g$

Movimiento del bloque

Las ecuaciones del movimiento del c.m. del bloque a lo largo del eje X y del eje Y son respectivamente:

$\begin{array}{l} M \frac{d V_{x}}{d t} = F - T \sin θ \\ M \frac{d V_{y}}{d t} = - N - M g + T \cos θ \end{array}$

Tenemos tres ecuaciones que vamos a combinar para eliminar las fuerzas desconocidas N y T. Sumamos la primera y la tercera para eliminar N.

$\begin{array}{l} M \frac{d V_{x}}{d t} = F - T \sin θ \\ (M + m) \frac{d V_{y}}{d t} = - (M + m) g + T \cos θ \end{array}$

Entres estas dos, eliminamos T.

$M \frac{d V_{x}}{d t} \cos θ + (M + m) \frac{d V_{y}}{d t} \sin θ = F \cos θ - (M + m) g \cdot \sin θ$

que es la ecuación del movimiento del bloque.

Queremos llegar a una ecuación que nos permita calcular el desplazamiento angular θ del c.m. del bloque en función del tiempo t.

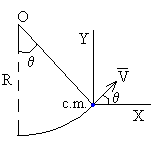
Como vemos en la figura, el vector velocidad $\vec{V}$ del c.m del bloque es tangente a su trayectoria circular de radio R. Las componentes de la velocidad V_x y V_y son

V_x=V·cos θ
V_y=V·sin θ

y sus derivadas respecto del tiempo t

$\begin{array}{l} \frac{d V_{x}}{d t} = \frac{d V}{d t} \cos θ - V \sin θ \frac{d θ}{d t} \\ \frac{d V_{y}}{d t} = \frac{d V}{d t} \sin θ + V cos θ \frac{d θ}{d t} \end{array}$

De la relación entre magnitudes lineales y angulares tenemos que V=R·dθ/dt

$\begin{array}{l} \frac{d V_{x}}{d t} = R \frac{d^{2} θ}{d t^{2}} \cos θ - R \sin θ {(\frac{d θ}{d t})}^{2} \\ \frac{d V_{y}}{d t} = R \frac{d^{2} θ}{d t} \sin θ + R cos θ {(\frac{d θ}{d t})}^{2} \end{array}$

Volvemos a la ecuación del movimiento, y sustituimos las derivadas de las componentes de la velocidad del c.m. del bloque por sus expresiones en términos del ángulo θ y sus derivadas respecto del tiempo. Haciendo algunas operaciones se llega a la siguiente ecuación diferencial de segundo orden.

$(m \cdot \sin^{2} θ + M) R \frac{d^{2} θ}{d t^{2}} = F \cos θ - \frac{m R \cdot \sin 2 θ}{2} {(\frac{d θ}{d t})}^{2} - (m + M) g \cdot \sin θ$

Dado el valor de la fuerza interna F, resolvemos esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales t=0, θ=0, dθ/dt=0.

Final del choque

Se finaliza el choque, en el instante t_c tal que la componente a lo largo del eje X de la velocidad del c.m. V_x=V_c·cosθ_c coincide con la componente X de la velocidad de la bala

$\begin{array}{l} v_{x} = v_{0} - \frac{F}{m} t_{c} \\ V_{c} \cos θ_{c} = v_{0} - \frac{F}{m} t_{c} \end{array}$

Donde θ_c es el desplazamiento angular del c.m. del bloque en el instante t_c y V_c la velocidad del c.m. del bloque en dicho instante.

Ya hemos mencionado que las componentes Y coinciden en todo momento V_y=v_y.

Movimiento después del choque

Una vez que ha finalizado el choque, el bloque y la bala se mueven como un solo cuerpo de masa (m+M) bajo la acción de su peso y de la tensión de las cuerdas. El c.m. del sistema se mueve de acuerdo con la ecuación diferencial deducida en el primer apartado.

$\frac{d^{2} θ}{d t^{2}} + \frac{g}{R} \sin θ = 0$

con las condiciones iniciales t=0, θ= θ_c, dθ/dt=V_c/R.

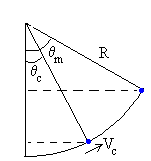
Conocida la velocidad V_c y el desplazamiento angular θ_c, del sistema formado por el bloque y la bala en el instante t_c en el que termina el choque, podemos determinar sin resolver la ecuación diferencial el máximo desplazamiento θ_m, aplicando el principio de conservación de la energía.

$\begin{array}{l} \frac{1}{2} (m + M) V_{c}^{2} = (m + M) g (R \cos θ_{c} - R \cos θ_{m}) \\ \cos θ_{m} = \cos θ_{c} - \frac{V_{c}^{2}}{2 g R} \end{array}$

Cálculo con MATLAB

Resolvemos las ecuaciones diferenciales que describen las dos etapas en el movimiento del bloque para el siguiente caso:

La longitud de las varillas que sujetan el bloque, R=1 m
La masa del bloque, M=1 kg
La masa de la bala, m=0.4 kg
La velocidad inicial de la bala, v₀=10 m/s
La fuerza de interacción entre el bloque y la bala, F=20 N

Primera etapa del movimiento

Creamos una función stop_balistico que detiene el proceso de integración cuando la velocidad de la bala se iguala a la componente horizontal de la velocidad del c.m. bloque

function [value,isterminal,direction]=stop_balistico(t,x, v0, F, m, R)
   %x(1) es  x, x(2) es v
    vBala=v0-F*t/m; %velocidad de la bala
    vX=R*x(2)*cos(x(1)); %componente X de la velocidad del bloque
    value=vX-vBala;
    isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
    direction=0; % 1 crece, -1 decrece, 0 no importa
end

Resolvemos la ecuación diferencial del movimiento del bloque, hasta que la bala se detiene en el interior del bloque con las condiciones iniciales siguientes: en el instante t=0, θ=0, dθ/dt=0. Parte del reposo

R=1; %radio
M=1; %masa bloque
m=0.4; %masa bala
v0=10; %velcidad inicial dela bala
F=20; %fuerza de rozamiento

hold on
opts=odeset('events',@(t,x) stop_balistico(t,x, v0, F, m, R));
f=@(t,x) [x(2);(F*cos(x(1))-m*R*x(2)^2*sin(2*x(1))/2-(m+M)*9.8*sin(x(1)))
/(R*(m*sin(x(1))^2+M))]; 
[t,x]=ode45(f,[0,2],[0,0], opts);
plot(t,x(:,1))
line([t(end),t(end)],[0,x(end,1)],'lineStyle','--','color','k')
line([0,t(end)],[x(end,1),x(end,1)],'lineStyle','--','color','k')
....

El tiempo, t_c, el desplzamiento angular θ_c y velocidad del c.m. del bloque al finalizar la primera etapa son

>> t(end)
ans =    0.1463
>> x(end,1)*180/pi
ans =   11.9064
>> x(end,2)
ans =    2.7447

Segunda etapa del movimiento

Creamos una función stop_pendulo que detiene el proceso de integración cuando el bloque alcanza el máximo desplazamiento angular, es decir, su velocidad angular es nula, dθ/dt=0

function [value,isterminal,direction]=stop_pendulo(t,x)
     value=x(2);
    isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
    direction=-1; % 1 crece, -1 decrece, 0 no importa
end

Resolvemos la ecuación diferencial del movimiento del bloque, desde que la bala se detiene en el interior del bloque con las condiciones iniciales siguientes: en el instante t=t_c, θ=θ_c, dθ/dt=(dθ/dt)_c. Es decir, las finales de la etapa anterior

Añadimos al script anterior, las siguientes líneas de código

....
opts=odeset('events',@stop_pendulo);
f=@(t,x) [x(2);-9.8*sin(x(1))/R]; 
[t,x]=ode45(f,[t(end),2],[x(end,1),x(end,2)], opts);
plot(t,x(:,1))
line([t(end),t(end)],[0,x(end,1)],'lineStyle','--','color','k')
line([0,t(end)],[x(end,1),x(end,1)],'lineStyle','--','color','k')

hold off
grid on
xlabel('t')
ylabel('x');
title('Choque de duración finita')

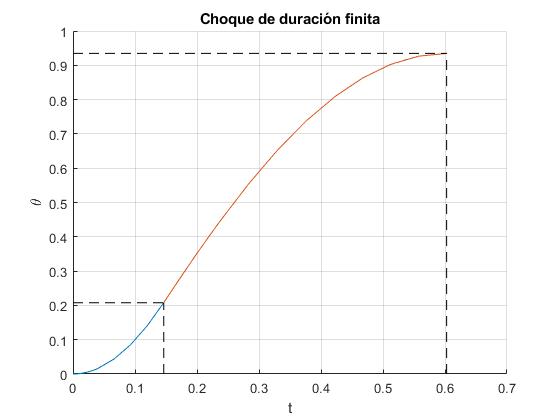
El tiempo que tarda en alcanzar el máximo desplazamiento y el desplazamiento al finalizar la segunda etapa, son

>> t(end)
ans =    0.6025
>> x(end,1)*180/pi
ans =   53.5484

Velocidades

Representamos la velocidad de la bala y la componente horizontal de la velocidad del c.m., que coinciden al finalizar la primera etapa del movimiento

R=1; %radio
M=1; %masa bloque
m=0.4; %masa bala
v0=10; %velcidad inicial dela bala
F=20; %fuerza de rozamiento

hold on
opts=odeset('events',@(t,x) stop_balistico(t,x, v0, F, m, R));
f=@(t,x) [x(2);(F*cos(x(1))-m*R*x(2)^2*sin(2*x(1))/2-(m+M)*9.8*sin(x(1)))
/(R*(m*sin(x(1))^2+M))]; 
[t,x]=ode45(f,[0,2],[0,0], opts);
plot(t,R*x(:,2).*cos(x(:,1)))
vBala=v0-F*t/m;
plot(t,vBala)
line([t(end),t(end)],[0,vBala(end)],'lineStyle','--','color','k')
line([0,t(end)],[vBala(end),vBala(end)],'lineStyle','--','color','k')

hold off
grid on
legend('bloque','bala')
xlabel('t')
ylabel('v');
title('Choque de duración finita')

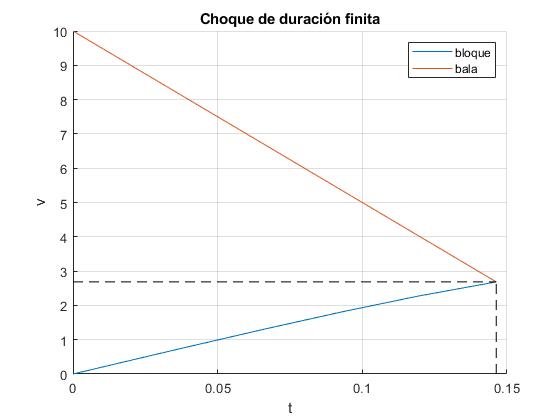
La velocidad final de la bala respecto al bloque es nula, respecto al laboratorio es

>> vBala(end)
ans =    2.6857
>> R*x(end,2)*cos(x(end,1))
ans =    2.6857

En la figura, se representa el desplazamiento angular del bloque para tres valores de la fuerza F de interacción entre el bloque y la bala: 15, 30 y 45 N

R=1; %radio
M=1; %masa bloque
m=0.4; %masa bala
v0=10; %velcidad inicial dela bala
color=['r','b','k'];
hold on
i=1;
for F=[15, 30,45] %fuerza de rozamiento
    opts=odeset('events',@(t,x) stop_balistico(t,x, v0, F, m, R));
    f=@(t,x) [x(2);(F*cos(x(1))-m*R*x(2)^2*sin(2*x(1))/2-(m+M)*9.8*sin(x(1)))
/(R*(m*sin(x(1))^2+M))]; 
    [t,x]=ode45(f,[0,2],[0,0], opts);
    plot(t,x(:,1), color(i))
    opts=odeset('events',@stop_pendulo);
    f=@(t,x) [x(2);-9.8*sin(x(1))/R]; 
    [t,x]=ode45(f,[t(end),2],[x(end,1),x(end,2)], opts);
    plot(t,x(:,1),color(i))
    line([0,t(end)],[x(end,1),x(end,1)],'lineStyle','--','color','k')
    i=i+1;
end
hold off
grid on
xlabel('t')
ylabel('\theta');
title('Choque de duración finita')

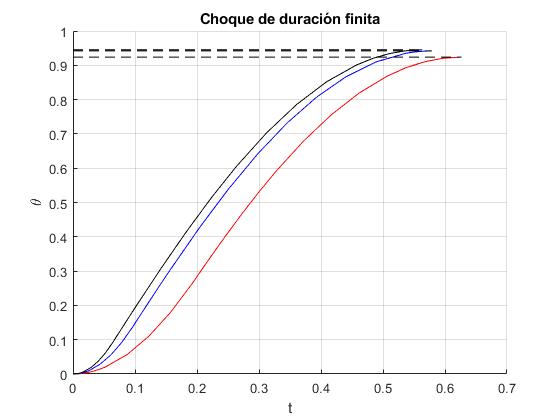
Cuando la fuerza F es grande, apenas hay diferencias en el ángulo final. Cuando la fuerza F es pequeña, ya hay más diferencias, pero el bloque ha de ser muy largo para que la bala no salga por el extremo derecho, sin deternerse dentro del bloque. Esta situación no se contempla en la el programa interactivo al final de la página, pero si se contempla en la otra página que describe el choque inelástico de duración finita

Conclusiones

Se ha descrito un choque inelástico entre una bala y un bloque. En el caso de que el choque sea instantáneo, se puede aplicar el principio de conservación del momento lineal, ya que las fuerzas exteriores que actúan sobre el sistema se anulan. En el caso de que el choque sea de duración finita, las fuerzas exteriores que actúan sobre el sistema de partículas no se anulan durante el intervalo de tiempo que dura el choque, por lo que no se puede aplicar el principio de conservación del momento lineal.

Se deberá esperar que cuanto más corta sea la duración del choque, es decir, más grande sea la fuerza interna F de frenado que ejerce el bloque sobre la bala, los resultados de las dos descripciones serán cada vez más parecidos. En el límite, cuando F tiene a infinito, tendremos un choque instantáneo, y obtendremos los resultados que predice el principio de conservación del momento lineal.

El programa interactivo, resuelve las ecuaciones del movimiento empleando procedimientos numéricos. Además de las imprecisiones propias de los procedimientos numéricos hay que añadir una dificultad más en la resolución de las ecuaciones del movimiento. Cuanto mayor sea la fuerza F, más corta es la duración del choque, el paso de integración se ha de hacer más pequeño para que los resultados sean fiables.

Actividades

Se introduce

La masa m de la bala en kg, en el control titulado Masa bala
La velocidad v₀ de la bala en m/s, en el control titulado Velocidad bala
La fuerza F en newton de interacción entre el bloque y la bala, en el control titulado Fuerza.
La masa del bloque está fijada en el valor M=1kg
La longitud del bloque se ha fijado en el valor L=1 m
La longitud de las varillas que sujetan el bloque se ha fijado en R=1 m

Se pulsa el botón titulado Nuevo

Se mueve la bala, un pequeño círculo de color rojo, hacia una de las caras del bloque. Cuando la bala toca al bloque, se observa:

El movimiento de la bala penetrando en el bloque
La fuerza interna F que actúa sobre la bala, y sobre el c.m. del bloque.

En la parte derecha, se proporcionan los siguientes datos:

El tiempo medido desde el momento en que la bala entra en contacto con el bloque
El desplazamiento angular θ del c.m. del bloque (ángulo que forman las dos varillas con la vertical)
La velocidad V del c.m. del bloque
La componente X velocidad de la bala v_x=v₀-F·t/m
La componente X velocidad del bloque V_x=V·cos θ

Observaremos que la componente X de la velocidad de la bala, disminuye y aumenta la componente X de la velocidad del bloque. Emplearemos la combinación de botones || y >|, para acercarnos al momento en el que termina el choque cuando ambas velocidades (en color rojo) toman el mismo valor. Anotaremos

el tiempo t_c
la desviación θ_c del bloque.
la velocidad del bloque V_c.

Comparamos la velocidad V_c con la velocidad v_f que se obtiene de la aplicación del principio de conservación del momento lineal (choque instantáneo)

$v_{f} = \frac{m}{m + M} v_{0}$

Pulsamos el botón titulado ►, para que el sistema prosiga su movimiento hasta alcanzar el máximo desplazamiento.

Nos fijamos que la bala y el bloque se mueven con la misma velocidad (en color rojo)

El programa se detiene cuando el sistema formado por el bloque y la bala alcanza el máximo desplazamiento, la velocidad V se hace cero (en color azul). Se sugiere al lector comparar los máximos desplazamientos que se obtienen mediante el modelo de choque instantáneo y mediante el modelo de choque de duración finita.

Ejemplo:

Introducimos los siguientes valores:

Masa de la bala m=0.4 kg
Velocidad de la bala v₀=10 m/s
Fuerza de interacción F=20 N

Se pulsa el botón titulado Nuevo

Choque instantáneo

Aplicando el principio de conservación del momento lineal, obtenemos la velocidad del conjunto bloque-bala después del choque

0.4·10=(1+0.4)·v_f v_f=2.86 m/s

Aplicando el principio de conservación de la energía, obtenemos el ángulo máximo que se desvía el péndulo balístico después del choque

$\sin (\frac{θ_{m}}{2}) = \frac{v_{f}}{2 \sqrt{g R}} θ_{m} = 2 \cdot \arcsin (\frac{2.86}{2 \sqrt{9.8 \cdot 1.0}}) = 54.3 º$

Choque de duración finita

Observamos los valores de las componentes X de las velocidades de la bala v_x y del bloque V_x (en color rojo) Cuando estas componentes son iguales el choque finaliza, las flechas que señalan la fuerza interna F que disminuye la velocidad de la bala y aumenta la del bloque, desparecen.

El choque transcurre durante un tiempo t_c=0.147 s.
La velocidad del bloque en este instante es V_c=2.75 m/s
El ángulo que se ha desviado las varillas de la vertical es θ_c=11.92º.

Después del choque t>t_c las velocidades de la bala y del bloque son las mismas.

Aplicando el principio de conservación de la energía, podemos calcular la máxima desviación θ_m del conjunto formado por el bloque y la bala después del choque.

$\cos θ_{m} = \cos 11.92 - \frac{{2.75}^{2}}{2 \cdot 9.8 \cdot 1.0} θ_{m} = 53.66 º$

Ejemplo 2

Masa de la bala m=0.4 kg
Velocidad de la bala v₀=10 m/s
Fuerza de interacción F=90 N

Se obtienen los siguientes resultados

La duración del choque disminuye a t_c=0.032 s.
El desplazamiento del bloque es pequeño θ_c=2.6º
El conjunto bloque-bala alcanza una velocidad de V_c=2.85 m/s. muy parecida a la que se obtiene aplicando el principio de conservación del momento lineal.
La desviación máxima que alcanza después del choque es θ_m=54.3º, un valor similar al calculado empleando la aproximación de choque instantáneo.

Masa bala (kg): Velocidad bala (m/s)
Fuerza

Referencias

Donnelly D, Diamond J. Slow collisions in the ballistic pendulum: A computational study. Am. J. Phys. 71 (6) June 2003, pp. 535-540.