Por ejemplo, un vehículo dispone de un motor que entrega una potencia cuando su motor gira a una determinada rpm (revoluciones por minuto), la fuerza de rozamiento entre las ruedas y el suelo es el mecanismo que disipa la energía cuando su velocidad es pequeña, a medida que incrementa su velocidad, el rozamiento con el aire, dependiente de la velocidad es el principal mecanismo de disipación. El vehículo alcanza una velocidad final constante. Una descripción similar se puede aplicar al movimiento de los organismos vivos.

Supondremos que el vehículo describe un movimiento rectilíneo a lo largo del eje , parte de la posición x₀ con velocidad v₀ en el instante t=0

Sin rozamiento

Consideremos el caso más simple, el vehículo de masa m, cuyo motor entrega una potencia contante P, se mueve en un medio que no disipa energía. Vamos a obtener las ecuaciones del movimiento, sabiendo que el vehículo parte de la posición inicial x₀, con velocidad inicial v₀ en el instante t=0.

La potencia P es el producto escalar

${\displaystyle P=\frac{dW}{dt}=\frac{\overrightarrow{F}·\overrightarrow{dr}}{dt}=\overrightarrow{F}·\overrightarrow{v}}$

Para un movimiento rectilíneo, P=F·v, la segunda ley de Newton se escribe, F=ma=mdv/dt. La ecuación diferencial del movimiento es

${\displaystyle m\frac{dv}{dt}=\frac{P}{v}}$

Velocidad

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}v·dv=}{\displaystyle \underset{0}{\overset{t}{\int }}P·dt}\\ \frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2=Pt\\ v=\sqrt{2\left(\frac{P}{m}\right)t+v_0^2}=\sqrt{2Z^{2}t+v_0^2}=Z\sqrt{2t+\frac{v_0^2}{Z^2}},Z=\sqrt{\frac{P}{m}}\end{array}}$

Cuando la fuerza aplicada F es constante, el movimiento rectilíneo es uniformente aceelrado y la velocidad del vehículo en el instante t es

${\displaystyle v=v_0+\frac{F}{m}t}$

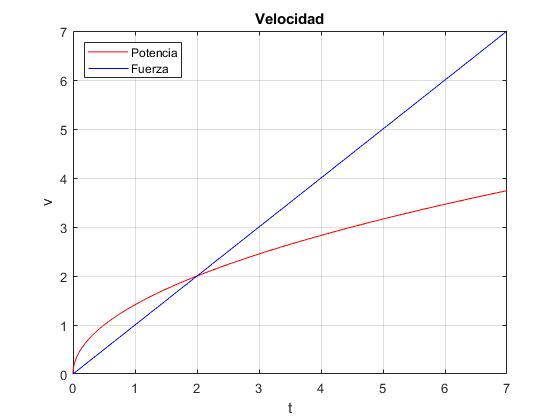
Supongamos que el cuerpo parte del reposo, v₀=0, en el instante t=0. Sea F/m=P/m=1. Comparamos las dos expresiones de la velocidad v:

• Potencia constante
• Fuerza constante

tFin=7;
fplot(@(t) sqrt(2*t),[0,tFin],'color','r')
line([0,tFin],[0,tFin], 'color','b')
xlabel('t')
ylabel('v')
legend('Potencia','Fuerza', 'Location','northwest')
grid on
title('Velocidad')

Aceleración y posición

Derivando con respecto del tiempo t, obtenemos la aceleración a

${\displaystyle a=\frac{dv}{dt}=\frac{Z}{\sqrt{2t+\frac{v_0^2}{Z^2}}}}$

Como v=dx/dt, integrando, obtenemos la posición x del móvil en el instante t

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0}{\overset{x}{\int }}dx}={\displaystyle \underset{0}{\overset{t}{\int }}Z\sqrt{2t+\frac{v_0^2}{Z^2}}·dt}\\ x=x_0+\frac{Z}{3}\left\{{\left(2t+\frac{v_0^2}{Z^2}\right)}^{3/2}-\frac{v_0^3}{Z^3}\right\}=x_0+\frac{Z}{3}\left\{\frac{v^3}{Z^3}-\frac{v_0^3}{Z^3}\right\}\end{array}}$

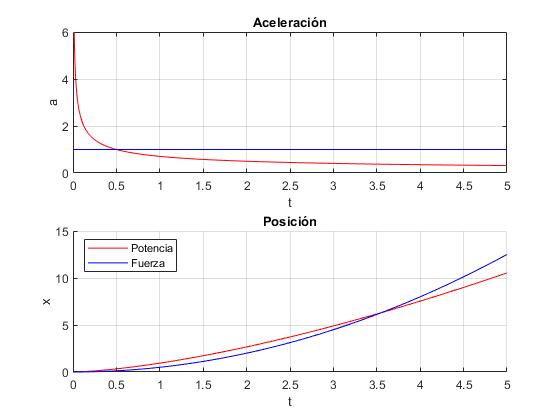
Cuando el móvil parte del origen x₀=0, en reposo v₀=0 en el instante t=0. Comparamos las ecuaciones del movimiento de un vehículo cuyo motor entrega una potencia constante P (a la izquierda) con un vehículo que se mueve bajo la acción de una fuerza constante F (a la derecha)

${\displaystyle \{\begin{array}{l}a=\frac{P}{m}\frac{1}{\sqrt{2t}}\\ v=\frac{P}{m}\sqrt{2t}\\ x=\frac{1}{3}\frac{P}{m}{\left(2t\right)}^{3/2}\end{array}\{\begin{array}{l}a=\frac{F}{m}\\ v=\frac{F}{m}t\\ x=\frac{1}{2}\frac{F}{m}{t}^2\end{array}}$

Representamos la aceleración a y la posición x del vehículo en función del tiempo t, para F/m=P/m=1

tFin=5;
subplot(2,1,1)
fplot(@(t) 1./sqrt(2*t),[0,tFin], 'color','r')
line([0,tFin],[1,1], 'color','b')
ylim([0,6])
xlabel('t')
ylabel('a')
grid on
title('Aceleración')

subplot(2,1,2)
hold on
fplot(@(t) ((2*t).^(3/2))/3,[0,tFin],'color','r')
fplot(@(t) t.^2/2,[0,tFin], 'color','b')
hold off
legend('Potencia','Fuerza', 'Location','northwest')
xlabel('t')
ylabel('x')
grid on
title('Posición')

Movimiento en un medio disipativo

Dos fuerzas actúan sobre el móvil: la fuerza F=P/v que hace que el vehículo se mueva y la fuerza de rozamiento F_r, que se opone al movimiento y por tanto, opuesta a F. La ecuación del movimiento, se escribe

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=\frac{P}{v}-F_r\\ \frac{dv}{dt}=\frac{Z}{v}-f\end{array}}$

Dada la fuerza de rozamiento F_r o f=F_r/m, obtendremos la aceleración a=dv/dt y la velocidad v=dx/dt, con el dato de la velocidad inicial v₀ en el instante t=0. Examinaremos tres casos

Desde el punto de vista energético, podemos describir el movimiento del siguiente modo:

P es la energía por unidad de tiempo que entrega el motor, que se convierte una parte en energía cinética y otra parte, se disipa en forma del calor.

${\displaystyle \begin{array}{l}P=\frac{d{E}_k}{dt}+\frac{dQ}{dt}\\ P=\frac{d}{dt}\left(\frac{1}{2}m{v}^2\right)+\frac{F_{r}dx}{dt}\\ P=mv\frac{dv}{dt}+F_{r}v\end{array}}$

Donde dW=-F_rdx es el trabajo realizado por la fuerza de rozamiento, F_r de sentido contrario al desplazamiento, dx

Cuando se suministra una potencia constante a una vehículo, ocurren dos procesos:

1. Se incrementa la energía cinética del vehículo al aumentar la velocidad
2. Se pierde energía en forma de calor debido al trabajo de las fuerzas de rozamiento

A medida que la velocidad se incrementa, también lo hace la energía disipada. Al cabo de un cierto tiempo, la energía por unidad de tiempo suministrada al vehículo P se va igualando a la energía disipada, la velocidad se hace casi constante, independientemente del tipo de proceso disipativo, como vamos a ver en los siguientes ejemplos

Fuerza de rozamiento constante

En este caso, f es constante

Integrando la ecuación del movimiento, obtenemos la velocidad

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{\frac{Z}{v}-f}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Sustituyendo u=Z-fv, du=-f·dv

${\displaystyle {\displaystyle \int \frac{vdv}{Z-fv}}=-\frac{1}{f^2}{\displaystyle \int \left(\frac{Z}{u}-1\right)}du=-\frac{1}{f^2}\left(Z\ln u-u\right)=-\frac{1}{f^2}\left(Z\ln \left(Z-fv\right)-Z+fv\right)}$

El resultado es

${\displaystyle \begin{array}{l}\frac{Z}{f^2}\ln \frac{Z-f{v}_0}{Z-fv}+\frac{1}{f}\left(v_0-v\right)=t\\ \alpha \ln \frac{\alpha -v_0}{\alpha -v}+\left(v_0-v\right)=f·t,\alpha =\frac{Z}{f}\end{array}}$

Representamos la velocidad v en función del tiempo t para α=Z/f=0.8, y para dos valores de la velocidad inicial v₀

alfa=0.8;
hold on
for v0=[0,1.5]
    f=@(t,v) log((alfa-v0)./(alfa-v))+v0-v-t;
    fimplicit(f,[0,5,0,2])
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Fuerza de rozamiento constante')

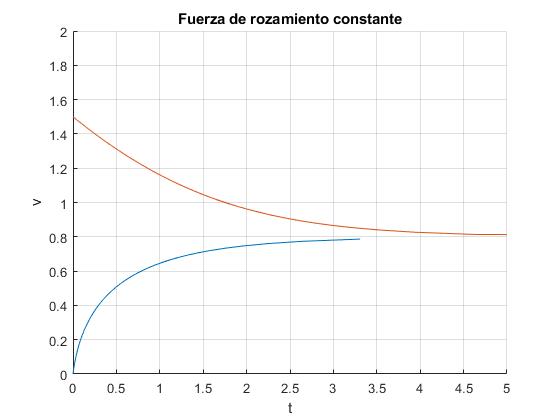
La velocidad tiende hacia el valor constante α=Z/f

Fuerza de rozamiento proporcional a la velocidad

En este caso, f=kv

Integrando la ecuación del movimiento, obtenemos la velocidad

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{\frac{Z}{v}-kv}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Se hace el cambio de variable, u=kv²-Z

${\displaystyle -{\displaystyle \int \frac{vdv}{k{v}^2-Z}}=-\frac{1}{2k}{\displaystyle \int \frac{du}{u}}=-\frac{1}{2k}\ln u=-\frac{1}{2k}\ln \left(k{v}^2-Z\right)}$

El resultado es

${\displaystyle \begin{array}{l}\ln \frac{k{v}^2-Z}{k{v}_0^2-Z}=-2kt\\ v^2=\frac{Z}{k}+\left(v_0^2-\frac{Z}{k}\right)\exp \left(-2kt\right)\\ v^2=\alpha +\left(v_0^2-\alpha \right)\exp \left(-2kt\right),\alpha =\frac{Z}{k}\end{array}}$

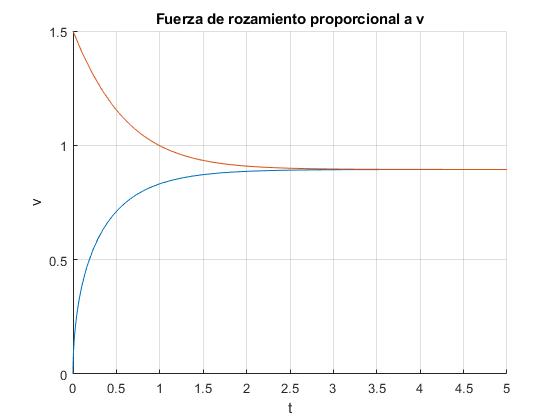
La velocidad final tiende a

${\displaystyle v_{\infty }=\sqrt{\alpha }=\sqrt{\frac{Z}{k}}}$

Representamos la velocidad v en función del tiempo t para α=Z/k=0.8, para dos valores de la velocidad inicial v₀

alfa=0.8;
hold on
for v0=[0,1.5]
    f=@(t) sqrt(alfa+(v0^2-alfa)*exp(-2*t));
    fplot(f,[0,5])
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Fuerza de rozamiento proporcional a v')

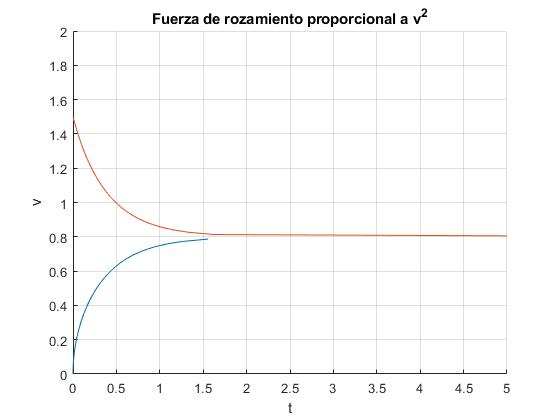
Fuerza de rozamiento proporcional al cuadrado de la velocidad

En este caso, f=kv²

Integrando la ecuación del movimiento, obtenemos la velocidad

${\displaystyle {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{\frac{Z}{v}-k{v}^2}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

El integrando se divide en fracciones simples,

${\displaystyle \begin{array}{l}-{\displaystyle \int \frac{vdv}{k{v}^3-Z}}=-\frac{1}{k}{\displaystyle \int \frac{vdv}{v^3-{\alpha }^3}},{\alpha }^3=\frac{Z}{k}\\ \frac{v}{v^3-{\alpha }^3}=\frac{v}{\left(v-\alpha \right)\left(v^2+\alpha v+{\alpha }^2\right)}=\frac{A}{v-\alpha }+\frac{Bv+C}{v^2+\alpha v+{\alpha }^2}\{\begin{array}{l}A=\frac{1}{3\alpha }\\ B=-\frac{1}{3\alpha }\\ C=\frac{1}{3}\end{array}\\ -\frac{1}{k}{\displaystyle \int \frac{vdv}{v^3-{\alpha }^3}}=-\frac{1}{k}\left\{\frac{1}{3\alpha }\ln \left(v-\alpha \right)+\frac{1}{3\alpha }{\displaystyle \int \frac{\alpha -v}{v^2+\alpha v+{\alpha }^2}dv}\right\}\end{array}}$

Se resuelve la integral

${\displaystyle {\displaystyle \int \frac{\alpha -v}{v^2+\alpha v+{\alpha }^2}dv}={\displaystyle \int \frac{\alpha -v}{{\left(v+\frac{\alpha }{2}\right)}^2+\frac{3}{4}{\alpha }^2}dv}}$

Haciendo el cambio de variable u=v+α/2

${\displaystyle {\displaystyle \int \frac{\frac{3}{2}\alpha -u}{u^2+\frac{3}{4}{\alpha }^2}du}=\frac{3}{2}\alpha {\displaystyle \int \frac{du}{u^2+\frac{3}{4}{\alpha }^2}-}{\displaystyle \int \frac{u}{u^2+\frac{3}{4}{\alpha }^2}du}}$

En la primera integral hacemos el cambio $u=\frac{\sqrt{3}}{2}\alpha \tan \theta$, la segunda es inmediata

${\displaystyle \sqrt{3}\arctan \left(\frac{2u}{\sqrt{3}\alpha }\right)-\frac{1}{2}\ln \left(u^2+\frac{3}{4}{\alpha }^2\right)}$

El resultado es

${\displaystyle -\frac{1}{3k\alpha }\left\{\ln \left(v-\alpha \right)+\sqrt{3}\arctan \left(\frac{2v+\alpha }{\sqrt{3}\alpha }\right)-\frac{1}{2}\ln \left(v^2+\alpha v+{\alpha }^2\right)\right\}}$

Evaluamos los límites de la integral

${\displaystyle \begin{array}{l}-\frac{1}{3\alpha }{\left\{\ln \left(v-\alpha \right)+\sqrt{3}\arctan \left(\frac{2v+\alpha }{\sqrt{3}\alpha }\right)-\frac{1}{2}\ln \left(v^2+\alpha v+{\alpha }^2\right)\right\}}_{v_0}^v=kt\\ \frac{1}{\alpha }\left\{\frac{1}{3}\ln \left(\frac{v_0-\alpha }{v-\alpha }\sqrt{\frac{v^2+\alpha v+{\alpha }^2}{v_0^2+\alpha v_0+{\alpha }^2}}\right)+\frac{1}{\sqrt{3}}\arctan \left(\frac{2v_0+\alpha }{\sqrt{3}\alpha }\right)-\frac{1}{\sqrt{3}}\arctan \left(\frac{2v+\alpha }{\sqrt{3}\alpha }\right)\right\}=kt,{\alpha }^3=\frac{Z}{k}\end{array}}$

Representamos la velocidad v en función del tiempo t para α=Z/k=0.8, para dos valores de la velocidad inicial v₀

alfa=0.8;
hold on
for v0=[0,1.5]
    f=@(t,v) log(((alfa-v0)*sqrt(v.^2+alfa*v+alfa^2))./((alfa-v)*
sqrt(v0^2+alfa*v0+alfa^2)))/3+atan((2*v0+alfa)/(sqrt(3)*alfa))
/sqrt(3)-atan((2*v+alfa)/(sqrt(3)*alfa))/sqrt(3)-alfa*t;
    fimplicit(f,[0,5,0,2])
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Fuerza de rozamiento proporcional a v^2')

Referencias

José M Pérez Ramos, Carmen Toro Castillo, Héctor O González Ochoa. Constant power dissipative motion. Eur. J. Phys. 41 (2020) 045004

Roger Stephenson. Constant power equations of motion. Am. J. Phys. 50 (12) Dec. 1982. pp. 1150-1155