En la página titulada la catenaria hemos deducido la ecuación de esta famosa curva que describe la forma que adopta un cable suspendido de los extremos de dos postes iguales. La ecuación de una catenaria en forma de cúpula con el eje Y de simetría es

${\displaystyle y=\frac{1}{2\gamma }\left(\cosh (\gamma a)-\cosh (2\gamma x)\right)}$

Representamos esta catenaria de longitud L, cuyos extremos están fijos en los puntos (-a/2,0) y (a/2,0). El parámetro γ se calcula a partir de la longitud L del cable y de la 'luz' (distancia entre extremos) a, tal como vemos en el siguiente script de MATLAB

L=1; %longitud de la catenaria
a=0.5; %'luz'
f=@(x) sinh(a*x)-L*x;
gamma=fzero(f,[0.1 100]);
f=@(x) (cosh(gamma*a)-cosh(2*gamma*x))/(2*gamma);
fplot(f,[-a/2,a/2]);
grid on
xlabel('x');
ylabel('y');
title('Catenaria')

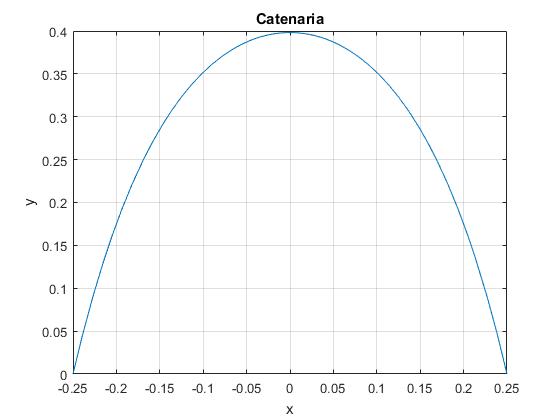
Para este problema conviene establecer la ecuación de la trayectoria en forma paramétrica, tal como se hizo para la cúpula en forma de cicloide.

Llamamos 2γ=1/R, x=R·φ

y=R(cosh(γa)-cosh(φ))

Para φ=0, y=R por lo que cosh(γa)=2,

El valor mayor de φ se obtiene con a/2=Rφ₀, , cosh(φ₀)=2, φ₀=1.317

>> acosh(2)
ans =    1.3170

Las ecuaciones paramétricas de la catenaria son

x=Rφ
y=R(2-cosh(φ))

Donde R y φ son dos parámetros

Cuando φ=0, x=0, y=R, es el vértice de la catenaria, cuando φ=φ₀, x=R·φ₀, y=0 es el extremo de la catenaria, tal como se ve en la figura

R=1;
fplot(@(x) R*x,@(x) R*(2-cosh(x)),[0,acosh(2)]);
grid on
xlabel('x');
ylabel('y');
title('Catenaria')

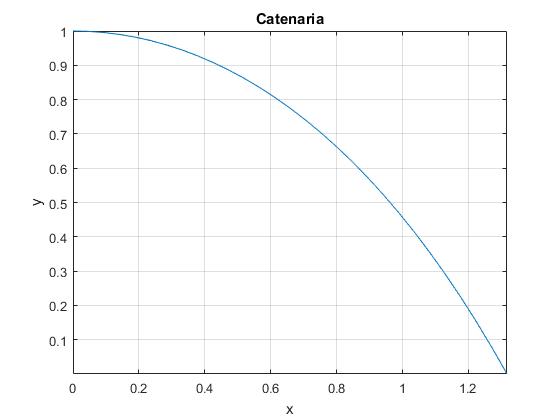
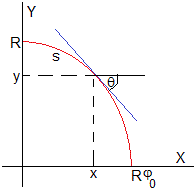
La pendiente de la recta tangente a la curva en la posición (x, y), tal como vemos en la figura.

${\displaystyle \tan \theta =\frac{dy}{dx}=\frac{-R\sinh \phi ·d\phi }{R\text{·}d\phi }=-\sinh \phi }$

Omitimos el signo y relacionamos el parámetro φ y el ángulo (positivo) de la pendiente, sinhφ=tanθ

En el vértice φ=0, la pendiente θ=0. En el extremo, φ₀=arccosh(2), tanθ₀=$\sqrt{3}$, θ₀=1.0472

Calculamos la longitud del arco s, entre el vértice y el punto de coordenadas (x, y)

${\displaystyle \begin{array}{l}d{s}^2=d{x}^2+d{y}^2=\left(R^2+R^2{\sinh }^2\phi \right){\left(d\phi \right)}^2=R^2{\cosh }^2\phi ·{\left(d\phi \right)}^2\\ ds=R\cosh \phi ·d\phi \\ s={\displaystyle \underset{0}{\overset{\phi }{\int }}R\cosh \phi ·d\phi =R\sinh \phi =R\tan \theta }\\ ds=\frac{R}{{\cos }^2\theta }d\theta \end{array}}$

El radio de curvatura ρ de la cicloide en la posición (x, y) se calcula mediante la fórmula

${\displaystyle \rho =\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{x}^2}\right|}}$

Calculamos la derivada primera dy/dx y segunda d²y/dx²

${\displaystyle \begin{array}{l}\frac{dy}{dx}=-\sinh \phi \\ \frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d}{d\phi }\left(\frac{dy}{dx}\right)\frac{1}{\frac{dx}{d\phi }}=-\frac{\cosh \phi }{R}\end{array}}$

El resultado es

${\displaystyle \rho =\frac{{\left(1+{\sinh }^2\phi \right)}^{3/2}}{\frac{\cosh \phi }{R}}=R{\cosh }^2\phi =R\left(1+{\tan }^2\theta \right)=\frac{R}{{\cos }^2\theta }}$

El mismo resultado se obtiene a partir de la definición de radio de curvatura, ds=ρ·dθ

${\displaystyle \rho =\frac{ds}{d\theta }=\frac{R}{{\cos }^2\theta }}$

El radio de curvatura ρ es una cantidad positiva.

Dibujamos el arco de catenaria en el intervalo 0≤φ≤arccosh(2), calculamos la expresión del radio de curvatura, dibujamos la tangente y la normal a la catenaria en el punto correspondiente al parámetro φ=arccosh(2)/2. El extremo de la normal es el centro de curvatura (no se ve en la figura), pero puede verse desplazando la gráfica mediante la herramienta 'Pan'

syms phi xx;
R=1;
x=R*phi;
y=R*(2-cosh(phi));
yp=diff(y,phi)/diff(x,phi);
ypp=diff(yp,phi)/diff(x,phi);
r=(1+yp^2)^(3/2)/ypp;
hold on
ezplot(x,y,[0,acosh(2)])
grid on
x1=double(subs(x,phi,acosh(2)/2));
y1=double(subs(y,phi,acosh(2)/2));
rho=double(subs(r,phi,acosh(2)/2));
m1=double(subs(yp,phi,acosh(2)/2)); %pendiente tangente
m2=-1/m1; %pendiente normal
xc=x1+rho/sqrt(m2^2+1); %centro de curvatura
yc=y1+m2*(xc-x1);
y=m2*xx+y1-m2*x1;
ezplot(y,[xc,x1]) %normal
y=m1*xx+y1-m1*x1;
ezplot(y,[x1-0.5,x1+0.5]) %tangente

axis equal
xlim([0,acosh(2)])
ylim([0,1])
hold off
xlabel('x')
ylabel('y')
title('Catenaria')

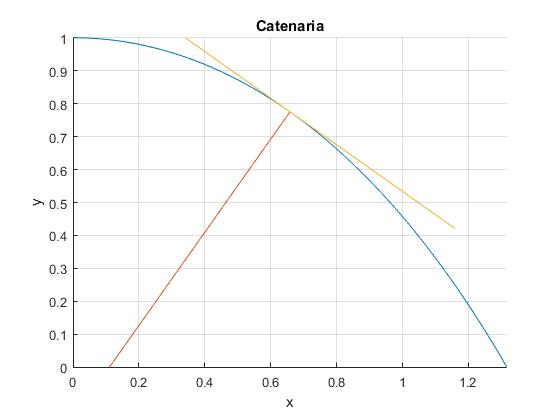
Ecuación del movimiento

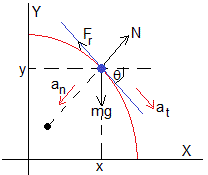
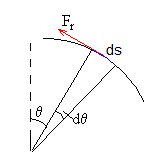
Dibujamos las fuerzas que actúan sobre la partícula, cuando se encuentra en la posición (x, y).

• El peso mg
• La reacción N de la cúpula
• La fuerza de rozamiento F_r=μN

La partícula describe un movimiento con aceleración tangencial a_t y aceleración normal a_n. Aplicando la segunda ley de Newton

• Ecuación del movimiento en la dirección tangencial

mg·sinθ-F_r=ma_t

• Ecuación del movimiento en la dirección normal

mg·cosθ-N=ma_n

Teniendo en cuenta las definiciones de aceleración tangencial a_t y aceleración normal a_n,

${\displaystyle a_t=\frac{dv}{dt}{a}_n=\frac{v^2}{\rho }}$

Eliminando la reacción N de la superficie en el punto de contacto, expresamos las dos ecuaciones del movimiento en una única ecuación diferencial

${\displaystyle \frac{dv}{dt}=g\sin \theta -\mu g\cos \theta +\mu \frac{v^2}{\rho }}$

La velocidad v y la aceleración dv/dt se expresan en términos del parámetro θ, (el ángulo de la recta tangente a la trayectoria) y sus derivadas respecto del tiempo.

${\displaystyle \begin{array}{l}v=\frac{ds}{dt}=\frac{R}{{\cos }^2\theta }\frac{d\theta }{dt}\\ \frac{dv}{dt}=\frac{2R\sin \theta }{{\cos }^3\theta }{\left(\frac{d\theta }{dt}\right)}^2+\frac{R}{{\cos }^2\theta }\frac{d^2\theta }{d{t}^2}\end{array}}$

Se obtiene la ecuación diferencial de segundo orden

${\displaystyle \frac{d^2\theta }{d{t}^2}+\left(2\tan \theta -\mu \right){\left(\frac{d\theta }{dt}\right)}^2-\frac{g}{R}\left(\sin \theta -\mu \cos \theta \right){\cos }^2\theta =0}$

que se resuelve por procedimientos numéricos con las siguientes condiciones iniciales t=0, θ=0, ${\left(\frac{d\theta }{dt}\right)}_0=\frac{v_0}{R}$ . Donde v₀ es la velocidad inicial. En un apartado más abajo, resolveremos utilizando MATLAB la ecuación del movimiento. En la simulación se utiliza el procedimiento de Runge-Kutta

La partícula se detiene o deja de tener contacto con la cúpula

La ecuación del movimiento se puede integrar para obtener una expresión de la velocidad v en función del parámetro θ.

${\displaystyle \begin{array}{l}\frac{dv}{dt}=g\sin \theta -\mu g\cos \theta +\mu \frac{v^2}{\rho }\\ v\frac{dv}{ds}=g\sin \theta -\mu g\cos \theta +\mu \frac{v^2{\cos }^2\theta }{R}\\ \frac{1}{2}\frac{d{v}^2}{Rd\theta }{\cos }^2\theta =g\sin \theta -\mu g\cos \theta +\mu \frac{v^2{\cos }^2\theta }{R}\end{array}}$

Llamando x=v²/(Rg), nos queda la ecuación diferencial

${\displaystyle \frac{dx}{d\theta }-2\mu x=\frac{2}{\cos \theta }\left(\tan \theta -\mu \right)}$

La solución de la ecuación diferencial se compone de dos términos: la solución de la ecuación diferencial homogénea y la particular

La solución de la ecuación diferencial homogénea es

${\displaystyle \frac{dx}{d\theta }-2\mu x=0\frac{dx}{x}=2\mu ·d\theta {\displaystyle \int \frac{dx}{x}={\displaystyle \int 2\mu ·d\theta }}}$

Integrando ambos miembros obtenemos lnx=2μθ+cte, o bien,x₁=D·exp(2μθ)

Buscamos una solución particular de la forma, donde u(θ) es deconocida

${\displaystyle x_2=D{e}^{2\mu \theta }u(\theta )}$

Introducimos x₂ en la ecuación diferencial

${\displaystyle \begin{array}{l}2\mu D{e}^{2\mu \theta }u(\theta )+D{e}^{2\mu \theta }\frac{du}{d\theta }-2\mu D{e}^{2\mu \theta }u(\theta )=\frac{2}{\cos \theta }\left(\tan \theta -\mu \right)\\ D{e}^{2\mu \theta }\frac{du}{d\theta }=\frac{2}{\cos \theta }\left(\tan \theta -\mu \right)\\ u(\theta )=\frac{2}{D}{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta \\ x_2=2e^{2\mu \theta }{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta \end{array}}$

La solución de la ecuación diferencial, es la suma de la solución de la homogénea y de la particular x=x₁+x₂

${\displaystyle \frac{v^2}{Rg}=D{e}^{2\mu \theta }+2e^{2\mu \theta }{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta }$

La constante D se determina a partir de las condiciones iniciales, para θ=0, v=v₀

Finalmente, la ecuación que nos proporciona la velocidad v en función del parámetro θ, es

${\displaystyle \frac{v^2}{Rg}=\frac{v_0^2}{Rg}{e}^{2\mu \theta }+2e^{2\mu \theta }{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta }$

La reacción N de la cúpula se calcula conociendo v² en la posición dada por el parámetro θ

${\displaystyle \begin{array}{l}mg\cos \theta -N=m\frac{v^2}{\rho }\\ \frac{N}{mg}=\cos \theta \left(1-\left(\frac{v^2}{Rg}\right)\cos \theta \right)\end{array}}$

Si no hay rozamiento, μ=0

${\displaystyle \begin{array}{l}\frac{v^2}{Rg}=\frac{v_0^2}{Rg}+2{\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{\sin \theta }{{\cos }^2\theta }}d\theta \\ \frac{v^2}{Rg}=\frac{v_0^2}{Rg}+2\left(\frac{1}{\cos \theta }-1\right)\end{array}}$

La misma expresión se obtiene aplicando el principio de conservación de la energía.

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_0^2+mgR=\frac{1}{2}m{v}^2+mgy\\ v^2=v_0^2+2g\left(R-R(2-\cosh \phi )\right)\\ \frac{v^2}{Rg}=\frac{v_0^2}{Rg}+2\left(\sqrt{1+{\sinh }^2\phi }-1\right)\\ \frac{v^2}{Rg}=\frac{v_0^2}{Rg}+2\left(\sqrt{1+{\tan }^2\theta }-1\right)\\ \frac{v^2}{Rg}=\frac{v_0^2}{Rg}+2\left(\frac{1}{\cos \theta }-1\right)\end{array}}$

La partícula, deja de tener contacto con la cúpula para el valor del parámetro θ_s tal que N=0.

${\displaystyle \begin{array}{l}mg\cos \theta -N=m\frac{v^2}{\rho }\\ mg\cos \theta =m\frac{v^2{\cos }^2\theta }{R}\\ \frac{1}{\cos {\theta }_s}=2-\frac{v_0^2}{Rg}\end{array}}$

Si la velocidad inicial v₀=0, θ_s=π/3 (60°). En el caso de una cúpula semiesférica θ_s=arccos(2/3) (48°), en el caso de una cúpula en forma de cicloide, θ_s=π/4 (45°). La partícula permanece en el vértice θ=0, que es una posición de equilibrio inestable, hasta que una pequeña perturbación la lleva a deslizar a lo largo de la cúpula, tal como se ha descrito en la página Movimiento sobre una cúpula semiesférica, sin rozamiento

Una vez alcanzada la posición θ_s, la partícula describe un movimiento parabólico. Dicha posición (x,y) se calcula mediante la relación entre la pendiente θ y el parámetro φ y ecuaciones paramétricas de la catenaria

sinhφ=tanθ
x=Rφ
y=R(2-cosh(φ))=R(2-1/cosθ)

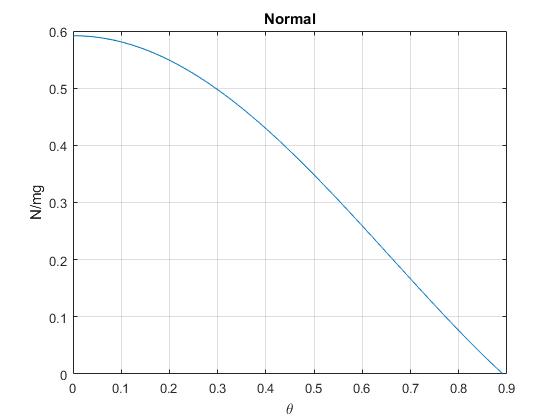
Representamos la reacción N/mg en función del parámetro θ hasta el ángulo crítico θ_s, posición en la que se anula N=0

R=1;
v0=2; %velocidad inicial
v2=@(x) v0^2+2*R*9.8*(1./cos(x)-1); %cuadrado velocidad
N=@(x) cos(x).*(1-v2(x).*cos(x)/(9.8*R)); %normal

th_c=acos(1/(2-v0^2/(R*9.8))); %ángulo crítico N=0
fplot(N,[0,th_c])
grid on
xlabel('\theta')
ylabel('N/mg')
title('Normal')

Si hay rozamiento μ≠0, pueden ocurrir dos casos:

• Que la partícula deje de estar en contacto con la cúpula, es decir, la reacción N se haga cero, con v>0
• Que la partícula se detenga v=0, con N>0

Sea una cúpula en forma de catenaria de R=1, la velocidad inicial en el vértice, θ=0, es v₀=2 m/s, el coeficiente de rozamiento es μ=0.2. Representamos v²/(Rg) y N en función del parámetro θ

R=1;
mu=0.2; %coeficiente de rozamiento
v0=2; %velocidad inicial
f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);
v2=@(x) exp(2*mu*x).*(v0^2/(R*9.8)+2*integral(f,0,x)); %cuadrado velocidad
N=@(x) cos(x).*(1-v2(x).*cos(x)); %normal

subplot(2,1,1)
fplot(v2,[0,1])
grid on
ylim([0,1.5])
xlabel('\theta')
ylabel('v^2/Rg')
title('Velocidad')

subplot(2,1,2)
fplot(N,[0,1])
grid on
ylim([-0.5,1])
xlabel('\theta')
ylabel('N/mg')
title('Normal')

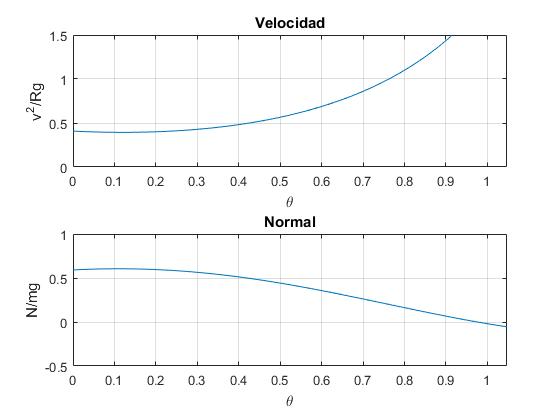
La velocidad disminuye y luego aumenta. La reacción N se hace cero para un valor crítico del parámetro θ_c, que calculamos mediante la función fzero de MATLAB. Recuérdese que la valor mayor de θ es tanθ₀=$\sqrt{3}$, θ₀=1.0472

>> fzero(N,[0,atan(sqrt(3))])
ans =    0.9758

Cambiamos el coeficiente de rozamiento a μ=0.4 y la velocidad inicial v₀=1. Representamos v²/(Rg) en función del parámetro θ

R=1;
mu=0.4; %coeficiente de rozamiento
v0=1; %velocidad inicial
f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);
v2=@(x) exp(2*mu*x).*(v0^2/(R*9.8)+2*integral(f,0,x)); %cuadrado velocidad

fplot(v2,[0,1.0472])
ylim([-0.5,1])
grid on
xlabel('\theta')
ylabel('v^2/Rg')
title('Velocidad')

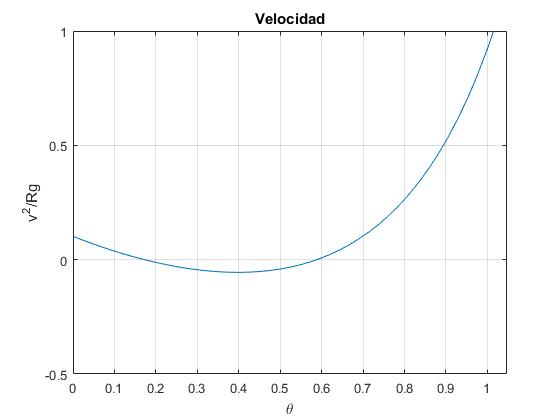
La partícula se detiene v=0, en la posición dada por el parámetro θ_c que calculamos utilizando la función fzero de MATLAB.

>> fzero(v2,[0,0.2])
ans =    0.1725

La velocidad inicial en el vértice, θ=0, es v₀=2 m/s, el coeficiente de rozamiento es μ=0.5. Representamos v²/(Rg) y N en función del parámetro θ

R=1;
mu=0.5; %coeficiente de rozamiento
v0=2; %velocidad inicial
f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);
v2=@(x) exp(2*mu*x).*(v0^2/(R*9.8)+2*integral(f,0,x)); %cuadrado velocidad
N=@(x) cos(x).*(1-v2(x).*cos(x)); %normal

subplot(2,1,1)
fplot(v2,[0,atan(sqrt(3))])
grid on
ylim([0,1.5])
xlabel('\theta')
ylabel('v^2/Rg')
title('Velocidad')

subplot(2,1,2)
fplot(N,[0,atan(sqrt(3))])
grid on
ylim([0,1.5])
xlabel('\theta')
ylabel('N/mg')
title('Normal')

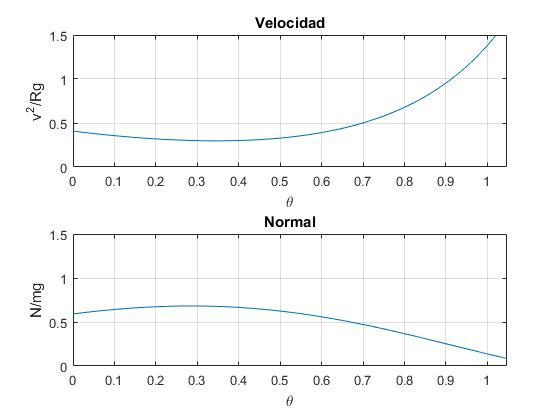
Ni la velocidad v ni la normal N se hacen cero para 0≤θ≤θ₀

Velocidad inicial crítica y ángulo crítico

Fijamos el coeficiente de rozamiento, por ejemplo, μ=0.4, y vamos cambiando la velocidad inicial v₀ con el que lanzamos la partícula en la posición θ=0.

mu=0.4; %coeficiente de rozamiento
R=1;
hold on
for v0=[1.1,1.3,1.5] %velocidades iniciales
    f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);
    v2=@(x) exp(2*mu*x).*(v0^2/(R*9.8)+2*integral(f,0,x)); %cuadrado velocidad
    fplot(v2,[0,1.0472],'displayName',num2str(v0))
end
hold off
legend('-DynamicLegend','location','northeast')
line([atan(mu),atan(mu)],[-0.05,0.2],'linestyle','--');
ylim([-0.05,0.6])
grid on
xlabel('\theta')
ylabel('v^2/Rg')
title('Velocidades')

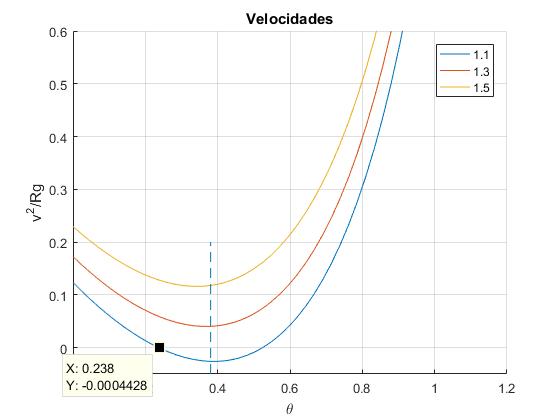
En la figura, se representa el cuadrado de la velocidad de la partícula v²/(Rg) en función del parámetro θ, para varias velocidades iniciales v₀=1.1, 1.3, 1.5 m/s. Se ha fijado el parámetro R=1.0 m

• La partícula se detiene como ocurre para la velocidad v₀=1.1, que corta el eje X, en la posición θ=0.238
• La partícula disminuye su velocidad y luego, la incrementa, como ocurre para v₀=1.3, 1.5.
• En la gráfica, se señala por una raya vertical a trazos la posición tanθ=μ,

Existe una velocidad inicial crítica v_0,c para el cual la velocidad v de la partícula presenta un mínimo v=0 en el ángulo θ_c denominado ángulo crítico.

${\displaystyle v^2({\theta }_c)=0{\left(\frac{d{v}^2}{d\theta }\right)}_{{\theta }_c}=0}$

Tenemos un sistema de dos ecuaciones, haciendo operaciones y simplificando

${\displaystyle \{\begin{array}{l}\frac{v_0^2}{Rg}+2{\displaystyle \underset{0}{\overset{{\theta }_c}{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta =0\\ 2\mu \frac{v_0^2}{Rg}{e}^{2\mu {\theta }_c}+4\mu e^{2\mu {\theta }_c}{\displaystyle \underset{0}{\overset{{\theta }_c}{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta +2\frac{\tan {\theta }_c-\mu }{\cos {\theta }_c}=0\end{array}}$

llegamos a la siguiente relación

tanθ_c=μ

Calculamos la velocidad inicial crítica v_0,c en θ=0 para la cual la partícula se detiene en θ_c.

${\displaystyle \frac{v_{0c}^2}{Rg}=-2{\displaystyle \underset{0}{\overset{\arctan \mu }{\int }}\frac{e^{-2\mu \theta }}{\cos \theta }\left(\tan \theta -\mu \right)}d\theta }$

Representamos el cuadrado de la velocidad inicial crítica, en función del coeficiente de rozamiento μ

R=1;
roza=linspace(0,4,100);
Vc=zeros(0,length(roza));
i=1;
for mu=roza
    f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);  
    Vc(i)=-2*integral(f,0,atan(mu)); %cuadrado velocidad
    i=i+1;
end
plot(roza,Vc)
grid on
xlabel('\mu')
ylabel('v^2/Rg')
title('Velocidad crítica')

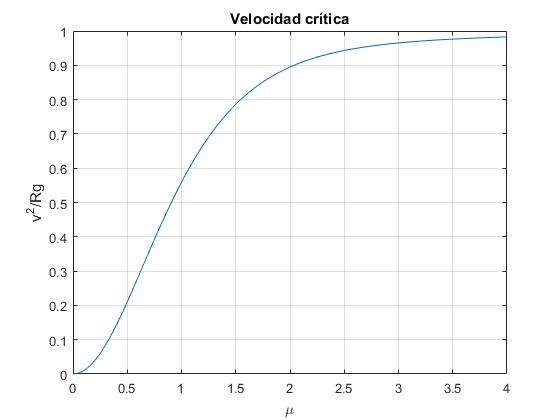
La curva divide el plano (μ, v₀) en dos regiones. Fijado el valor de μ

• Para velocidades iniciales v₀>v_0,c la partícula no se detiene, deja la cúpula
• Para velocidades iniciales v₀<v_0,c la partícula se detiene.

Balance energético

La energía de la partícula en la posición inicial es

• La energía cinética  E_k=mv₀²/2

• La energía potencial E_p=mgR

Cuando la partícula se encuentra en la posición definida por el parámetro es θ.

• La energía cinética E_k=mv²/2

• La energía potencial E_p=mgy

${\displaystyle \begin{array}{l}{E}_p=mg\left(R-R(2-\cosh \phi )\right)\\ E_p=mgR\left(\sqrt{1+{\sinh }^2\phi }-1\right)\\ E_p=mgR\left(\sqrt{1+{\tan }^2\theta }-1\right)\\ E_p=mgR\left(\frac{1}{\cos \theta }-1\right)\end{array}}$

La fuerza de rozamiento F_r=μN, tiene la misma dirección (tangencial) que el desplazamiento, el arco ds, pero de sentido contrario. El trabajo realizado por la fuerza de rozamiento es.

${\displaystyle \begin{array}{l}{W}_{nc}=-\underset{0}{\overset{\theta }{{\displaystyle \int }}}\mu N·ds=-\mu m\underset{0}{\overset{\theta }{{\displaystyle \int }}}\left(g\cos \theta -\frac{v^2}{\rho }\right)ds=\\ -\mu m\underset{0}{\overset{\theta }{{\displaystyle \int }}}\left(g\cos \theta -\frac{v^2{\cos }^2\theta }{R}\right)\frac{R}{{\cos }^2\theta }·d\theta =-\mu mgR\underset{0}{\overset{\theta }{{\displaystyle \int }}}\left(\frac{1}{\cos \theta }-\frac{v^2}{Rg}\right)d\theta \end{array}}$

El trabajo realizado por la fuerza de rozamiento W_nc<0 es igual a la diferencia entre la energía final menos la energía inicial.

${\displaystyle W_{nc}=\left(\frac{1}{2}m{v}^2+mgR\left(\frac{1}{\cos \theta }-1\right)\right)-\left(\frac{1}{2}m{v}_0^2+mgR\right)}$

Resulta

${\displaystyle \begin{array}{l}\frac{v^2}{Rg}-\frac{v_0^2}{Rg}=4-\frac{2}{\cos \theta }-2\mu \underset{0}{\overset{\theta }{{\displaystyle \int }}}\left(\frac{1}{\cos \theta }-\frac{v^2}{Rg}\right)d\theta \hfill \\ x-x_0=4-\frac{2}{\cos \theta }-2\mu \underset{0}{\overset{\theta }{{\displaystyle \int }}}\left(\frac{1}{\cos \theta }-x\right)d\theta \hfill \end{array}}$

Derivando con respecto a θ

${\displaystyle \begin{array}{l}\frac{dx}{d\theta }=\frac{2\sin \theta }{{\cos }^2\theta }-2\mu \left(\frac{1}{\cos \theta }-x\right)\\ \frac{dx}{d\theta }-2\mu x=\frac{2}{\cos \theta }\left(\tan \theta -\mu \right)\end{array}}$

La misma ecuación diferencial que obtuvimos por dinámica

Solución numérica de la ecuación del movimiento

Primero, calculamos el ángulo límite para el cual la partícula se detiene v=0, o bien, la reacción de la cúpula N=0. Después, resolvemos la ecuación diferencial del movimiento que se ha deducido al principio de esta página.

mu=0.4; %coeficiente de rozamiento
v0=2; %velocidad inicial para theta=0,
R=1;

f=@(x) (exp(-2*mu*x).*(tan(x)-mu))./cos(x);
Vc=sqrt(-2*R*9.8*integral(f,0,atan(mu))); % velocidad crítica
v2=@(x) exp(2*mu*x).*(v0^2/(R*9.8)+2*integral(f,0,x)); %cuadrado velocidad
N=@(x) cos(x).*(1-v2(x).*cos(x)); %normal/mg

if v0<Vc
    aLimite=fzero(v2,atan(mu));
    opts=odeset('events',@(t,x) stop_cupula_1(t,x));
    disp('velocidad nula')
else
    th_c=acos(1/(2-v0^2/(R*9.8)));
    aLimite=fzero(N,th_c);
    opts=odeset('events',@(t,x) stop_cupula(t,x,aLimite));
    disp('normal nula')
end

x0=[0, v0/R];
f=@(t,x) [x(2);-(2*tan(x(1))-mu)*x(2)^2+9.8*(sin(x(1))-
mu*cos(x(1)))*cos(x(1))^2/R];
tspan=[0,20]; 
[t,x]=ode45(f,tspan,x0,opts);

plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta')
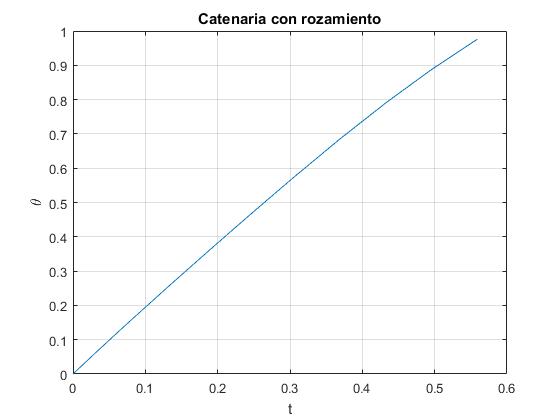
title('Catenaria con rozamiento')

Definimos dos funciones para que el proceso de integración se detenga cuando N sea cero o cuando la derivada dθ/dt sea cero.

function [value,isterminal,direction]=stop_cupula(~,x,xFin)
    value=xFin-x(1); 
    isterminal=1;
    direction=0; 
end
function [value,isterminal,direction]=stop_cupula_1(~,x)
    value=x(2); 
    isterminal=1;
    direction=0; 
end

Cuando μ=0.2 y v₀=2. La partícula deja de tener contacto con la cúpula, N=0 cuando θ=0.9758, tal como vemos en la gráfica (ordenda Y).

normal nula
>> aLimite
aLimite =    0.9758

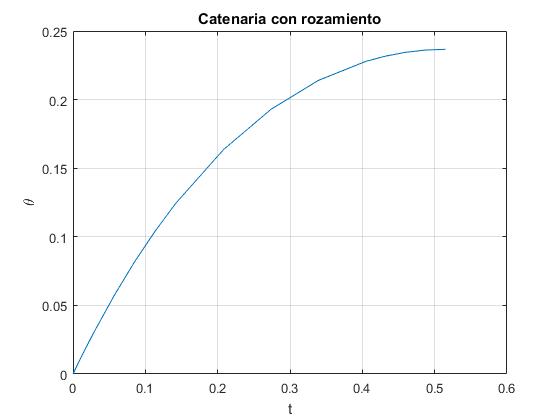
Cambiamos la velocidad inicial v₀=1.1, la partícula se detiene dθ/dt=0, para θ=0.2366.

velocidad nula
>> aLimite
aLimite =    0.2366

Actividades

Se introduce

• El coeficiente de rozamiento μ, en el control de edición titulado Rozamiento

• La velocidad inicial v₀ en la posición inicial θ=0, en el control de edición titulado V. inicial.

• La masa de la partícula se ha fijado en m=1 kg

• El parámetro R=1 m (vértice de la catenaria).

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la partícula deslizando sobre la cúpula. Sobre la partícula se dibujan las fuerzas: peso mg, reacción N, y fuerza de rozamiento F_r.

En la parte superior derecha, se proporcionan los datos de

• el tiempo t en segundos

• El valor del parámetro θ que determina la posición d ela partícula en la cúpula

• la velocidad v de la partícula en m/s.

Cuando la reacción N se hace cero, se muestran los datos de la a velocidad v en la posición θ_c en la que la partícula deja de tener contacto con la cúpula.

El círculo situado en la parte superior izquierda representa la energía total de la partícula, la porción de color rojo representa la energía cinética, y la porción azul, la energía potencial. Observamos que la energía potencial se va transformando en energía cinética, pero la suma de los valores de ambas clases de energía no se mantiene constante a lo largo de la trayectoria de la partícula si hay rozamiento. El trabajo de la fuerza de rozamiento viene indicado por la porción negra del círculo de mayor radio.

Mediante una línea roja a trazos se señala el valor límite del parámetro θ, para el cual la reacción N=0 o la partícula se detiene, su velocidad v=0

Referencias

Felipe González-Cataldo, Gonzalo Gutiérrez. Julio M. Yáñez. Sliding down an arbitrary curve in the presence of friction. Am. J. Phys. 85 (2) February 2017, 108-114