Dinámica de una partícula unida a dos cuerdas elásticas

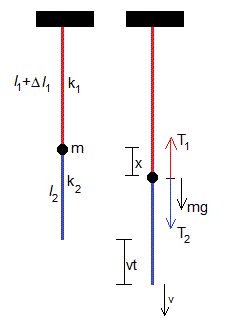
Supongamos un cuerpo de masa m que cuelga de una cuerda de constante k₁, otra cuerda de constante k₂ cuelga del cuerpo. Se tira de la cuerda inferior de modo que su extremo libre se mueve con velocidad constante v. Suponiendo que las cuerdas no tienen masa y se comportan de acuerdo a la ley de Hooke (fuerza proporcional a la deformación). Vamos a calcular la altura x del peso en función del tiempo t y las tensiones T₁ y T₂ de las dos cuerdas.

En el instante t=0, la tensión de la cuerda roja es T₁=mg y su deformación es Δl₁=mg/k₁. La tensión de la cuerda azul es,T₂=0.

Situamos el origen en esta posición del cuerpo (figura izquierda) con el eje X apuntando hacia abajo

En el instante t, la longitud de la cuerda azul es l₂+vt-x, tal como vemos en la figura. De modo que la tensión T₂ de esta cuerda es

T₂=k₂(l₂+vt-x-l₂)=k₂(vt-x)

La tensión de la cuerda roja es

T₁=k₁x+mg

Ecuación del movimiento

El cuerpo de masa m, se mueve bajo la acción de las fuerzas T₂, T₁ (las tensiones de las cuerdas) y su peso mg, en los sentidos señalados en la figura de la derecha. La ecuación del movimiento es

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = k_{2} (v t - x) + m g - (k_{1} x + m g) \\ \frac{d^{2} x}{d t^{2}} + \frac{k_{1} + k_{2}}{m} x = \frac{k_{2} v}{m} t \end{array}$

La solución particular de esta ecuación diferencial es x₁=Ct, introduciendo x₁ en la ecuación diferencial obtenemos el valor de C

$C = \frac{k_{2} v}{k_{1} + k_{2}}$

La solución de la homogénea es Asin(ωt)+Bcos(ωt). La solución completa es

$\begin{array}{l} x = A \sin (ω t) + B \cos (ω t) + \frac{k_{2} v}{m ω^{2}} t ω^{2} = \frac{k_{1} + k_{2}}{m} \\ \frac{d x}{d t} = A ω \cos (ω t) - B ω \sin (ω t) + \frac{k_{2} v}{m ω^{2}} \end{array}$

A y B vienen determinados por las condiciones iniciales, en el instante t=0, x=0, dx/dt=0.

$\begin{array}{l} x = \frac{k_{2} v}{m ω^{3}} (ω t - \sin (ω t)) \\ \frac{d x}{d t} = \frac{k_{2} v}{m ω^{2}} (1 - \cos (ω t)) \end{array}$

Las tensiones de las cuerdas son

$\begin{array}{l} T_{1} = k_{1} x + m g = \frac{k_{2} v}{m ω^{3}} (k_{1} ω t - k_{1} \sin (ω t)) + m g \\ T_{2} = k_{2} (v t - x) = \frac{k_{2} v}{m ω^{3}} (k_{1} ω t + k_{2} \sin (ω t)) \end{array}$

Ambas tensiones se hacen iguales T₂=T₂, en el instante t_c

$\sin (ω t_{c}) = \frac{m ω g}{k_{2} v}$

y esto ocurre siempre que

$v \geq \frac{m g ω}{k_{2}}$

La expresión a la derecha del símbolo ≥ se denomina velocidad crítica v_c

Dos trozos de la misma cuerda

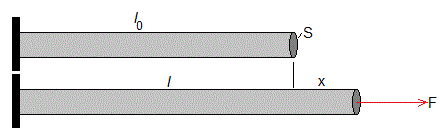
Una cuerda sometida a un esfuerzo de tracción experimenta una deformación que consiste en el aumento de longitud y en una contracción de su sección. Supondremos que el aumento de longitud es el efecto dominante, sobre todo en cuerdas largas y de pequeña sección.

$\frac{F}{S} = Y \frac{l - l_{0}}{l_{0}}$

Donde S es la sección de la cuerda y Y es una constante de proporcionalidad característica de cada material que se denomina módulo de elasticidad o módulo de Young.

$F = k x, k = \frac{S Y}{l_{0}}, x = l - l_{0}$

Dividimos la cuerda en dos trozos de longitudes l₁ y l₂. Se cumple que

$k_{1} l_{1} = k_{2} l_{2}$

La frecuencia angular ω vale

$ω^{2} = \frac{k_{1}}{m} (1 + \frac{l_{1}}{l_{2}})$

Las tensiones de la cuerdas superior e inferior valen, respectivamente

$\begin{array}{l} T_{1} = \frac{k_{1} l_{1}}{l_{1} + l_{2}} \frac{v}{ω} (ω t - \sin (ω t)) + m g \\ T_{2} = \frac{k_{1} l_{1}}{l_{1} + l_{2}} \frac{v}{ω} (ω t + \frac{l_{1}}{l_{2}} \sin (ω t)) \end{array}$

La velocidad crítica v_c

$v_{c} = \frac{g}{l_{1}} \sqrt{\frac{m}{k_{1}} (l_{1} + l_{2}) \frac{l_{2}}{l_{1}}}$

Ejemplo

Masa de la partícula, m=1 kg
Constante elástica de la cuerda superior, k₁=10 N/m
Longitud de la cuerda superior, l₁=1.0 m
Longitud de la cuerda inferior, l₂=0.2 m
Aceleración de la gravedad, g=10 m/s²
Tensión máxima que pueden soportar las cuerdas, T_m=20 N

Con estos datos, tenemos que la velocidad crítica v_c=1.55 m/s y la frecuencia angular ω=7.75 rad/s.

Representamos las tensiones T₁ y T₂ en función del tiempo t, en los casos siguientes

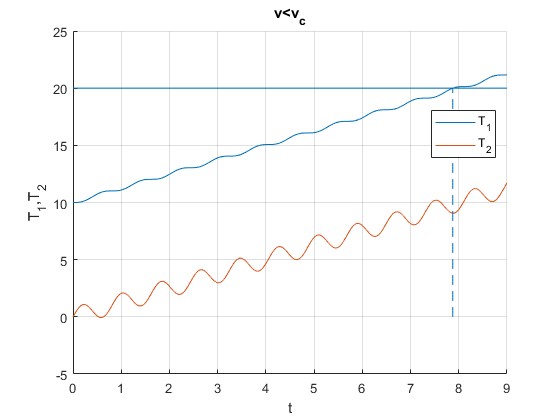
v<v_c. Por ejemplo, v=0.15 m/s

La cuerda superior alcanza la máxima tensión que soporta en el instante t=7.87 s, que es la raíz de la ecuación transcendente f(t)=T₁(t)-T_m

m=1; % masa
k1=10; % constante elástica
l2=0.2; %segundo trozo
l1=1.0; %primer trozo
g=10; %aceleración de la gravedad
Tm=20; %fuerza máxima
vc=g*sqrt(m*(l1+l2)*l2/(k1*l1))/l1; %velocidad crítica
w=sqrt(k1*(l1+l2)/(m*l2)); %frecuencia angular

v=0.15; %velocidad del extremo de la cuerda v<vc
hold on
T1=@(t) k1*l1*v*(w*t-sin(w*t))/((l1+l2)*w)+m*g;
fplot(T1,[0,9])
T2=@(t) k1*l1*v*(w*t+l1*sin(w*t)/l2)/((l1+l2)*w);
fplot(T2,[0,9])
line([0,9],[Tm,Tm])
f=@(t) T1(t)-Tm;
tf=fzero(f,[0,9]);
line([tf,tf],[0,T1(tf)],'lineStyle','--')
disp(tf)
hold off
grid on
xlabel('t')
ylabel('T_1,T_2')
legend('T_1','T_2','Location', 'best')
title('v<v_c')

7.8752

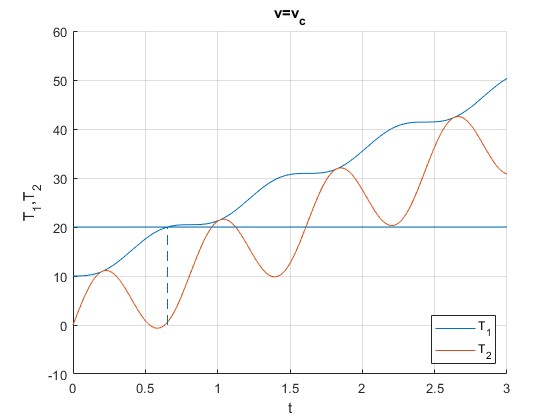
v=v_c. v=1.55 m/s

La cuerda superior alcanza la máxima tensión que soporta en el instante t=0.65 s, que es la raíz de la ecuación transcendente f(t)=T₁(t)-T_m

m=1; % masa
k1=10; % constante elástica
l2=0.2; %segundo trozo
l1=1.0; %primer trozo
g=10; %aceleración de la gravedad
Tm=20; %fuerza máxima
vc=g*sqrt(m*(l1+l2)*l2/(k1*l1))/l1; %velocidad crítica
w=sqrt(k1*(l1+l2)/(m*l2)); %frecuencia angular

v=vc; %velocidad del extremo de la cuerda v<vc
hold on
T1=@(t) k1*l1*v*(w*t-sin(w*t))/((l1+l2)*w)+m*g;
fplot(T1,[0,3])
T2=@(t) k1*l1*v*(w*t+l1*sin(w*t)/l2)/((l1+l2)*w);
fplot(T2,[0,3])
line([0,3],[Tm,Tm])
f=@(t) T1(t)-Tm;%w*t-sin(w*t)-(Tm-m*g)*(l1+l2)*w/(k1*l1*v);
tf=fzero(f,[0,3]);
line([tf,tf],[0,T1(tf)],'lineStyle','--')
disp(tf)
hold off
grid on
xlabel('t')
ylabel('T_1,T_2')
legend('T_1','T_2','Location', 'best')
title('v=v_c')

  0.6532

v>v_c. Por ejemplo, v=3.10 m/s

La cuerda inferior alcanza la máxima tensión que soporta en el instante t=0.16 s, que es la raíz de la ecuación transcendente f(t)=T₂(t)-T_m

m=1; % masa
k1=10; % constante elástica
l2=0.2; %segundo trozo
l1=1.0; %primer trozo
g=10; %aceleración de la gravedad
Tm=20; %fuerza máxima
vc=g*sqrt(m*(l1+l2)*l2/(k1*l1))/l1; %velocidad crítica
w=sqrt(k1*(l1+l2)/(m*l2)); %frecuencia angular

v=3.1; %velocidad del extremo de la cuerda v<vc
hold on
T1=@(t) k1*l1*v*(w*t-sin(w*t))/((l1+l2)*w)+m*g;
fplot(T1,[0,3])
T2=@(t) k1*l1*v*(w*t+l1*sin(w*t)/l2)/((l1+l2)*w);
fplot(T2,[0,3])
line([0,3],[Tm,Tm])
f=@(t) T2(t)-Tm;
tf=fzero(f,[0,0.2]);
line([tf,tf],[0,T1(tf)],'lineStyle','--')
disp(tf)
hold off
grid on
xlabel('t')
ylabel('T_1,T_2')
legend('T_1','T_2','Location', 'best')
title('v>v_c')

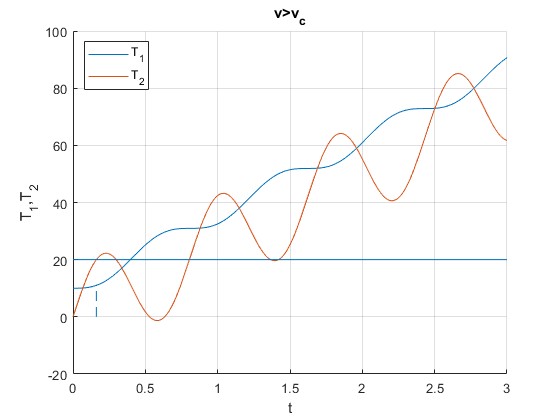
0.1615

Si cambiamos la tensión máxima a T_m=25 N, la cuerda superior alcanza la tensión máxima en el instante t=0.50 s

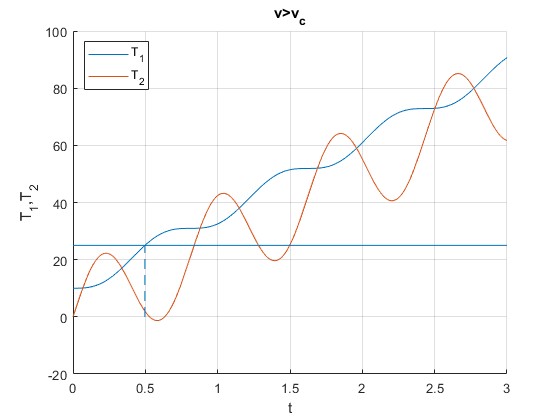
0.4968

Energías

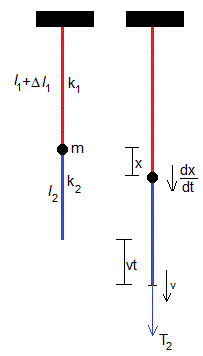
En la figura de la izquierda, tenemos la situación inicial, la cuerda roja está deformada mg/k₁. La energía inicial es

$E_{0} = \frac{1}{2} k_{1} {(\frac{m g}{k_{1}})}^{2}$

Al cabo de un tiempo t, el trabajo W de la fuerza que aplicamos en el extremo libre T₂ para que se mueva con velocidad v constante es

$\begin{array}{l} W = \int_{0}^{t} T_{2} v \cdot d t = \int_{0}^{t} \frac{k_{2} v}{m ω^{3}} (k_{1} ω t + k_{2} \sin (ω t)) v d t = \\ \frac{1}{2} \frac{k_{1} k_{2} v^{2}}{m ω^{2}} t^{2} + \frac{k_{2}^{2} v^{2}}{m ω^{4}} - \frac{k_{2}^{2} v^{2}}{m ω^{4}} \cos (ω t) \end{array}$

Este trabajo se convierte en energía elástica de las cuerdas deformadas, energía potencial y cinética del cuerpo de masa m

$E = \frac{1}{2} k_{1} {(\frac{m g}{k_{1}} + x)}^{2} + \frac{1}{2} k_{2} {(v t - x)}^{2} - m g x + \frac{1}{2} m {(\frac{d x}{d t})}^{2}$

Comprobamos después de una larga simplificación que W=E-E₀

Actividades

Se introduce

La constante elástica k₁ de la cuerda roja en el control titulado Constante k₁
La velocidad constante del extremo de la cuerda azul en el control titulado Velocidad

Se ha fijado

La longitud de la cuerda roja L₁=0.5 y la longitud de la cuerda azul L₂=1.0
La masa del cuerpo m=1
La constante elástica de la cuerda azul k₂=100

Se pulsa el botón titulado Nuevo

Observamos el movimiento del sistema y a la derecha, la representación gráfica de las tensiones T₁/mg y de T₂/mg en función de ωt

En la parte inferior izquierda, se proporciona el valor del parámetro p

$\frac{k_{2} v}{m ω g}$

Constante k₁:
Velocidad:

Se aplica una fuerza al extremo del muelle inferior

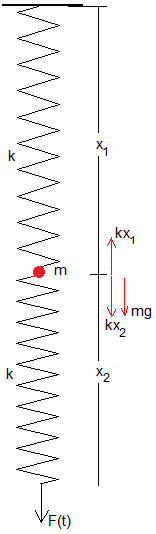
Consideremos una variante de este problema. El cuerpo de masa m cuelga de un muelle elástico de constante k y de longitud cero sin deformar. El muelle se rompe si se deforma más allá de cierto límite l_c>mg/k. Otro muelle de las mismas características cuelga del cuerpo

Se aplica una fuerza F(t) al extremo libre de este muelle. Veremos que

si tiramos rápidamente, el muelle inferior se rompe
si tiramos poco a poco, el muelle superior se rompe

Determinaremos que fuerza hay que aplicar para que ambos muelles se rompan simultáneamente.

Como vemos en el dibujo, la ecuación del movimiento de la partícula de masa m

$m \frac{d^{2} x_{1}}{d t^{2}} = m g - k x_{1} + k x_{2}$

La fuerza aplicada F(t) origina la deformación del muelle inferior.

$k x_{2} = F (t)$

Eliminando x₂, obtenemos una ecuación diferencial en x₁

$m \frac{d^{2} x_{1}}{d t^{2}} + k x_{1} = m g + F (t)$

La solución de la homogénea es conocida x=Asin(ωt)+Bcos(ωt), con ω²=k/m

La expresión de la fuerza F(t) determina la solución particular de la ecuación diferencial. Consideremos un caso sencillo: la fuerza se incrememta linealmente con el tiempo, F(t)=αt.

La solución particular tiene la forma y=Ct+D. Introduciéndola en la ecuación diferencial se obtiene C=α/k y D=mg/k

La solución completa es

$\begin{array}{l} x_{1} = A \sin (ω t) + B \cos (ω t) + \frac{α}{k} t + \frac{m g}{k} \\ \frac{d x_{1}}{d t} = ω A \cos (ω t) - ω B \sin (ω t) + \frac{α}{k} \end{array}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, x₁=mg/k, dx₁/dt=0

$\begin{array}{l} x_{1} = \frac{α}{k} t + \frac{m g}{k} - \frac{α}{k ω} \sin (ω t) \\ x_{2} = \frac{α}{k} t \end{array}$

Para que los dos muelles se rompan simultáneamente, x₂=l_c, en el instante t₀=kl_c/α. Poniendo x₁=l_c, obtenemos una ecuación transcendente de la que despejamos el parámetro α

$\begin{array}{l} l_{c} = \frac{α}{k} t_{0} + \frac{m g}{k} - \frac{α}{k ω} \sin (ω t_{0}) \\ \frac{m g ω}{α} = \sin (ω \frac{k l_{c}}{α}) \end{array}$

Para que exista solución, mgω/α≤1

k=10; %constante de los muelles
m=1; %masa de la partícula
lc=1.5; %se rompe 
w=sqrt(k/m); %frecuencia angular

>> f=@(x) sin(w*k*lc/x)-m*9.8*w/x;
>> fzero(f,20)
ans =   31.0170

Trabajo y energía

La energía inicial en el instante t=0 es la suma de la energía potencial del muelle superior deformado x₁=mg/k y la energía potencial de la partícula de masa m

$E_{0} = \frac{1}{2} k {(\frac{m g}{k})}^{2} - m g \frac{m g}{k} = - \frac{1}{2} \frac{m^{2} g^{2}}{k}$

La energía potencial elástica de los muelles deformados es

$\begin{array}{l} E_{p} = \frac{1}{2} k x_{1}^{2} + \frac{1}{2} k x_{2}^{2} = \frac{1}{2} k {(\frac{α}{k} t + \frac{m g}{k} - \frac{α}{k ω} \sin (ω t))}^{2} + \frac{1}{2} k {(\frac{α}{k} t)}^{2} = \\ \frac{α^{2}}{k} t^{2} + \frac{1}{2} \frac{m^{2} g^{2}}{k} + \frac{1}{2} \frac{α^{2}}{k ω^{2}} \sin^{2} (ω t) + \frac{α m g}{k} t - \frac{α^{2}}{k ω} t \sin (ω t) - \frac{m g α}{k ω} \sin (ω t) \end{array}$

La energía cinética de la partícula de masa m

$E_{k} = \frac{1}{2} m {(\frac{d x_{1}}{d t})}^{2} = \frac{1}{2} m {(\frac{α}{k} - \frac{α}{k} \cos (ω t))}^{2} = \frac{1}{2} m {(\frac{α}{k})}^{2} (1 - 2 \cos (ω t) + \cos^{2} (ω t))$

La energía potencial gravitatoria de la partícula de masa m es

$E_{g} = - m g x_{1} = - m g (\frac{α}{k} t + \frac{m g}{k} - \frac{α}{k ω} \sin (ω t))$

El trabajo W es la suma de los trabajos infinitesimales F(t)·d(x₁+x₂), el segundo término es el desplazamiento del extremo del muelle inferior donde se aplica la fuerza.

$\begin{array}{l} W = \int_{0}^{t} F (t) (d x_{2} + d x_{1}) = \int_{0}^{t} α t \frac{α}{k} (2 - \cos (ω t)) d t = \\ \frac{α^{2}}{k} t^{2} - \frac{α^{2}}{k ω} \sin (ω t) - \frac{α^{2}}{k ω^{2}} \cos (ω t) + \frac{α^{2}}{k ω^{2}} = \\ \frac{α^{2}}{k} t^{2} - \frac{α^{2}}{k ω} \sin (ω t) - \frac{m α^{2}}{k^{2}} \cos (ω t) + \frac{m α^{2}}{k^{2}} \end{array}$

El trabajo W se invierte en modificar la energía cinética de la partícula de masa m, su energía potencial gravitatoria, su energía cinética y en defomar los muelles.

$W = E_{k} + E_{p} + E_{g} - E_{0}$

Después de hacer operaciones comprobamos que la suma de las energías cinética y potencial (elástica y gravitatoria) menos la energía inicial es igual al trabajo de la fuerza F(t)

Ejemplos

Definimos el sistema:

Masa de la partícula m=1 kg
Constante elástica de los dos muelles, k=10 N/m
Coeficiente de la fuerza, α=9 kgm/s³
Los muelles se rompen cuando se deforman, l_c=1.5 m

Representamos x₁ y x₂ en función del tiempo. Calculamos el instante t₁ cuando se rompe el muelle superior y el instante t₂, cuando se rompe el muelle inferior

k=10; %constante de los muelles
alfa=9; %fuerza
m=1; %masa de la partícula
lc=1.5; %se rompe 
 
w=sqrt(k/m);
x1=@(t) alfa*t/k+m*9.8/k-alfa*sin(w*t)/(k*w);
x2=@(t) alfa*t/k;
f=@(t) x1(t)-lc;
t1=fzero(f,[0,2]);
t2=k*lc/alfa;
 
hold on
fplot(x1,[0,2])
fplot(x2,[0,2])
line([0,t2],[lc,lc],'color','k','lineStyle','--')
line([t1,t1],[0,lc],'color','k','lineStyle','--')
line([t2,t2],[0,lc],'color','k','lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('x')
legend('x_1','x_2','location','northwest')
title('Muelles')

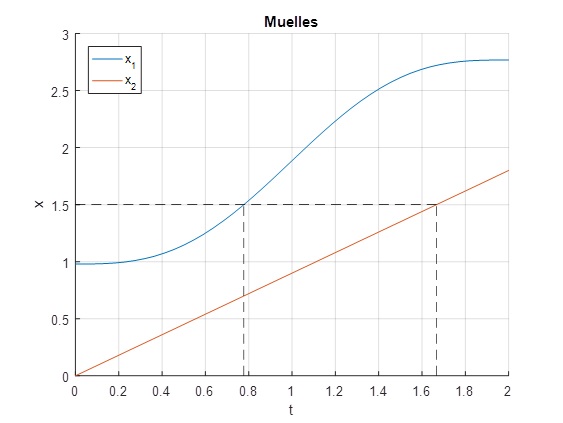
El muelle superior se rompe antes

En este ejemplo, cambiamos el parámetro α=50

k=10; %constante de los muelles
alfa=50; %fuerza
m=1; %masa de la partícula
lc=1.5; %se rompe 
 
w=sqrt(k/m);
x1=@(t) alfa*t/k+m*9.8/k-alfa*sin(w*t)/(k*w);
x2=@(t) alfa*t/k;
f=@(t) x1(t)-lc;
t1=fzero(f,[0,pi/w]);
t2=k*lc/alfa;
 
hold on
fplot(x1,[0,2])
fplot(x2,[0,2])
line([0,t1],[lc,lc],'color','k','lineStyle','--')
line([t1,t1],[0,lc],'color','k','lineStyle','--')
line([t2,t2],[0,lc],'color','k','lineStyle','--')
hold off
grid on
xlabel('t')
ylabel('x')
legend('x_1','x_2','location','northwest')
title('Muelles')

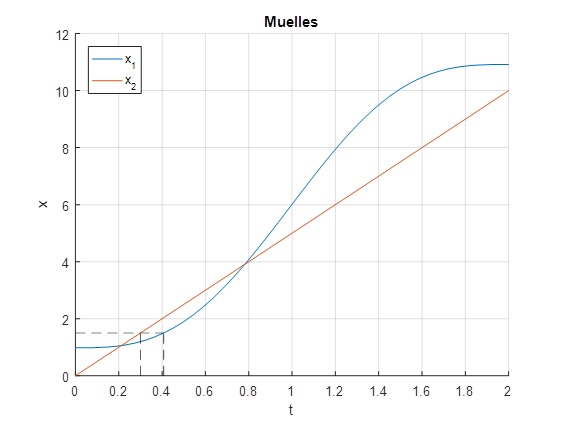
El muelle inferior se rompe antes

Para que los dos muelles se rompan al mismo tiempo, hemos calculado el valor del parámetro α=31.070

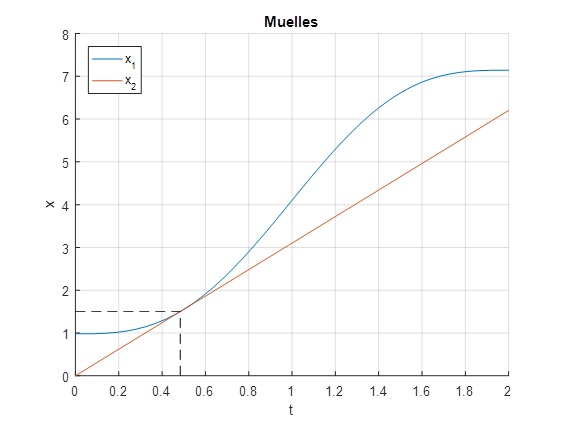
Referencias

Hiroyuki Shima. Analytic expression for the pull-or-jerk experiment. Eur. J. Phys. 35(2014) 065016

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1035, pp. 46-49

WANG Xiao-ying，WANG Ming-li，HOU Yan-xue. Thinking about a typical mechanical problem. College Physics. Vol．39 N° 1, Jan．2020