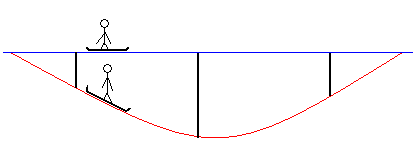
Movimiento a lo largo del puente

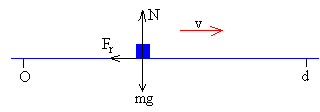
Las fuerzas sobre el esquiador son:

• El peso, mg
• La reacción de la superficie circular sobre la que desliza, N
• La fuerza de rozamiento que se opone al movimiento, F_r=μN

Hay equilibrio en el sentido vertical N=mg

Aplicamos la segunda ley de Newton al movimiento horizontal

ma=-F_r

Como la aceleración es constante a=-μg, si v₀ es la velocidad inicial del esquiador al principio del puente, al cabo de un cierto tiempo t la velocidad del esquiador ha disminuido

v=v₀-μgt

El esquiador se habrá desplazado a lo largo del puente, en el instante t su posición es

${\displaystyle x=v_{0}t-\frac{1}{2}g{t}^2}$

Si el punte tiene una longitud d, pueden ocurrir dos casos:

• Que el esquiador se pare antes de llegar al final del puente, cuando v=0,

${\displaystyle x=\frac{v_0^2}{2\mu g}}$

• Que el esquiador atraviese el puente, y llegue al final con velocidad v.

El trabajo de la fuerza de rozamiento se invierte en modificar la energía cinética de la partícula

${\displaystyle -F_{r}d=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2{v}^2=v_0^2-2\mu gd}$

Movimiento a lo largo del valle

La forma del valle puede ser descrita por una función continua que esté por debajo del segmento de la recta que conecta el punto inicial y el punto final. En este caso, el valle lo construiremos conectando cuatro arcos de circunferencia, del mismo ángulo α y radio R, tal como se muestra en la línea de color rojo, en la figura.

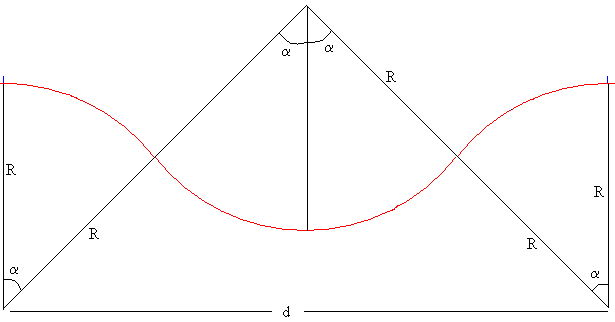
La distancia horizontal entre el punto de partida y el de llegada del esquiador es

d=4·R·senα.

Primer arco de circunferencia

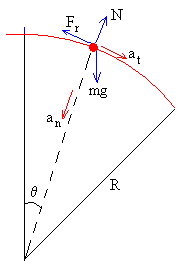
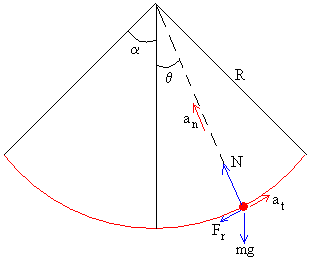
En la figura, se muestra las fuerzas sobre la partícula

• El peso, mg
• La reacción de la superficie circular sobre la que desliza, N
• La fuerza de rozamiento que se opone al movimiento, F_r=μN

La ecuación del movimiento a lo largo de la dirección radial es

${\displaystyle mg\cos \theta -N=m{a}_n{a}_n=\frac{v^2}{R}}$

La ecuación del movimiento a lo largo de la dirección tangencial es

ma_t=mg·sinθ-F_r  con F_r=μN, y a_t=dv/dt

Combinando ambas ecuaciones obtenemos

${\displaystyle \frac{dv}{dt}=g\sin \theta -\mu g\cos \theta +\mu \frac{v^2}{R}}$

Llamando x=v²/(Rg), nos queda la ecuación diferencial

${\displaystyle \frac{dx}{d\theta }-2\mu x=2(\sin \theta -\mu \cos \theta )}$

La solución de la ecuación diferencial se compone de dos términos:

La solución particular x₁=Asinθ+Bcosθ

Introduciendo la solución particular en la ecuación diferencial obtenemos los valores de los coeficientes A y B

${\displaystyle A=\frac{-6\mu }{4{\mu }^2+1}B=-\frac{2-4{\mu }^2}{4{\mu }^2+1}}$

Buscamos la solución de la ecuación diferencial homogénea

${\displaystyle \frac{dx}{d\theta }-2\mu x=0\frac{dx}{x}=2\mu ·d\theta {\displaystyle \int \frac{dx}{x}={\displaystyle \int 2\mu ·d\theta }}}$

Integrando ambos miembros obtenemos lnx=2μθ+cte, o bien,  x₂=C·exp(2μθ)

La solución completa es x=x₁+x₂

${\displaystyle \frac{v^2}{Rg}=C\exp (2\mu \theta )+\frac{-6\mu ·\sin \theta -(2-4{\mu }^2)\cos \theta }{4{\mu }^2+1}}$     (1)

La constante C se determina a partir de las condiciones iniciales, para θ=0, v=v₀

Si hay rozamiento μ≠0, pueden ocurrir tres casos:

• Que la partícula deje de estar en contacto con la pista, es decir, la reacción N se haga cero, para θ= θ_c

• Que la partícula se detenga v=0, con N>0

• Que la partícula continúe su movimiento en el segundo tramo

En el primer caso y una vez alcanzada la posición θ_c, la partícula describe un movimiento parabólico.

Ecuación diferencial del movimiento:

Poniendo v=R·dθ/dt, obtenemos la ecuación diferencial del movimiento

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{g}{R}(\sin \theta -\mu \cos \theta )+\mu {\left(\frac{d\theta }{dt}\right)}^2}$

que se resuelve por procedimientos numéricos con las condiciones iniciales t=0, θ=0, dθ/dt=v₀/R.

Cuando θ=α, el esquiador abandona el primer arco de circunferencia y entra en el segundo.

Segundo y tercer arco de circunferencia

La ecuación del movimiento a lo largo de la dirección radial es

${\displaystyle N-mg\cos \theta =m{a}_n{a}_n=\frac{v^2}{R}}$

La ecuación del movimiento a lo largo de la dirección tangencial es

ma_t=-mg·sinθ-F_r

Combinando ambas ecuaciones obtenemos

${\displaystyle \frac{dv}{dt}=-g\sin \theta -\mu g\cos \theta -\mu \frac{v^2}{R}}$

Llamando x=v²/(Rg), nos queda la ecuación diferencial

${\displaystyle \frac{dx}{d\theta }+2\mu x=-2(\sin \theta +\mu \cos \theta )}$

La solución de la ecuación diferencial se compone de dos términos:

La solución particular x₁=Asinθ+Bcosθ

Introduciendo la solución particular en la ecuación diferencial obtenemos los valores de los coeficientes A y B

${\displaystyle A=\frac{-6\mu }{4{\mu }^2+1}B=\frac{2-4{\mu }^2}{4{\mu }^2+1}}$

Buscamos la solución de la ecuación diferencial homogénea

${\displaystyle \frac{dx}{d\theta }+2\mu x=0\frac{dx}{x}=-2\mu ·d\theta {\displaystyle \int \frac{dx}{x}=-{\displaystyle \int 2\mu ·d\theta }}}$

Integrando ambos miembros obtenemos lnx=-2μθ+cte, o bien, x₂=C·exp(-2μθ)

La solución completa es x=x₁+x₂

${\displaystyle \frac{v^2}{Rg}=C\exp (-2\mu \theta )+\frac{-6\mu ·\sin \theta +(2-4{\mu }^2)\cos \theta }{4{\mu }^2+1}}$  (2)

La constante C se determina a partir de las condiciones iniciales, para θ=-α, v=v₁, donde v₁ es la velocidad del esquiador al finalizar el primer tramo.

Si hay rozamiento μ≠0, pueden ocurrir dos casos:

• Que la partícula se detenga v=0

• Que continúe su movimiento en el cuarto tramo.

Ecuación diferencial del movimiento:

Poniendo v=R·dθ/dt, obtenemos la ecuación diferencial del movimiento

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{g}{R}(\sin \theta +\mu \cos \theta )-\mu {\left(\frac{d\theta }{dt}\right)}^2}$

que se resuelve por procedimientos numéricos con las condiciones iniciales t=t₁, θ=-α, dθ/dt=v₁/R.

Cuando θ=α, el esquiador abandona el tercer tramo y entra en el cuarto.

Cuarto arco de circunferencia

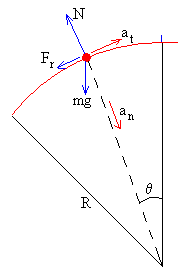
La ecuación del movimiento a lo largo de la dirección radial es

${\displaystyle mg\cos \theta -N=m{a}_n{a}_n=\frac{v^2}{R}}$

La ecuación del movimiento a lo largo de la dirección tangencial es

ma_t=mg·senθ-F_r  ya que θ es un ángulo negativo

Combinado ambas ecuaciones obtenemos las misma ecuación que en el primer arco. La velocidad se calcula mediante

${\displaystyle \frac{v^2}{Rg}=C\exp (2\mu \theta )+\frac{-6\mu ·\sin \theta -(2-4{\mu }^2)\cos \theta }{4{\mu }^2+1}}$   (1)

La constante C se determina a partir de las condiciones iniciales, para θ=-α, v=v₂, donde v₂ es la velocidad del esquiador al finalizar el tercer tramo.

Ecuación diferencial del movimiento:

Poniendo v=R·dθ/dt, obtenemos la ecuación diferencial del movimiento, la misma que para el primer arco

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{g}{R}(\sin \theta -\mu \cos \theta )+\mu {\left(\frac{d\theta }{dt}\right)}^2}$

que se resuelve por procedimientos numéricos con las condiciones iniciales t=t₂, θ=-α, dθ/dt=v₂/R.

Cuando θ=0, el esquiador abandona el valle y llega al final del puente.

Ejemplo

• Coeficiente de rozamiento μ=0.1
• Ángulo de cada uno de los cuatro arcos que forman el valle α=30º
• Velocidad inicial de los esquiadores al comienzo de la carrera v₀=5 m/s
• Longitud del puente d=10 m

Calculamos el radio R de los arcos

d=4·Rsenα,  R=5 m

Primer arco

Las condiciones iniciales son θ=0, v₀=5 m/s, calculamos la constante de integración C en la expresión (1).

$$\begin{gathered} {\displaystyle \frac{5^2}{5·9.8}=C\exp (2·0.1·0)+\frac{-6·0.1·\sin \text{0}-(2-4·{0.1}^2)\cos 0}{4·{0.1}^2+1} \\ C=2.395} \end{gathered}$$

Conocida la constante C, calculamos la velocidad del móvil al finalizar el primer arco θ=30º=π/6 rad

$$\begin{gathered} {\displaystyle \frac{v^2}{5·9.8}=2.395·\exp \left(2·0.1·\frac{\pi }{6}\right)+\frac{-6·0.1·\sin \text{(}\pi \text{/6)}-(2-4·{0.1}^2)\cos (\pi /6)}{4·{0.1}^2+1} \\ v=6.02\text{m/s}} \end{gathered}$$

Esta es la velocidad inicial cuando el móvil entra en el segundo arco y tercer arco.

Segundo y tercer arco

Las condiciones iniciales son θ=-π/6, v₁=6.02 m/s, calculamos la constante de integración C en la expresión (2).

$$\begin{gathered} {\displaystyle \frac{{6.02}^2}{5·9.8}=C\exp \left(-2·0.1·\frac{-\pi }{6}\right)+\frac{-6·0.1·\sin (-\pi /6)+(2-4·{0.1}^2)\cos (-\pi /6)}{4·{0.1}^2+1} \\ C=-1.064} \end{gathered}$$

Conocida la constante C, calculamos la velocidad del móvil al finalizar el tercer arco θ=π/6 rad

$$\begin{gathered} {\displaystyle \frac{v^2}{5·9.8}=-1.064\exp \left(-2·0.1·\frac{\pi }{6}\right)+\frac{-6·0.1·\sin (\pi /6)+(2-4·{0.1}^2)\cos (\pi /6)}{4·{0.1}^2+1} \\ v=4.34\text{m/s}} \end{gathered}$$

Esta es la velocidad inicial cuando el móvil entra en el cuarto arco.

Cuarto arco 

Las condiciones iniciales son θ=-π/6, v₁=4.34 m/s, calculamos la constante de integración C de la expresión (1).

$$\begin{gathered} {\displaystyle \frac{{4.34}^2}{5·9.8}=C·\exp \left(2·0.1·\frac{-\pi }{6}\right)+\frac{-6·0.1·\sin \text{(-}\pi \text{/6)}-(2-4·{0.1}^2)\cos (-\pi /6)}{4·{0.1}^2+1} \\ C=1.920} \end{gathered}$$

Conocida la constante C, calculamos la velocidad del móvil al finalizar el cuarto arco θ=0 rad

$$\begin{gathered} {\displaystyle \frac{v^2}{5·9.8}=1.920·\exp (2·0.1·0)+\frac{-6·0.1·\sin \text{0}-(2-4·{0.1}^2)\cos 0}{4·{0.1}^2+1} \\ v=1.31\text{ m/s}} \end{gathered}$$

Esta es la velocidad final del esquiador que atraviesa el valle. El programa interactivo, calcula numéricamente el tiempo que tarda el esquiador en atravesar el valle, 2.45 s.

Movimiento a lo largo del puente

La velocidad final del esquiador que cruza el puente es

v²=5²-2·0.1·9.8·10,  v=2.32 m/s

El tiempo que tarda en cruzar el puente es

v=5-0.1·9.8·t,  t=2.73 s

Actividades

Se introduce

• El coeficiente de rozamiento μ, en el control titulado Coef. rozamiento

• El ángulo α, de cada uno de los cuarto arcos que componen el valle, en el control titulado Ángulo del arco.

• La velocidad inicial v₀, que llevan los dos esquiadores al comenzar su carrera, en el control titulado V. inicial.

• La longitud d del puente se ha fijado en 10 m.

Se pulsa el botón titulado Nuevo

Se observa el puente en color azul, y el perfil del valle en color rojo formado por la unión de cuatro arcos.

Se dibuja las fuerzas sobre la partícula roja que cruza el valle

• El peso, mg

• La fuerza de rozamiento, F_r, cuya dirección es tangente a la trayectoria circular, y cuyo sentido es opuesto a la velocidad

• La reacción N de la superficie curva, que tiene dirección radial.

En la parte izquierda se realiza el balance energético de las dos partículas:

A la izquierda, la energía de la partícula de color rojo que atraviesa el valle

• La energía potencial en color azul, que es negativa
• La energía cinética en color rojo
• La energía total se señala mediante un rectángulo de color negro

A la derecha, la energía de la partícula de color azul que atraviesa el puente

• Su energía potencial no cambia, se toma como cero
• La energía cinética en color rojo, que es a su vez la energía total

Una línea horizontal de color negro señala la energía inicial de ambas partículas, observamos como la energía va disminuyendo a causa del trabajo de la fuerza de rozamiento.

En la parte inferior derecha, se proporcionan los datos del tiempo, posición horizontal de cada uno de los esquiadores en relación al principio del puente y de su velocidad.

Referencias

Hite G. E. The sled race. Am. J. Phys. 72 (8) August 2004, pp. 1055-1058