Sistema conservativo
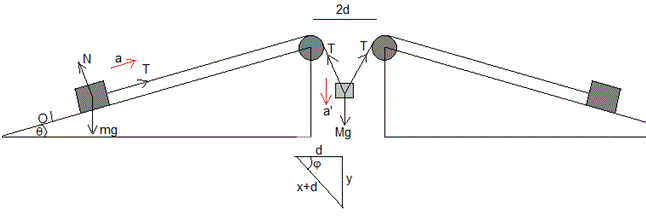
El sistema consiste en dos planos inclinados iguales, un ángulo θ. A lo largo de los planos deslizan dos cuerpos (carritos) de la misma masa m. Los dos cuerpos están unidos mediante cuerdas, que pasan por poleas de masa y radio despreciables, a un cuerpo de masa M (contrapeso) que se mueve verticalmente entre los dos planos inclinados que distan 2d.
Cinemática
La posición del carrito de masa m es x a lo largo del plano inclinado y la posición vertical del contrapeso de masa M es y. Ambas posiciones están relacionadas, tal como se aprecia en el triángulo rectángulo inferior.
Relación entre las posiciones
Las velocidades están relacionadas
Las aceleraciones están relacionadas
Dinámica
Las fuerzas sobre el cuerpo de masa m situado sobre el plano inclinado, son:
- El peso, mg
- La reacción del plano, N
- La tensión de la cuerda, T
Las fuerzas sobre el cuerpo de masa M que cuelga, son:
- El peso, Mg
- Las tensiones de las cuerdas izquierda y derecha, que son iguales, T
Equilibrio
El carrito está siempre en equlibrio en la dirección perpendicular al plano inclinado, N=mgcosθ
Cuando está en equilibrio en la dirección del plano inclinado, T=mgsinθ
El contrapeso, estará en equilibrio si
2Tsinφ=Mg
Dado que sinφ no puede ser mayor o igual que la unidad. Habrá equilibrio siempre que M≤2msinθ
Como cosφ=d/(x+d), obtenemos la posición xe de equilibrio del carrito sobre el plano inclinado.
Ecuaciones del movimiento
La ecuación del movimiento del cuerpo de masa m a lo largo del plano inclinado es
La ecuación del movimiento vertical del cuerpo de masa M es
Eliminamos la tensión T de la cuerda y relacionamos las dos aceleraciones (véase el apartado Cinemática)
Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, el cuerpo de masa m parte del reposo dx/dt=0, desde la posición x0
Conservación de la energía
- Cuando el contrapeso desciende una altura y, su energía potencial disminuye, Mgy
- Su energía cinética aumenta, M(dy/dt)2/2
- La energía cinética de los dos carritos aumenta, 2(m(dx/dt)2/2)=m(dx/dt)2
- Su energía potencial también se incrementa, 2(mgxsinθ)
Si los carritos parten del reposo desde la posición inicial x0 y el contrapeso parte de la posición inicial y0, la energía inicial es
Los carritos deslizan se encuentran en el instante t en la posición x y se mueven con velocidad dx/dt, mientras el contrapeso se encuentra en la posición y con velocidad dy/dt, el principio de conservación de la energía se escribe
Como las velocidades dx/dt y dy/dt están relaciondas
Velocidades
Representamos el cuadrado de la velocidad dx/dt para dos ángulos del plano inclinado θ=10.2° y 8°, tomando m/M=3, la separación entre los planos inclinados d=0.15 m, la posición de partida del carrito, en reposo, es x0=0.1 m
m=3; %cuerpo sobre plano inclinado
M=1; % cuerpo que cuelga
d=0.15; %distancia entre planos inclinados
x0=0.1;
hold on
for th=[8,10.2]*pi/180 %ángulo de los planos inclinados
E0=-M*9.8*sqrt(x0^2+2*d*x0)+2*m*9.8*x0*sin(th);
v2=@(x) 2*(x.^2+2*d*x).*(E0+M*9.8*sqrt(x.^2+2*d*x)-
2*m*9.8*x*sin(th))./((M*(x+d).^2+2*m*(x.^2+2*d*x)));
fplot(v2,[x0,1],'displayName',num2str(th*180/pi))
end
hold off
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('v^2')
grid on
title('Velocidad')
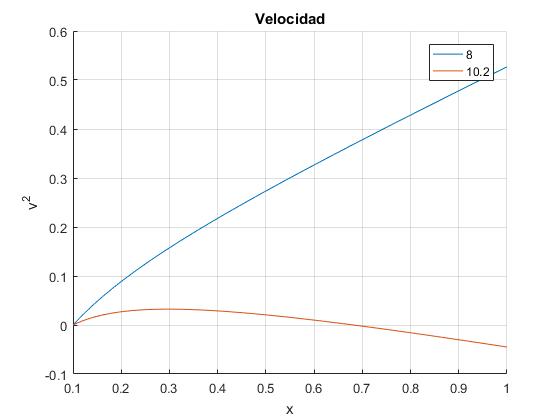
Para θ=8°, la velocidad del carrito crece indefindamente. Para θ=10.2° la velocidad crece, pasa por un máximo en x≈0.3 m y luego, decrece hasta hacerse cero en x≈0.7 m
Aceleraciones
Sustituimos dx/dt en la ecuación diferencial del movimiento, para expresar la aceleración en función de la posición x
Representamos la aceleración dx/dt de los carritos y la aceleración dy/dt del contrapeso para m/M=3, el ángulo del plano inclinado inclinado es θ=10°, la separación entre los planos inclinados d=0.15 m. La posición de partida del carrito en reposo, es muy próxima al origen x0=0.001 m
m=3; %cuerpo sobre plano inclinado
M=1; % cuerpo que cuelga
d=0.15; %distancia entre planos inclinados
th=10*pi/180; %ángulo de los planos inclinados
x0=0.001; %posición de partida
E0=-M*9.8*sqrt(x0^2+2*d*x0)+2*m*9.8*x0*sin(th);
v2=@(x) 2*(x.^2+2*d*x).*(E0+M*9.8*sqrt(x.^2+2*d*x)-
2*m*9.8*x*sin(th))./((M*(x+d).^2+2*m*(x.^2+2*d*x)));
a=@(x) (M*d^2*v2(x)./(x.^2+2*d*x).^(3/2)-2*m*9.8*sin(th)*
sqrt(x.^2+2*d*x)./(x+d)+M*9.8)./(2*m*sqrt(x.^2+2*d*x)./(x+d)+M*(x+d).
/sqrt(x.^2+2*d*x));
ap=@(x) (x+d).*a(x)./sqrt(x.^2+2*d*x)-d^2*v2(x)./(x.^2+2*d*x).^(3/2);
hold on
fplot(a,[x0,0.2])
fplot(ap,[x0,0.2])
hold off
xlabel('x')
ylabel('a')
legend('a','a_p')
grid on
title('aceleraciones')
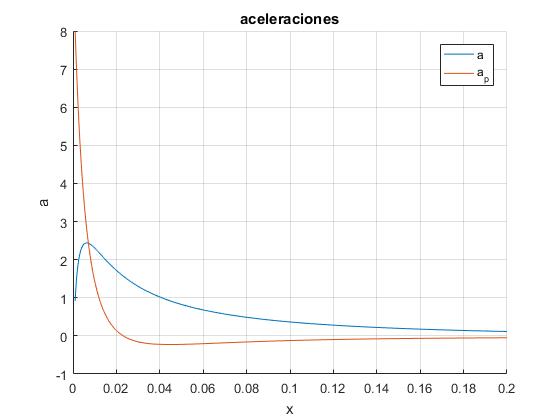
La aceleración a de los carritos tiende a cero y la aceleración del contrapeso ap tiende a g cuando nos aproximamos al origen x→0. Tal como se aprecia en la siguiente figura, cuando x=0, las cuerdas que sujetan al contrapeso son horizontales. La aceleración de este cuerpo es la gravedad y nula la aceleración de los carritos

Angulo límite
Cuando x o y se hacen grandes, el ángulo φ→π/2, sinφ=y/(x+d) →1, la aceleración dx/dt tiende a cero y la velocidad tiende hacia un valor constante cuando
Para m/M=3, el ángulo límite θ=9.59°
Cuando se cumple esta condición, M=2msinθ, escribimos el cuadrado de la velocidad (dx/dt)2 de la forma
Cuando x o y se hacen grandes, el ángulo φ→π/2, sinφ=y/(x+d) →1, el cuadrado de la velocidad tiende a
m=3; %cuerpo sobre plano inclinado
M=1; % cuerpo que cuelga
d=0.15; %distancia entre planos inclinados
x0=0.1;
th=asin(M/(2*m)); %ángulo del plano inclinado
E0=-M*9.8*sqrt(x0^2+2*d*x0)+2*m*9.8*x0*sin(th);
v=@(x) sqrt(2*(x.^2+2*d*x).*(E0+M*9.8*sqrt(x.^2+2*d*x)-
2*m*9.8*x*sin(th))./((M*(x+d).^2+2*m*(x.^2+2*d*x))));
fplot(v,[x0,5])
xlabel('x')
ylabel('v')
grid on
title('Velocidad')
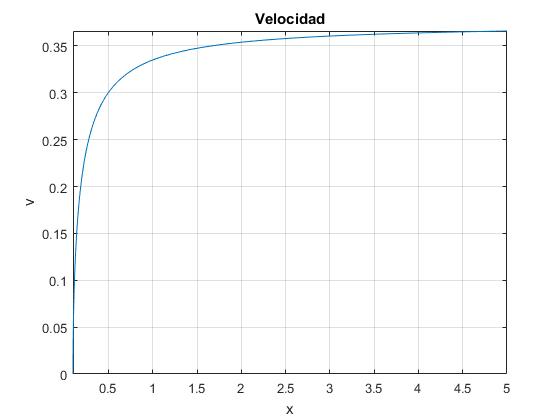
El ángulo del plano inclinado θ y la velocidad límite constante son
>> th*180/pi ans = 9.5941 >> sqrt(2*(E0+2*m*9.8*d*sin(th))/(M+2*m)) ans = 0.3742
Ejemplos
Resolvemos la ecuación diferencial del movimiento para m/M=3, el ángulo del plano inclinado inclinado es θ=10°, la separación entre los planos inclinados d=0.15 m. La posición de partida del carrito, en reposo, es x0=0.1 m
Dado que 2·3·sin10°>1, tendremos un sistema oscilante alrededor de la posición de equilibrio xe=38.4 cm. Aplicamos el principio de conservación de la energía para calcular la velocidad máxima, ve cuando pasa por dicha posición
Elaboramos un script para representar la velocidad dx/dt en función de la posición x del carrito
m=3; %cuerpo sobre plano inclinado
M=1; % cuerpo que cuelga
d=0.15; %distancia entre planos inclinados
th=10*pi/180; %ángulo de los planos inclinados
f=@(t,x) [x(2); (M*d^2*x(2)^2/(x(1)^2+2*d*x(1))^(3/2)-
2*m*9.8*sin(th)*sqrt(x(1)^2+2*d*x(1))/(x(1)+d)+M*9.8)
/(2*m*sqrt(x(1)^2+2*d*x(1))/(x(1)+d)+M*(x(1)+d)/sqrt(x(1)^2+2*d*x(1)))];
[t,x]=ode45(f,[0,15],[0.1,0]);
plot(x(:,1),x(:,2))
%equilibrio
if M<=2*m*sin(th)
xe=d*(2*m*sin(th)/sqrt(4*m^2*sin(th)^2-M^2)-1);
ye=sqrt(xe^2+2*d*xe);
x0=0.1;
y0=sqrt(x0^2+2*d*x0);
E0=(-M*y0+2*m*x0*sin(th))*9.8; %energía inicial
%velocidad máxima
ve=sqrt((E0+M*9.8*ye-2*m*9.8*xe*sin(th))/((M/2)*((xe+d)/ye)^2+m));
line([xe,xe],[-ve,ve],'lineStyle','--')
end
grid on
xlabel('x')
ylabel('v')
title('posición-velocidad')
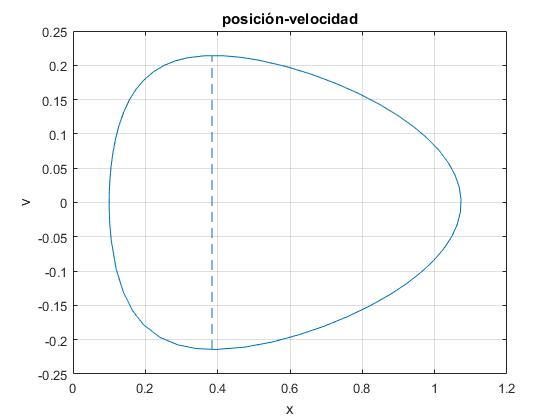
La posición de equilibrio del carrito xe y la velocidad cuando pasa por esta posición son
>> xe xe = 0.3844 >> ve ve = 0.2143
El procedimiento ode45 nos proporciona la posición x y la velocidad dx/dt del carrito en función del tiempo t, comprobamos el principio de conservación de la energía
>> -M*9.8*sqrt(x(:,1).^2+2*d*x(:,1))+ (M/2)*(x(:,2).^2).*(x(:,1)+d).^2./(x(:,1).^2+ 2*d*x(:,1))+m*(x(:,2).^2)+2*m*9.8*x(:,1)*sin(th) ans = -0.9389 -0.9389 ..... -0.9390 -0.9390 -0.9390
Resolvemos la ecuación diferencial del movimiento para m/M=3, la separación entre los planos inclinados d=0.15 m. La posición de partida del carrito, en reposo, es x0=0.05 m
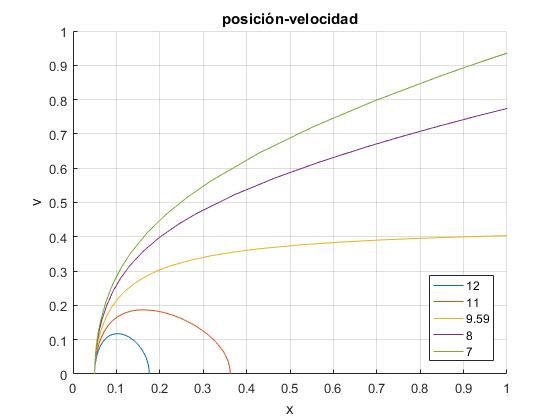
Representamos la velocidad del carrito dx/dt en función de la posición x, para los siguientes ángulos del plano inclinado:
- 11° y 12°, en ambos casos se cumple que M≤2msinθ, el sistema oscila alrededor de la posición de equilibrio
- 9.59°, se cumple que M=2msinθ, situación límite. Cuando x se hace grande la aceleración tiende a cero y la velocidad dx/dt tiende hacia un valor límite constante
- 8° y 7°, se cumple que M>2msinθ, no hay posición de equilibrio
Definimos una función para que el procedimiento ode45 se detenga cuando x>1, o cuando la velocidad dx/dt se hace cero
function [value,isterminal,direction]=stop_conservativo(t,x)
value=[x(2), x(1)-1];
isterminal=[1,1]; %1 detiene la integración
direction=[-1,1]; % 1 crece, -1 decrece, 0 no importa
end
Elaboramos un script para representar las trayectorias en el espacio de las fases
m=3; %cuerpo sobre plano inclinado
M=1; % cuerpo que cuelga
d=0.15; %distancia entre planos inclinados
hold on
opts=odeset('events',@stop_conservativo);
for th=[12,11,9.59,8,7]*pi/180
f=@(t,x) [x(2); (M*d^2*x(2)^2/(x(1)^2+2*d*x(1))^(3/2)-2*m*9.8*sin(th)*
sqrt(x(1)^2+2*d*x(1))/(x(1)+d)+M*9.8)/(2*m*sqrt(x(1)^2+2*d*x(1))
/(x(1)+d)+M*(x(1)+d)/sqrt(x(1)^2+2*d*x(1)))];
[t,x]=ode45(f,[0,10],[0.05,0],opts);
plot(x(:,1),x(:,2),'displayName',num2str(th*180/pi))
end
hold off
grid on
legend('-DynamicLegend','location','southeast')
xlabel('x')
ylabel('v')
title('posición-velocidad')
Actividades
Se introduce
- La masa m de cada uno de los carritos que deslizan a lo largo del plano inclinado, en el control titulado Masa m (kg)
- La masa del contrapeso que se mueve verticalmente, se ha fijado en M=1 kg
- El ángulo θ de los planos inclinados, en el control titulado Angulo
- Se ha fijado la distancia entre los planos inclinados, d=0.15 m
- Se ha fijado la posición de partida, en reposo, de los carritos en x0=0.1 m
Se muestra el movimiento de los cuerpos y se proporcionan los datos del
- Tiempo, t
- Posición de los carritos, x
- Velocidad de los carritos, dx/dt
- Posición del contrapeso, y
- Velocidad del contrapeso, dy/dt
El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente
donde E es la energía del sistema en cualquier instante t y E0 es la energía inicial del sistema.
Este valor se proporciona en caracteres de color rojo en la parte inferior izquierda. Su valor debe ser siempre cero, o un valor muy pequeño lo que indica que la energía del sistema permanece constante y el programa realiza los cálculos correctamente.
Para x=0, y=0, varios términos de la ecuación diferencial del movimiento se hacen infinitos, para evitarlo, la energía del sistema tiene que ser negativa, E0<0. En el caso de que fuese positiva o nula, un mensaje nos lo advierte
Referencias
K. Mita, W. Shirley, C. R. Chang. An experiment with two air tracks. Am. J. Phys. 54 (5) May 1986, pp. 428-432

