Consideremos dos bloques de masas m₁ y m₂ unidos por una cuerda inextensible y sin masa de longitud 2d que pasa por una polea ideal. El primer bloque desliza sobre un plano horizontal y el segundo se deja caer cuando la cuerda está horizontal tal como se muestra en la figura. En la segunda, se muestra el sistema en el instante t. A medida que el bloque de masa m₂ cae, arrastra al bloque de masa m₁. En esta figura se muestran las fuerzas sobre cada uno de los bloques. Como el bloque m₁ desliza sin rozamiento se ha omitido el peso y la reacción del plano horizontal

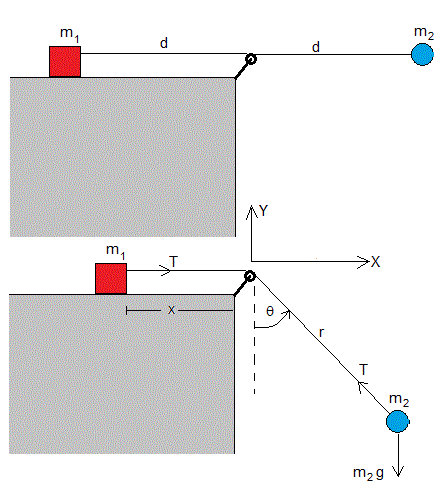
La posición del bloque m₁ es x, la posición del bloque m₂ en coordenadas es r y θ. Se cumple que -x+r=2d.

Sobre el primer bloque actúa la tensión T de la cuerda. La ecuación del movimiento es

${\displaystyle m_1\frac{d^{2}x}{d{t}^2}=T}$

Para describir el movimiento de m₂ es mejor expresar la velocidad y aceleración en coordenadas polares, véase al final de la página

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\hfill \\ \overrightarrow{a}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)\widehat{\theta }\hfill \end{array}}$

Sobre el segundo cuerpo actúan dos fuerzas, el peso m₂g y la tensión T de la cuerda. Sustituimos el peso por la acción simultánea de sus componentes y escribimos las ecuaciones del movimiento

${\displaystyle \begin{array}{l}{m}_2\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=m_{2}g\cos \theta -T\\ m_2\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)=-m_{2}g\sin \theta \end{array}}$

Tenemos tres ecuaciones del movimiento. Eliminamos la tensión T de la cuerda y escribimos la posición x del primer bloque en términos de la distancia radial r del segundo, sabiendo que -x+r=2d.

${\displaystyle \begin{array}{l}\frac{d^{2}r}{d{t}^2}=\frac{m_2}{m_1+m_2}\left(g\cos \theta +r{\left(\frac{d\theta }{dt}\right)}^2\right)\\ \frac{d^2\theta }{d{t}^2}=-\frac{1}{r}\left(g\sin \theta +2\frac{d\theta }{dt}\frac{dr}{dt}\right)\end{array}}$

Resolvemos el sistema de dos ecuaciones diferenciales por procedimientos numéricos con las siguientes condiciones iniciales

${\displaystyle t=0\{\begin{array}{l}r=d\\ \frac{dr}{dt}=0\end{array}\{\begin{array}{l}\theta =\pi /2\\ \frac{d\theta }{dt}=0\end{array}}$

Energía del sistema

Estableciendo el nivel cero de energía potencial en la posición incial cuando la cuerda está horizontal. La energía inicial es E₀=0. La energía al cabo de un tiempo t es

${\displaystyle \begin{array}{l}E=\frac{1}{2}{m}_1{\left(\frac{dx}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(r\frac{d\theta }{dt}\right)}^2-m_{2}gr\cos \theta \\ E=\frac{1}{2}(m_1+m_2){\left(\frac{dr}{dt}\right)}^2+\frac{1}{2}{m}_2{\left(r\frac{d\theta }{dt}\right)}^2-m_{2}gr\cos \theta \end{array}}$

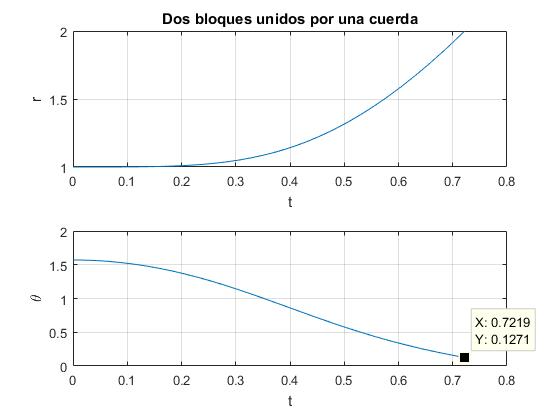
Sea la longitud de la cuerda 2d=2, y la relación m=m₁/m₂=1, las masas iguales. Resolvemos el sistema de ecuaciones diferenciales con las condiciones iniciales señaladas. Vemos que el primer bloque llega al final del plano horizontal x=0 en el instante t=0.72, cuando la cuerda que sujeta el segundo bloque hace un ángulo de con la pared vertical de 0.1271·180/pi=7.28°

Se comprueba que la energía total E (línea comentada con %) es próxima a cero.

m=1; %cociente m1/m2
x0=[1,0,pi/2,0]; %[r,dr/dt,theta,dtheta/dt]
tspan=[0,1];

fg=@(t,x)[x(2);(x(1)*x(4)^2+9.8*cos(x(3)))/(1+m); 
x(4);-(2*x(2)*x(4)+9.8*sin(x(3)))/x(1)];
opts=odeset('events',@stop_bloques);
[t,x]=ode45(fg,tspan,x0,opts);
%E=(m+1)*x(:,2).^2/2+(x(:,1).^2).*(x(:,4).^2)/2
-9.8*x(:,1).*cos(x(:,3));%energía
subplot(2,1,1)
plot(t,x(:,1))  %t,r
grid on
xlabel('t')
ylabel('r')
title('Dos bloques unidos por una cuerda')
subplot(2,1,2)
plot(t,x(:,3)) %t, theta
grid on
xlabel('t')
ylabel('\theta')

Esta función detiene el proceso de integración cuando el primer bloque se encuentra en x=2-r=0, o cuando el segundo bloque impacta en la pared vertical θ=0.

function [detect,stopin,direction]=stop_bloques(~,x)
    if x(3)>(2-x(1))   
        detect=2-x(1); %2-r
    else
        detect=x(3); %theta
    end
    stopin=1; 
    direction=-1; 
end

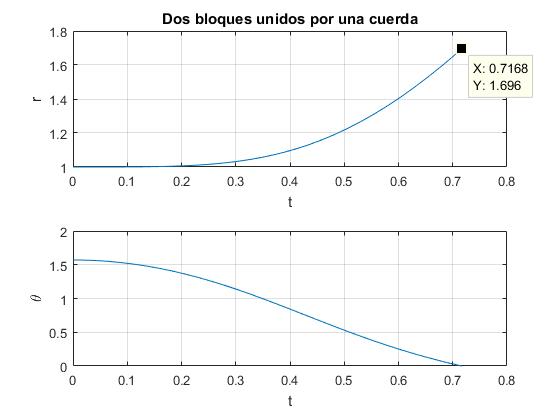
Modificamos la relación m=m₁/m₂=2. Resolvemos el sistema de ecuaciones diferenciales. El segundo bloque impacta con la pared vertical θ=0, en el instante t= 0.7168 cuando el primer bloque se encuentra en la posición x=2-1.696=0.3040

Actividades

Se introduce

• El cociente entre masas m₁/m₂
• Se ha fijado la longitud 2d de la cuerda en 2

Se pulsa el botón titulado Nuevo

Observamos el movimiento de los bloques que se detiene cuando el primer bloque llega al final del plano horizontal x=0 o bien, cuando el segundo bloque choca con la pared vertical θ=0

El programa interactivo calcula la energía del sistema total en cada instante, que debería ser cero, para verificar que el procedimiento numérico empleado para resolver el sistema de dos ecuaciones diferenciales calcula correctamente las posiciones y velocidades de los cuerpos

Referencias

Norman Paris, Michael L. Broide. Unraveling a classical mechanics brain twister. Am. J. Phys. 79 (12) December 2011, pp. 1250-1254

Coordenadas polares

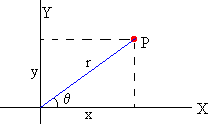
La posición de una partícula es (x, y) en coordenadas rectangulares y (r, θ) en coordenadas polares. La relación es

x=r·cosθ, y=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

${\displaystyle \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{d\left(r·\widehat{r}\right)}{dt}=\widehat{r}\frac{dr}{dt}+r\frac{d\widehat{r}}{dt}}$

Calculamos las componentes rectangulares de los vectores unitarios

${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\sin \theta \hfill \\ \widehat{\theta }=-\widehat{i}\sin \theta +\widehat{j}\cos \theta \hfill \end{array}}$

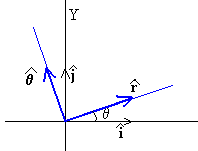
vemos que

${\displaystyle \begin{array}{l}\frac{d\widehat{r}}{dt}=(-\widehat{i}\sin \theta +\widehat{j}\cos \theta )\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\hfill \\ \frac{d\widehat{\theta }}{dt}=(-\widehat{i}\cos \theta -\widehat{j}\sin \theta )\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\hfill \end{array}}$

Las expresión del vector velocidad en coordenadas polares es

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

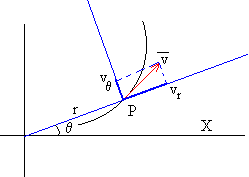
Las expresión del vector aceleración es:

${\displaystyle \begin{array}{l}\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\hfill \\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+\left(r\frac{d^2\theta }{d{t}^2}+\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }-r{\left(\frac{d\theta }{dt}\right)}^2\widehat{r}=\hfill \\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\hfill \end{array}}$