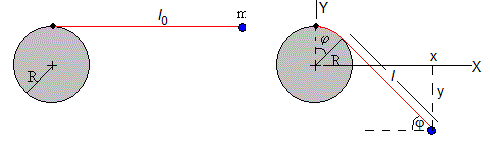
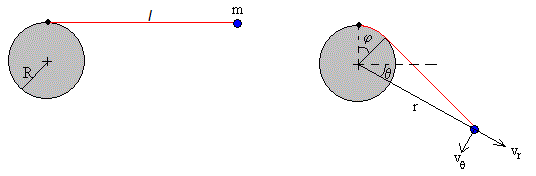
Cuando la partícula de masa m cae, en el instante t la parte de la cuerda que está enrollada en el cilindro es la longitud Rφ del arco de una circunferencia de radio R. Describiremos el movimiento de la partícula en términos del ángulo φ.

Posición, velocidad y aceleración de la partícula

La posición de la partícula en el Sistema de Referencia de la figura es

${\displaystyle \{\begin{array}{l}x=R\sin \phi +l\cos \phi =R\sin \phi +\left(l_0-R\phi \right)\cos \phi \\ y=R\cos \phi -l\sin \phi =R\cos \phi -\left(l_0-R\phi \right)\sin \phi \end{array}}$

Donde l=l₀-Rφ

Derivamos con respecto del tiempo para obtener las componentes de la velocidad

${\displaystyle \begin{array}{l}\{\begin{array}{l}\frac{dx}{dt}=\left(R\cos \phi -l\sin \phi \right)\frac{d\phi }{dt}+\cos \phi \frac{dl}{dt}=\left(R\cos \phi -l\sin \phi \right)\frac{d\phi }{dt}-R\cos \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=\left(-R\sin \phi -l\cos \phi \right)\frac{d\phi }{dt}-\sin \phi \frac{dl}{dt}=\left(-R\sin \phi -l\cos \phi \right)\frac{d\phi }{dt}+R\sin \phi \frac{d\phi }{dt}\end{array}\\ \{\begin{array}{l}\frac{dx}{dt}=-\left(l_0-R\phi \right)\sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=-\left(l_0-R\phi \right)\cos \phi \frac{d\phi }{dt}\end{array}\end{array}}$

Derivamos respecto del tiempo para obtener las componentes de la aceleración

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\left(R\sin \phi -\left(l_0-R\phi \right)\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2-\left(l_0-R\phi \right)\sin \phi \frac{d^2\phi }{d{t}^2}\\ \frac{d^{2}y}{d{t}^2}=\left(R\cos \phi +\left(l_0-R\phi \right)\sin \phi \right){\left(\frac{d\phi }{dt}\right)}^2-\left(l_0-R\phi \right)\cos \phi \frac{d^2\phi }{d{t}^2}\end{array}}$

Ecuación del movimiento

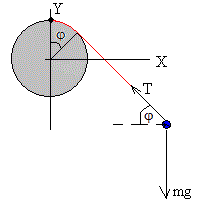
Las fuerzas que actúan sobre la partícula son:

• El peso, mg
• La tensión de la cuerda, T

${\displaystyle \{\begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-T\cos \phi \\ m\frac{d^{2}y}{d{t}^2}=T\sin \phi -mg\end{array}}$

Eliminamos la tensión T en el sistema de dos ecuaciones, multiplicando la primera por sinφ, la segunda por cosφ y sumando

${\displaystyle (l_0-R\phi )\frac{d^2\phi }{d{t}^2}=g\cos \phi +R{\left(\frac{d\phi }{dt}\right)}^2}$

Despejamos la tensión T/m de la cuerda

${\displaystyle \frac{T}{m}=g\sin \phi +\left(l_0-R\phi \right){\left(\frac{d\phi }{dt}\right)}^2}$

Conservación de la energía

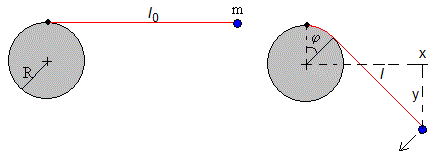
Ponemos el nivel cero de energía potencial en el origen.

La energía inicial de la partícula es E₀=mgR

La energía de la partícula en cualquier instante es

${\displaystyle E=\frac{1}{2}m{l}^2{\left(\frac{d\phi }{dt}\right)}^2+mgy=\frac{1}{2}m{\left(l_0-R\phi \right)}^2{\left(\frac{d\phi }{dt}\right)}^2+mg\left(R\cos \phi -\left(l_0-R\phi \right)\sin \phi \right)}$

La energía permanece constante, E=E₀=mgR

${\displaystyle {\left(\frac{d\phi }{dt}\right)}^2=2g\frac{R-R\cos \phi +\left(l_0-R\phi \right)\sin \phi }{{\left(l_0-R\phi \right)}^2}}$

Tensión de la cuerda

La tensión T de la cuerda es una función del ángulo φ.

${\displaystyle \frac{T}{m}=g\frac{2R-2R\cos \phi +3\left(l_0-R\phi \right)\sin \phi }{l_0-R\phi }}$

La tensión de la cuerda se anula cuando

${\displaystyle \begin{array}{l}2R-2R\cos \phi +3\left(l_0-R\phi \right)\sin \phi =0\\ \frac{3}{2}\left(\phi -\frac{l_0}{R}\right)=\tan \frac{\phi }{2}\end{array}}$

Se resuelve por procedimientos numéricos esta ecuación trascendente.

La cuerda alcanzará la tensión nula siempre que no se enrolle completamente, es decir, Rφ<l₀. El primer término de la igualdad ha de ser negativo, por lo que se tiene que igualar a la rama negativa de tan(φ/2), es decir, el ángulo 180<φ<360, tal como se aprecia en la figura.

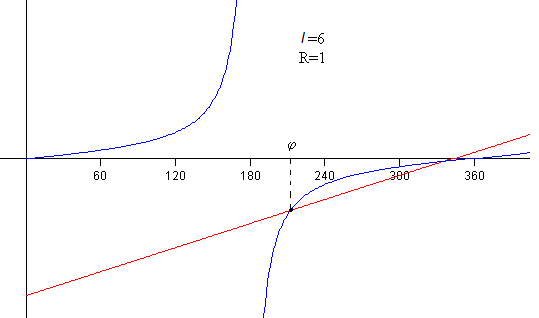
En la figura, representamos la recta y=(3/2)(φ-l₀/R) y la función y=tan(φ/2) para l₀=6 m y R=1 m.

Denominamos longitud crítica de la cuerda l_c a aquella que se enrolla completamente en el cilindro y a la vez, alcanza la tensión cero en el punto de contacto de la partícula.

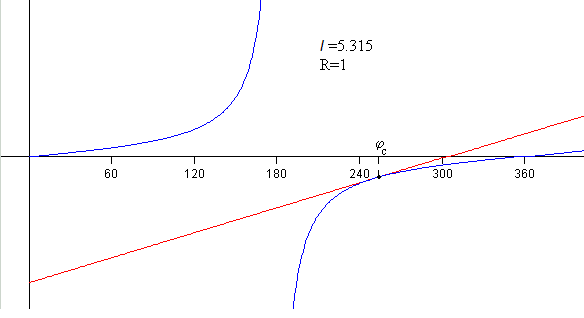
Como vemos en la figura, la recta y=(3/2)(φ-l₀/R) y la función y=tan(φ/2) se cortan en el punto de tangencia. En el punto de corte la pendiente de la función es 3/2.

${\displaystyle \frac{3}{2}=\frac{1}{2}\frac{1}{{\cos }^2(\phi /2)}{\phi }_c=250.5º=4.372\text{rad}}$

Introducimos el valor del ángulo φ en la ecuación trascendente y despejamos el cociente l/R.

${\displaystyle \frac{l_c}{R}={\phi }_c-\frac{2}{3}\tan \left(\frac{{\phi }_c}{2}\right)\frac{l_c}{R}=5.315}$

• Cuando la longitud l₀ de la cuerda es menor que l_c la cuerda se enrolla completamente en el cilindro
• Cuando la longitud l₀ de la cuerda es mayor que l_c la cuerda alcanza la tensión T=0

Se utiliza la función buscar_intervalos, para encontrar el primer intervalo en el que la función g(x) cambia de signo. La función MATLAB fzero, encuentra el ángulo límite en dicho intervalo.

Definimos la función stop_enrolla, para que el procedimiento ode45 de integración de la ecuación diferencial termine cuando se alcanza el ángulo límite

function enrolla
    L=6; %longitud de la cuerda
    R=1; %radio
    %calcula el ángulo límite, T=0
    if L>5.315
        g=@(x) 3*(L-x)/2+tan(x/2);
        xb=buscar_intervalos(g,pi+0.1,2*pi,50);
        aLimite=fzero(g,[xb(1,1),xb(1,2)]);
    end
    
    %resuelve la ecuación diferencial
    f=@(t,x) [x(2); (9.8*cos(x(1))/R+x(2)^2)*R/(L-x(1))]; 
    opts=odeset('events',@(t,x) stop_enrolla(t,x,aLimite));
    [~,x]=ode45(f,[0,3],[0,0],opts);
    xp=R*sin(x(:,1))+(L-R*x(:,1)).*cos(x(:,1));
    yp=R*cos(x(:,1))-(L-R*x(:,1)).*sin(x(:,1));
    hold on
    %dibuja el cilindro
    z=0:pi/40:2*pi;
    fill(R*sin(z),R*cos(z),'g')
    %dibuja la trayectoria de la partícula
    plot(xp,yp)
    hold off
    grid on
    axis equal
    xlabel('x')
    ylabel('y');
    title('Cuerda que se enrolla')

    function xb = buscar_intervalos(f,a,b,n)
        x = linspace(a,b,n);
        j = 0; 
        xb=[];
        for i = 1:length(x)-1
            if sign(f(x(i))) ~= sign(f(x(i+1))) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end

    function [value,isterminal,direction]=stop_enrolla(~,x,xFin)
        value=x(1)-xFin; 
        isterminal=1;
        direction=0; 
    end
    
end

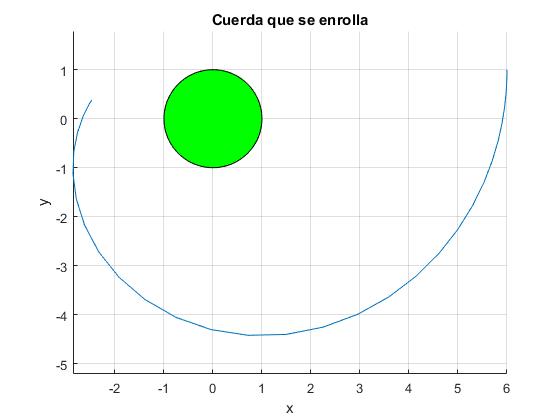
Comprobamos la conservación de la energía. La energía inicial es mgR

>> E=((L-R*x(:,1)).^2).*x(:,2).^2/2-9.8*((L-R*x(:,1)).*
sin(x(:,1))-R*cos(x(:,1)))
E =    9.8000
       9.8000
       ......
       9.7960
       9.7960

Tiro parabólico

Cuando la cuerda alcanza la tensión cero, supondremos que la partícula se mueve bajo la acción del peso, describiendo un tiro parabólico.

Se calcula el ángulo límite φ cuando la tensión es nula. La posición inicial x₀, y₀ de la partícula en ese instante es.

${\displaystyle \{\begin{array}{l}{x}_0=R\sin \phi +\left(l_0-R\phi \right)\cos \phi \\ y_0=R\cos \phi -\left(l_0-R\phi \right)\sin \phi \end{array}}$

Se calculan las componentes de la velocidad en dicho instante

${\displaystyle \begin{array}{l}{v}_{0x}=-(l_0-R\phi )\frac{d\phi }{dt}\sin \phi \hfill \\ v_{0y}=-(l_0-R\phi )\frac{d\phi }{dt}\cos \phi \hfill \end{array}}$

Las ecuaciones del movimiento de la partícula bajo la acción de su propio peso son:

${\displaystyle \begin{array}{l}x=x_0+v_{0x}t\\ y=y_0+v_{0y}t+\frac{1}{2}(-g)t^2\end{array}}$

Actividades

Se introduce

• La longitud l₀ de la cuerda, en el control titulado Longitud cuerda
• Se ha fijado el radio del cilindro en R=1 m

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la partícula hasta que:

• la cuerda se enrolla completamente en el cilindro
• la cuerda alcanza la tensión cero.

En el segundo caso, a partir de dicho instante, la partícula descibe un tiro parabólico

El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía en cualquier instante t y E₀=mgR es la energía inicial.

Deducción alternativa en coordenadas polares

Para describir el movimiento de la partícula adoptamos el sistema de referencia que se muestra en la figura

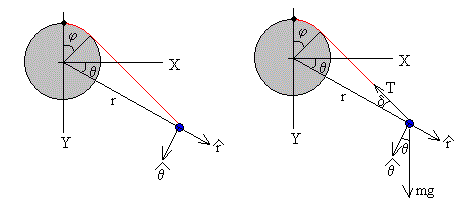
Expresamos la velocidad y aceleración en coordenadas polares, véase el final de la página Movimiento de dos bloques atados por una cuerda

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }\hfill \\ \overrightarrow{a}=\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{d\theta }{dt}\frac{dr}{dt}\right)\widehat{\theta }\hfill \end{array}}$

Ecuaciones de la dinámica

Las fuerzas que actúan sobre la partícula son:

• El peso, mg
• La tensión de la cuerda, T

Las ecuaciones del movimiento en la dirección radial $\widehat{r}$ y en la dirección $\widehat{\theta }$ son, respectivamente

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=mg\sin \theta -T\cos \delta \\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=mg\cos \theta -T\sin \delta \end{array}}$

Donde sinδ=R/r y cosδ=(l-Rφ)/r

Despejamos la tensión T de la segunda ecuación y la sustituimos en la primera

${\displaystyle \begin{array}{l}\frac{T}{m}=\frac{r}{R}\left\{g\cos \theta -\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\right\}\\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=g\sin \theta -\frac{r}{R}\left\{g\cos \theta -\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\right\}\frac{(l-R\phi )}{r}\end{array}}$

Esta es la ecuación diferencial del movimiento de la partícula en términos de r y θ  y el ángulo φ que como veremos se simplifica notablemente al expresarla únicamente en términos de la variable φ.

El arduo trabajo algebraico consiste en expresar r y θ y sus derivadas en términos del ángulo φ y sus derivadas.

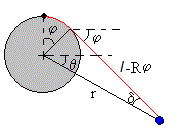
Como vemos en la figura

${\displaystyle \begin{array}{l}\{\begin{array}{l}r\sin \theta =(l-R\phi )\sin \phi -R\cos \phi \\ r\cos \theta =(l-R\phi )\cos \phi +R\sin \phi \end{array}\\ \tan \theta =\frac{(l-R\phi )\tan \phi -R}{(l-R\phi )+R\tan \phi }{r}^2={\left(l-R\phi \right)}^2+R^2\end{array}}$

Expresamos la derivada con respecto del tiempo t de r en términos de φ y su derivada.

${\displaystyle r\frac{dr}{dt}=-R(l-R\phi )\frac{d\phi }{dt}}$

Expresamos la derivada con respecto del tiempo t de θ en términos de φ y su derivada.

${\displaystyle \frac{1}{{\cos }^2\theta }\frac{d\theta }{dt}=\frac{\left(-R\tan \phi +(l-R\phi )\frac{1}{{\cos }^2\phi }\right)\left(l-R\phi +R\tan \phi \right)-\left(-R+\frac{R}{{\cos }^2\phi }\right)\left((l-R\phi )\tan \phi -R\right)}{{\left(l-R\phi +R\tan \phi \right)}^2}\frac{d\phi }{dt}}$

Teniendo en cuenta que 1/cos²θ=1+tan²θ, llegamos a la expresión

${\displaystyle r^2\frac{d\theta }{dt}={(l-R\phi )}^2\frac{d\phi }{dt}}$

A continuación, las derivadas segundas

${\displaystyle \begin{array}{l}r\frac{d^{2}r}{d{t}^2}=-R(l-R\phi )\frac{d^2\phi }{d{t}^2}+\frac{R^4}{r^2}{\left(\frac{d\phi }{dt}\right)}^2\\ r^2\frac{d^2\theta }{d{t}^2}={\left(l-R\phi \right)}^2\frac{d^2\phi }{d{t}^2}-\frac{2R^3}{r^2}\left(l-R\phi \right){\left(\frac{d\phi }{dt}\right)}^2\end{array}}$

Las componentes de la aceleración

${\displaystyle \begin{array}{l}\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=-\frac{R}{r}(l-R\phi )\frac{d^2\phi }{d{t}^2}+\frac{1}{r}\left(R^2-{\left(l-R\phi \right)}^2\right){\left(\frac{d\phi }{dt}\right)}^2\\ \left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=\frac{{\left(l-R\phi \right)}^2}{r}\frac{d^2\phi }{d{t}^2}-\frac{2R}{r}(l-R\phi ){\left(\frac{d\phi }{dt}\right)}^2\end{array}}$

Finalmente, expresamos la tensión de la cuerda y la ecuación del movimiento en términos del ángulo φ y sus derivadas.

${\displaystyle \begin{array}{l}\frac{T}{m}=g\sin \phi +(l-R\phi ){\left(\frac{d\phi }{dt}\right)}^2\\ \frac{d^2\phi }{d{t}^2}=\frac{R}{(l-R\phi )}\left(\frac{g}{R}\cos \phi +{\left(\frac{d\phi }{dt}\right)}^2\right)\end{array}}$

Resolvemos la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, φ=0, dφ/dt=0.

Una vez que conocemos el ángulo φ en función del tiempo, las coordenadas polares r y θ de la partícula se calculan del siguiente modo.

${\displaystyle \theta =\arctan \left(\frac{(l-R\phi )\sin \phi -R\cos \phi }{(l-R\phi )\cos \phi +R\sin \phi }\right)r=\sqrt{{\left(l-R\phi \right)}^2+R^2}}$

A continuación, la abscisa x y la ordenada y de la partícula

x=r·cosθ
y=r·sinθ

Conservación de la energía

Ponemos el nivel cero de energía potencial en el origen.

La energía inicial de la partícula es E_i=mgR

La energía final de la partícula es

${\displaystyle \begin{array}{l}{E}_f=\frac{1}{2}m\left(v_r^2+v_{\theta }^2\right)-mgr\sin \theta \\ E_f=\frac{1}{2}m\left({\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2\right)-mgr\sin \theta \end{array}}$

Expresamos r, θ y sus derivadas en términos de φ y sus derivadas

${\displaystyle \begin{array}{l}gR=\frac{{\left(l-R\phi \right)}^2}{2}{\left(\frac{d\phi }{dt}\right)}^2-g\left((l-R\phi )\sin \phi -R\cos \phi \right)\\ {\left(\frac{d\phi }{dt}\right)}^2=\frac{2g\left(R+(l-R\phi )\sin \phi -R\cos \phi \right)}{{\left(l-R\phi \right)}^2}\end{array}}$

function enrolla_1
    L=6; %longitud de la cuerda
    R=1; %Radio
    %calcula el ángulo límite
    if L>5.315
        g=@(x) 3*(L-x)/2+tan(x/2);
        xb=buscar_intervalos(g,pi+0.1,2*pi,50);
        aLimite=fzero(g,[xb(1,1),xb(1,2)]);
    end
    
    %resuelve la ecuación diferencial
    f=@(t,x) [x(2); (9.8*cos(x(1))/R+x(2)^2)*R/(L-x(1))]; 
    opts=odeset('events',@(t,x) stop_enrolla(t,x,aLimite));
    [~,x]=ode45(f,[0,3],[0,0],opts);
    %coordenadas polares
    r=sqrt((L-x(:,1)).^2+R^2);
    angulo=atan2((L-R*x(:,1)).*sin(x(:,1))-R*cos(x(:,1)),  
(L-R*x(:,1)).*cos(x(:,1))+R*sin(x(:,1)));
    %coordenadas rectangulares
    xp=r.*cos(angulo);
    yp=-r.*sin(angulo);  
    hold on
    %dibuja el cilindro
    z=0:pi/40:2*pi;
    fill(sin(z),cos(z),'g')
    %dibuja la trayectoria de la partícula
    plot(xp,yp)
    hold off
    grid on
    axis equal
    xlabel('x')
    ylabel('y');
    title('Cuerda que se enrolla')
    
    function xb = buscar_intervalos(f,a,b,n)
        x = linspace(a,b,n);
        j = 0; 
        xb=[];
        for i = 1:length(x)-1
            if sign(f(x(i))) ~= sign(f(x(i+1))) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end

    function [value,isterminal,direction]=stop_enrolla(~,x,xFin)
        value=x(1)-xFin; 
        isterminal=1;
        direction=0; 
    end

end

Obtenemos la misma figura

Oscilaciones

Cuando la cuerda no se enrolla completamente y no alcanza la tensión T=0, la partícula de masa m, unida a la cuerda que parte de ángulo φ₀>0, oscila

Se resuelve la ecuación diferencial

${\displaystyle (l_0-R\phi )\frac{d^2\phi }{d{t}^2}=g\cos \phi +R{\left(\frac{d\phi }{dt}\right)}^2}$

con las condiciones iniciales, φ=φ₀, dφ/dt=0.

Se introduce

• La longitud l₀ de la cuerda, en el control titulado Longitud cuerda
• El ángulo inicial φ₀ en grados, en el control titulado Angulo cuerda
• Se ha fijado el radio del cilindro en R=1 m

Se pulsa el botón titulado Nuevo

Se observa una oscilación completa del péndulo

Referencias

Theoretical Question 1. A swing with a Falling Weight. IPHO problems and solutions. 2003 Taiwan

Kirk T. McDonald. A Pendulum Problem. October 2025