El bucle (III)

Movimiento en un bucle (III)

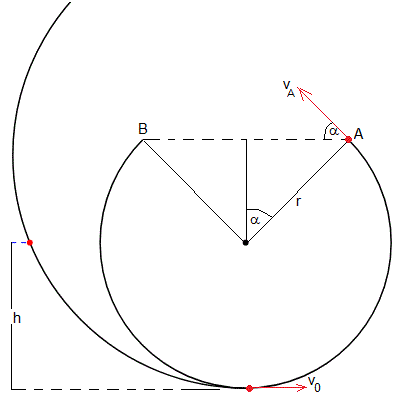
Consideremos un bucle de radio r en el que se ha cortado una sección simétrica de ángulo 2α, tal como se ve en la figura.

Queremos encontrar la altura h, por encima de la parte inferior del bucle, a la que tenemos que dejar caer un objeto, para que perdiendo el contacto en A, vuele en el aire describiendo una trayectoria parabólica y alcance el punto B reingresando en el bucle.

Trayectoria parabólica de A a B

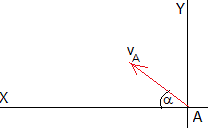
Una partícula que describa el bucle, lo abandona en el punto A, describiendo una trayectoria parabólica con velocidad de tiro v_A y ángulo de disparo α, el ángulo de la tangente a la circunferencia de radio r en A

Para que la partícula impacte en B (y=0) con la misma velocidad v_A (tangente al bucle en B) y continue su movimiento en el bucle, se tiene que cumplir que el alcance sea la distancia de A a B, 2rsinα

Situamos el origen en el punto A, y los ejes como se indica en la figura, las ecuaciones del movimiento de la partícula son:

$\vec{a} {\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} \vec{v} {\begin{cases} v_{x} = v_{A} \cos α \\ v_{y} = v_{A} \sin α - g t \end{cases} \vec{r} {\begin{cases} x = v_{A} \cos α \cdot t \\ y = v_{A} \sin α \cdot t - \frac{1}{2} g t^{2} \end{cases}$

Poniendo y=0, obtenemos el tiempo de vuelo, 2v_Asinα/g, y conocido el alcance x (distancia AB), despejamos la velocidad de disparo v_A

$v_{A}^{2} = \frac{g r}{\cos α}$

Altura crítica

Para que la partícula llegue a A con velocidad v_A, su velocidad v₀ en la parte más baja del bucle deberá ser

$\begin{array}{l} \frac{1}{2} m v_{0}^{2} = m g r + m g r \cos α + \frac{1}{2} m v_{A}^{2} \\ v_{0}^{2} = 2 g (1 + \cos α) r + \frac{g r}{\cos α} \end{array}$

La partícula puede llegar a la base del bucle con velocidad v₀, deslizando sin rozamiento a lo largo de un plano inclinado o cualquier otra trayectoria descendente, la altura h a la que se tiene que soltar es

$m g h = \frac{1}{2} m v_{0}^{2}$

La relación entre la altura h y el ángulo α de la apertura es

$\frac{h}{r} = 1 + \cos α + \frac{1}{2 \cos α}$

Representamos en el eje horizontal el ángulo α, y en el eje vertical h/r

f=@(x) 1+cos(x)+1./(2*cos(x));
fplot(f,[0*pi/180,70*pi/180])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3', '5\pi/12', 
'\pi/2'})
grid on
xlabel('\alpha')
ylabel('h/r')
title('tiro parabólico')

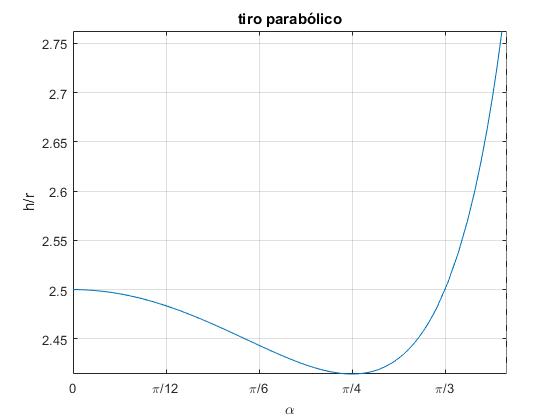
Observamos que la función tiene un mínimo en α=π/4 (45°). Hállese la derivada primera de la función e iguálese a cero. Por lo que

$\frac{h}{r} \geq \sqrt{2} + 1$

Actividades

Se introduce

La altura h a la que se deja caer la partícula, en el control titulado Altura. El máximo valor es 2.8 m
El ángulo de corte α, en el control titulado Angulo de corte. El máximo valor es 70°
El radio r del bucle se ha fijado en 1 m

Observamos como la partícula baja deslizando por una pista circular de radio 1.6·r y entra en el bucle. Pueden ocurrir los siguientes casos:

Que la partícula no tenga suficiente velocidad v₀ en la base del bucle para alcanzar el punto más alto y describir la trayectoria circular. Esta situación se ha descrito en detalle en la página titulada El bucle (II)
Que la partícula describa la trayectoria parabólica que parte de A y llega al punto simétrico B ingresando de nuevo en el bucle y repitiendo indefinidamente el movimiento. Denominaremos h_c a la altura de partida en esta situación
Si la altura de partida h>h_c, la partícula describe una trayectoria parabólica que parte de A y se detiene al llegar al eje Y
Si la altura de partida h<h_c, la partícula describe una trayectoria parabólica que parte de A y se detiene al chocar con el bucle

Ejemplo

El ángulo de corte α=45°. La altura crítica

$h_{c} = 1 (1 + \cos 45 º + \frac{1}{2 \cos 45 º}) = 2.41 m$

Introducimos este valor en el control Altura, observamos la trayectoria parabólica en la parte superior del bucle en el que se ha hecho el corte, a continuación, prosigue su recorrido en el bucle, llega a la posición más baja y repite el movimiento

Altura:
Angulo de corte

Referencias

A. A. Pinsky. Problems in Physics. Problem 12.9 (37), solution (167-168), Mir Publishers 1980