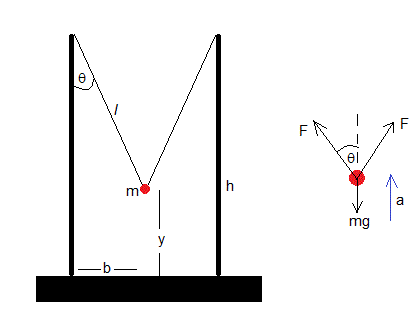
Sean dos postes iguales de altura h, separados una distancia 2b. Una partícula de masa m está unida mediante dos gomas elásticas iguales de constante k a los extremos de los postes.

La partícula se suelta en el suelo y=0, y se desplaza verticalmente, en el instante t su altura es y, tal como se aprecia en la figura.

A la derecha se dibujan las fuerzas sobre la partícula. La fuerza F que ejerce cada una de las gomas estiradas y el peso. Para que la partícula ascienda se tiene que cumplir que en la posición inicial y=0, 2Fcosθ>mg

La longitud l de cada goma estirada es

${\displaystyle l=\frac{b}{\sin \theta }=\sqrt{{\left(h-y\right)}^2+b^2}}$

con cosθ=(h-y)/l

Como en los muelles, la fuerza que ejerce cada goma es proporcional a la deformación, F=k(l-l₀), siendo l₀ la longitud de la goma sin deformar. Haciendo que b>l₀ nos aseguramos que las gomas se encuentran estiradas en cualquier posición y de la partícula

La ecuación del movimiento

Conocidas las fuerzas sobre la partícula, la ecuación del movimiento es

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}=2F\cos \theta -mg\\ \frac{d^{2}y}{d{t}^2}={\omega }^2\left(1-\frac{l_0}{\sqrt{{\left(h-y\right)}^2+b^2}}\right)\left(h-y\right)-g{\omega }^2=2\frac{k}{m}\end{array}}$

Para que se inicie el movimiento de la partícula en y=0, partiendo del reposo, la aceleración tiene que ser positiva, es decir

${\displaystyle {\omega }^2\left(1-\frac{l_0}{\sqrt{h^2+b^2}}\right)h>g}$

Integraremos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, y=0 y dy/dt=0. La partícula fijada al suelo, se suelta en el instante inicial

w2=3.2; %cuadrado de la frecuencia angular 2k/m
h=29; %altura
l0=10; %longitud inicial
b=10.1; %mitad de la separación

f=@(t,x) [x(2);w2*(1-l0/sqrt((h-x(1))^2+b^2))*(h-x(1))-9.8]; 
[t,x]=ode45(f,[0,5],[0,0]);

subplot(2,1,1)
plot(t,x(:,1))
line([0,5],[h,h],'lineStyle','--','color','k')
grid on
xlabel('t')
ylabel('y');
title('Posición')

subplot(2,1,2)
plot(t,x(:,2))
grid on
xlabel('t')
ylabel('v');
title('Velocidad')

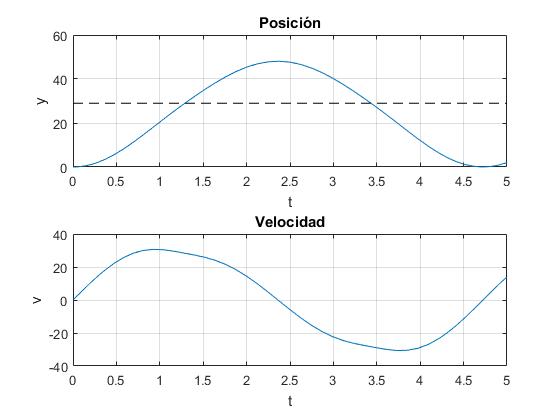
La línea a trazos en la primera figura (posición) señala la altura h de los postes

Vemos que la partícula alcanza su altura máxima cuando su velocidad es cero. La partícula alcanza una velocidad máxima cuando su aceleración es cero. Estas situaciones las estudiaremos en el siguiente apartado

Conservación de la energía

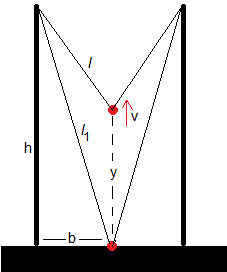
En la situación inicial, las gomas tienen una longitud l₁, la partícula está en reposo en el origen. La energía inicial es la potencial elástica debida a la deformación de las gomas

${\displaystyle E=2\left(\frac{1}{2}k{\left(l_1-l_0\right)}^2\right)=k{\left(\sqrt{h^2+b^2}-l_0\right)}^2}$

Cuando la partícula se encuentra a una altura y, la energía E se reparte en cinética, potencial gravitatoria y potencial elástica

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}^2+mgy+2\left(\frac{1}{2}k{\left(l-l_0\right)}^2\right)\\ E=\frac{1}{2}m{v}^2+mgy+k{\left(\sqrt{{\left(h-y\right)}^2+b^2}-l_0\right)}^2\end{array}}$

El principio de conservación de la energía se escribe

${\displaystyle v^2={\omega }^2\left\{{\left(\sqrt{h^2+b^2}-l_0\right)}^2-{\left(\sqrt{{\left(h-y\right)}^2+b^2}-l_0\right)}^2\right\}-2gy}$

• La máxima velocidad v se alcanza cuando la aceleración es nula.

Resolvemos la ecuación trascendente, para calcular la altura y₀ para la cual la aceleración es nula

${\displaystyle {\omega }^2\left(1-\frac{l_0}{\sqrt{{\left(h-y\right)}^2+b^2}}\right)\left(h-y\right)-g=0}$

La velocidad para esta altura y₀ se calcula aplicando el principio de conservación de la energía

${\displaystyle v^2={\omega }^2\left\{{\left(\sqrt{h^2+b^2}-l_0\right)}^2-{\left(\sqrt{{\left(h-y_0\right)}^2+b^2}-l_0\right)}^2\right\}-2g{y}_0}$

w2=3.2; %cuadrado de la frecuencia angular 2k/m
h=29; %altura
l0=10; %longitud inicial
b=10.1; %mitad de la separación

f=@(y) w2*(1-l0/sqrt((h-y)^2+b^2))*(h-y)-9.8; 
y0=fzero(f,[0,h]);
v0=sqrt(w2*(sqrt(h^2+b^2)-l0)^2-(sqrt((h-y0)^2+b^2)-l0)^2-2*9.8*y0);
disp([y0,v0])

   18.8485   31.3719

La altura y₀=18.8 m, para la cual la velocidad de la partícula v₀=31.4 m/s es máxima

• Calculamos la velocidad de la partícula cuando su altura es y=h

El principio de conservación de la energía se escribe

${\displaystyle v^2={\omega }^2\left(h^2-2l_0\sqrt{h^2+b^2}+2b{l}_0\right)-2gh}$

w2=3.2; %cuadrado de la frecuencia angular 2k/m
h=29; %altura
l0=10; %longitud inicial
b=10.1; %mitad de la separación
 
v=sqrt(w2*(h^2-2*l0*sqrt(h^2+b^2)+2*b*l0)-2*9.8*h);
disp([h,v])

   29.0000   28.3524

La partícula alcanza la velocidad v=28.3 m/s a la altura y=29 m de los postes

• La partícula alcanza su altura máxima cuando su velocidad v=0.

El principio de conservación de la energía se escribe

${\displaystyle {\omega }^2\left\{{\left(\sqrt{h^2+b^2}-l_0\right)}^2-{\left(\sqrt{{\left(h-y\right)}^2+b^2}-l_0\right)}^2\right\}-2gy=0}$

Para calcular la altura y_m resolvemos la ecuación trascendente

w2=3.2;
h=29; %altura
l0=10; %longitud inicial
b=10.1; %mitad de la separación

f=@(y) w2*((sqrt(h^2+b^2)-l0)^2-(sqrt((h-y)^2+b^2)-l0)^2)-2*9.8*y;
ym=fzero(f,[h,2*h]);
disp([ym,0])

48.0823         0

La altura máxima y_m=48.1 m

Actividades

Se introduce

• El cuadrado de la frecuencia angular ω²=2k/m, en el control titulado Cuadrado frec. angular

Se ha fijado

• la altura h=29 m de los postes
• la distancia 2b entre los postes, b=10.1 m
• la longitud de la gomas sin deformar l₀=10 m

Se pulsa el botón titulado Nuevo

Observamos el movimiento vertical de la partícula, las fguerzas que actúan sobre la misma. Un diagrama en forma de tarta muestra como se distribuye para cada posición la energía inicial en:

• energía potencial elástica de las gomas estiradas
• energía potencial gravitatoria
• energía cinética

Se proporcionan los datos del tiempo t, la altura y y la velocidad v=dy/dt

Referencias

Theron W F D. The dynamics of a bungee rocket. Eur. J. Phys. 23 (2002), pp. 643-650