Un bloque desliza a lo largo de un plano inclinado y deforma un muelle (I)
Estudio energético del sistema
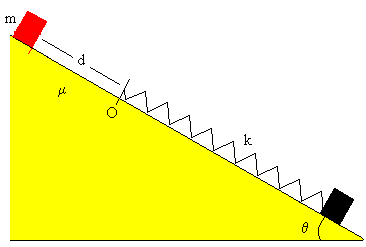
Un bloque de masa m desliza a lo largo de un plano inclinado de ángulo θ. Parte del reposo a una distancia d del muelle elástico sin deformar de constante k. Calcular la máxima deformación del muelle. Se supone que el plano no es liso, sino que ejerce una fuerza de rozamiento de coeficiente μk sobre el bloque que desliza a lo largo del mismo.
Comparamos la situación inicial y la situación final
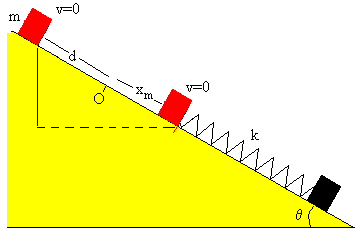
Situamos el nivel cero de energía potencial en el origen O. El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía inicial y la energía final
Por ejemplo, si d=1.0 m, θ=30º, μk=0.3, k=50 N/m, m=1.0 kg
Resolvemos la ecuación de segundo grado en xm y tomamos la raíz positiva xm=0.357 m=35.7 cm
El problema, como vamos a ver a lo largo de esta página, es susceptible de un estudio más detallado
El bloque desliza por el plano inclinado hacia abajo
Se sitúa el bloque parte de la posición x0 con velocidad inicial nula. Supondremos que el bloque desliza a lo largo del plano inclinado desde la posición x0<0 hasta el origen
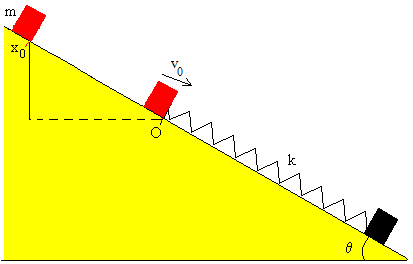
La fuerza de rozamiento vale, fr=μk·N=μk mg·cosθ y se opone al movimiento
El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía final e inicial. Situamos el nivel cero de energía potencial en el origen. La velocidad v0 con la que el cuerpo llega al origen x=0, es
El bloque en contacto con el muelle, desliza hacia abajo.
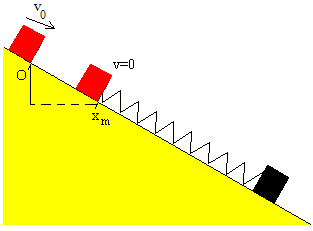
El balance energético cuando el cuerpo se mueve desde el origen a la posición x>0 se escribe
El bloque se detiene en la posición xm en el instante en el que la velocidad v=0. Calculamos la raíz positiva de la ecuación de segundo grado
El bloque en contacto con el muelle, desliza hacia arriba
El bloque parte de xm con velocidad inicial nula siempre que se cumpla que
kxm-mgsinθ ≥ μsmgcosθ,
ω2xm≥a-
en caso contrario la posición xm será la posición final del bloque en reposo. Supongamos que se cumple la primera condición.
El balance energético cuando el cuerpo se mueve desde la posición xm hacia el origen se escribe
- Pasa por el origen
- Se para antes de llegar al origen
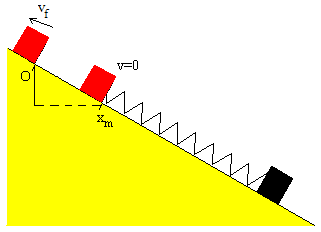
Calculamos la velocidad vf del bloque cuando llega al origen x=0,
A continuación, el bloque deja de tener contacto con el muelle y desliza por el plano inclinado hacia arriba, como describiremos más adelante.
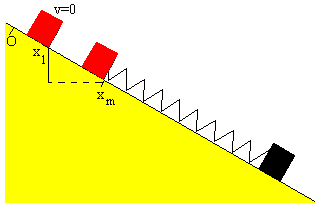
La energía cinética no puede ser negativa, en el caso de que el radicando sea negativo, el bloque se para antes de llegar al origen en la posición x1 en la que v=0
A continuación, el bloque en reposo se detiene definitivamente, o empieza a deslizar hacia abajo, como veremos más adelante.
El bloque desliza hacia arriba
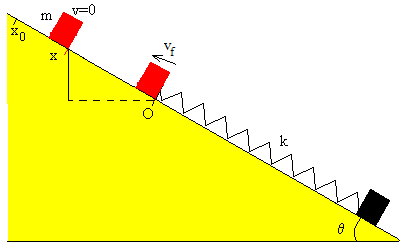
Si el bloque no está sujeto al muelle, el bloque continuará moviéndose hacia arriba hasta que su velocidad sea cero
El bloque en contacto con el muelle, desliza hacia abajo
Volverá a deslizar a lo largo del plano inclinado, hacia abajo, si
mgsinθ-kx1≥μk·mgcosθ,
ω2x1≤a+
Si se cumple esta condición el máximo desplazamiento de móvil x2>x1 se calcula aplicando el balance energético
y así, sucesivamente.
Ejemplo
- Coeficiente de rozamiento μs=μk=0.3
- Masa del bloque, m=1 kg
- Angulo del plano inclinado θ=30º
- Constante elástica del muelle, k=50 N/m
- Posición inicial del bloque x=-1.0 m
El bloque desliza por el plano inclinado, hacia abajo
Como tanθ≥μ, tan30≥0.3, el bloque desliza hacia abajo
La aceleración del bloque es
a+=g(sinθ-μcosθ)=9.8·(sin30º-0.3·cos30º)=2.35 m/s
El tiempo t que tarda en llegar al origen x=0
0=-1.0+a+t2/2, t=0.92 s
La velocidad v del bloque
v=a+t, v0=2.17 m/s
Balance energético
La fuerza de rozamiento vale fr= μmgcosθ=0.3·1.0·9.8·cos30=2.55 N
El bloque en contacto con el muelle, desliza hacia abajo
La frecuencia angular ω2=k/m=50
El tiempo que tarda en alcanzar el máximo desplazamiento, v=0, es
El máximo desplazamiento xm es
Balance energético
Se resuelve la ecuación de segundo grado para calcular xm=0.357 m
El bloque, en contacto con el muelle, desliza hacia arriba
La aceleración
a-=g(sinθ+μcosθ)=9.8·(sin30º+0.3·cos30º)=7.45 m/s
El bloque vuelve a pasar por el origen y tarda un tiempo
La velocidad vf del bloque cuando pasa por el origen es
Balance energético
El bloque desliza hacia arriba
v=-1.03 +7.45 t
x=-1.03·t +7.45·t2/2
La velocidad v se hace cero, en el instante t=0.14 s, x0=-0.072 m
El bloque completa un ciclo, y retorna hacia el origen, deslizando por el plano inclinado
x=-0.072+a+t2/2,
v=a+t,
cuando pasa por el origen x=0, t=0.24 s, v0=0.58 m/s
El bloque en contacto con el muelle, desliza hacia abajo
El tiempo que tarda en alcanzar el máximo desplazamiento es
El máximo desplazamiento xm es
En esta posición
kxm-mgsinθ ≤ μsmgcosθ,
1.19<2.55
El bloque permanece definitivamente en reposo en esta posición
Actividades
Se introduce
- El coeficiente de rozamiento μs=μk, entre el bloque y el plano sobre el cual desliza, en el control titulado Coef. rozamiento.
- El ángulo del vértice del plano inclinado en grados, en el control titulado Ángulo.
- La constante k del muelle elástico en N/m, en el control titulado Cte. muelle.
- La masa m del bloque en kg, ese ha fijado en m=1 kg.
- La posición inicial del bloque se ha fijado en x0=-1.0 m.
Se pulsa el botón titulado Nuevo.
Se proporcionan los datos relativos, al tiempo, t, en segundos, la posición x en cm y la velocidad v del bloque en m/s, y la energía del sistema formado el bloque y el muelle, en cada instante.
Se dibujan mediante fechas las fuerzas sobre el bloque:
- Componente del peso a lo largo del plano inclinado
- Fuerza de rozamiento
- Fuerza que ejerce el muelle deformado
En la parte superior derecha, muestra en un diagrama de barras la energía del sistema en cada instante.
- El rectángulo de color negro, es la energía inicial
- En color rojo, la energía potencial elástica del muelle deformado, que es siempre positiva
- En color azul, la energía cinética del bloque
- El color rosa, la energía potencial, que puede ser positiva o negativa, dependiendo de que el cuerpo esté por encima o por debajo del origen.
La energía va disminuyendo debido al trabajo de la fuerza de rozamiento.

