A. R. Marlow describe una sorprendente demostración mecánica en un artículo publicado en American Journal of Physics en el año 1991 originalmente publicada en 1926 en una revista para magos.
Los materiales necesarios son muy simples: una caja de cerillas, un manojo de llaves, un trozo de cuerda y un lápiz. Con una mano se sujeta el lápiz y se le rodea con la cuerda de modo que las llaves cuelgan de un extremo. Con la otra mano se sujeta la caja de cerillas unida al otro extremo de la cuerda, la cuerda se mantiene tensa horizontal un poco por debajo del nivel del lápiz. Después suelta, y aquí viene la sorpresa, el manojo de llaves mucho más pasado que la caja de cerillas se detiene mientras la cuerda da vueltas alrededor del lápiz que se mantiene fijo.

Una demostración espectacular por lo grandiosa, fué emitida en horario de máxima audiencia en el programa el Hormiguero de Antena 3 TV. En YouTube se pueden encontrar varios vídeos

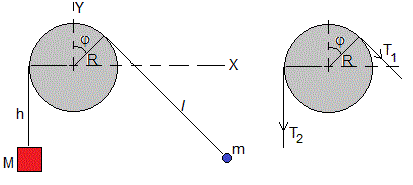
Vamos a estudiar el sistema formado por una partícula de masa m y un cuerpo que cuelga de masa M mucho mayor. Ambos están unidos por una cuerda inextensible y de masa despreciable de longitud l₀ que pasa por una varilla horizontal de forma cilíndrica de radio R, bien sujeta.

La cuerda puede deslizar sobre la varilla, la fuerza de rozamiento, que depende del ángulo de contacto, π/2+φ, hace que las tensiones de la cuerda a ambos lados de la varilla sean diferentes tal como se ha explicado en la página titulada Rozamiento de la cuerda sobre una polea. Cuando desliza

${\displaystyle T_2=T_1\exp \left({\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)}$

Posición, velocidad y aceleración de la partícula

Sea $l=l_0-R\left(\frac{\pi }{2}+\phi \right)-h$, la longitud de la porción de cuerda que une la partícula y la varilla y que es tangente a la misma

La posición de la partícula en el Sistema de Referencia de la figura es

${\displaystyle \{\begin{array}{l}x=R\sin \phi +l\cos \phi \\ y=R\cos \phi -l\sin \phi \end{array}}$

Derivamos con respecto del tiempo para obtener las componentes de la velocidad

${\displaystyle \{\begin{array}{l}\frac{dx}{dt}=\left(R\cos \phi -l\sin \phi \right)\frac{d\phi }{dt}+\cos \phi \frac{dl}{dt}\\ \frac{dy}{dt}=\left(-R\sin \phi -l\cos \phi \right)\frac{d\phi }{dt}-\sin \phi \frac{dl}{dt}\end{array}}$

Derivamos respecto del tiempo para obtener las componentes de la aceleración

${\displaystyle \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\left(R\cos \phi -l\sin \phi \right)\frac{d^2\phi }{d{t}^2}+\cos \phi \frac{d^{2}l}{d{t}^2}+\left(-R\sin \phi -l\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\sin \phi \frac{d\phi }{dt}\frac{dl}{dt}\\ \frac{d^{2}y}{d{t}^2}=\left(-R\sin \phi -l\cos \phi \right)\frac{d^2\phi }{d{t}^2}-\sin \phi \frac{d^{2}l}{d{t}^2}+\left(-R\cos \phi +l\sin \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\cos \phi \frac{d\phi }{dt}\frac{dl}{dt}\end{array}}$

La posición del cuerpo de masa M es -h

Ecuaciones del movimiento

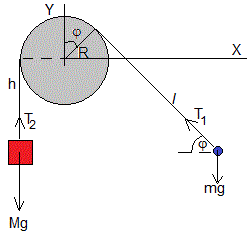
El movimiento de este sistema tiene dos o más etapas etapas:

• El cuerpo de masa M, parte del reposo a la altura del eje de la varilla, se desplaza una altura h hasta que vuelve a detenerse

• El cuerpo permanece en reposo y la partícula continua dando vueltas alrededor de la varilla. Una situación similar a la estudiada en la página titulada Movimiento de una partícula atada a una cuerda que se enrolla en un cilindro horizontal (II)

• Cuando la masa del cuerpo M es grande y la masa de la partícula m es pequeña el movimiento consta esencialmente de dos etapas. A medida que la partícula da vueltas alrededor de la varilla, se incrementa la tensión de la cuerda T₁, cuando supera un valor crítico, el cuerpo comienza a ascender

El cuerpo desciende

Las tensiones iniciales de la cuerda son T₂=Mg y T₁=mgsinφ₀. φ₀ es el ángulo que forma la cuerda con la horizontal en la situación inicial t=0.

La cuerda desliza sobre la varilla si $Mg\ge mg·\sin {\phi }_0·\exp \left({\mu }_s\left(\frac{\pi }{2}+{\phi }_0\right)\right)$, μ_s es el coeficiente estático

• Ecuación del movimiento de la partícula

Sobre la partícula de masa m actúan dos fuerzas, la tensión T₁ de la cuerda y el peso mg

${\displaystyle \{\begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-T_1\cos \phi \\ m\frac{d^{2}y}{d{t}^2}=mg-T_1\sin \phi \end{array}}$

• Ecuación del movimiento del cuerpo

Sobre el cuerpo de masa M actúan dos fuerzas, la tensión T₂ de la cuerda y el peso Mg

${\displaystyle M\frac{d^{2}h}{d{t}^2}=Mg-T_2}$

• Relación entre las tensiones T₁ y T₂

Cuando el cuerpo de masa M se desplaza hacia abajo, la cuerda desliza sobre la varilla cilíndrica y la relación entre las tensiones es

${\displaystyle T_2=T_1\exp \left({\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)}$

Donde μ_k es el coeficiente cinético y π/2+φ es el ángulo de contacto entre la cuerda y la superficie cilíndrica de radio R

La tarea consiste en expresar las ecuaciones del movimiento en términos de dos variables l y φ. Resolveremos mediante procedimientros numéricos el sistema de dos ecuaciones diferenciales con las condiciones iniciales especificadas

Expresamos la aceleración del cuerpo de masa M, d²h/dt² en términos de l y φ

${\displaystyle \begin{array}{l}{l}_0=l+R\left(\frac{\pi }{2}+\phi \right)+h\\ \frac{d^{2}h}{d{t}^2}=-R\frac{d^2\phi }{d{t}^2}-\frac{d^{2}l}{d{t}^2}\end{array}}$

Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left(R\cos \phi -l\sin \phi \right)\frac{d^2\phi }{d{t}^2}+\cos \phi \frac{d^{2}l}{d{t}^2}+\left(-R\sin \phi -l\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\sin \phi \frac{d\phi }{dt}\frac{dl}{dt}=-\frac{T_1}{m}\cos \phi \\ \left(-R\sin \phi -l\cos \phi \right)\frac{d^2\phi }{d{t}^2}-\sin \phi \frac{d^{2}l}{d{t}^2}+\left(-R\cos \phi +l\sin \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\cos \phi \frac{d\phi }{dt}\frac{dl}{dt}=\frac{T_1}{m}\sin \phi -g\end{array}\\ -R\frac{d^2\phi }{d{t}^2}-\frac{d^{2}l}{d{t}^2}=g-\frac{T_1}{M}\exp \left({\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)\end{array}}$

Despejamos la tensión T₁ de la última y la sustituimos en las dos primeras, quedando el sistema de dos ecuaciones diferenciales

${\displaystyle \{\begin{array}{l}\left(R\cos \phi -l\sin \phi \right)\frac{d^2\phi }{d{t}^2}+\cos \phi \frac{d^{2}l}{d{t}^2}+\left(-R\sin \phi -l\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\sin \phi \frac{d\phi }{dt}\frac{dl}{dt}=-\frac{M}{m}\left(g+R\frac{d^2\phi }{d{t}^2}+\frac{d^{2}l}{d{t}^2}\right)\exp \left(-{\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)\cos \phi \\ \left(-R\sin \phi -l\cos \phi \right)\frac{d^2\phi }{d{t}^2}-\sin \phi \frac{d^{2}l}{d{t}^2}+\left(-R\cos \phi +l\sin \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\cos \phi \frac{d\phi }{dt}\frac{dl}{dt}=\frac{M}{m}\left(g+R\frac{d^2\phi }{d{t}^2}+\frac{d^{2}l}{d{t}^2}\right)\exp \left(-{\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)\sin \phi -g\end{array}}$

Llamamos

${\displaystyle \xi =\frac{M}{m}\exp \left(-{\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)}$

El sistema se convierte en

${\displaystyle \{\begin{array}{l}\left((\xi +1)R\cos \phi -l\sin \phi \right)\frac{d^2\phi }{d{t}^2}+(\xi +1)\cos \phi \frac{d^{2}l}{d{t}^2}=-\xi g\cos \phi +\left(R\sin \phi +l\cos \phi \right){\left(\frac{d\phi }{dt}\right)}^2+2\sin \phi \frac{d\phi }{dt}\frac{dl}{dt}\\ \left((\xi +1)R\sin \phi +l\cos \phi \right)\frac{d^2\phi }{d{t}^2}+(\xi +1)\sin \phi \frac{d^{2}l}{d{t}^2}=g-\xi g\sin \phi -\left(R\cos \phi -l\sin \phi \right){\left(\frac{d\phi }{dt}\right)}^2-2\cos \phi \frac{d\phi }{dt}\frac{dl}{dt}\end{array}}$

Despejamos las derivadas segundas

${\displaystyle \begin{array}{l}\{\begin{array}{l}{a}_1\frac{d^2\phi }{d{t}^2}+b_1\frac{d^{2}l}{d{t}^2}=c_1\\ a_2\frac{d^2\phi }{d{t}^2}+b_2\frac{d^{2}l}{d{t}^2}=c_2\end{array}\\ \frac{d^2\phi }{d{t}^2}=\frac{\left|\begin{array}{cc}{c}_1& b_1\\ c_2& b_2\end{array}\right|}{\left|\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right|}=\frac{c_1{b}_2-c_2{b}_1}{a_1{b}_2-a_2{b}_1}\\ \frac{d^{2}l}{d{t}^2}=\frac{\left|\begin{array}{cc}{a}_1& c_1\\ a_2& c_2\end{array}\right|}{\left|\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right|}=\frac{a_1{c}_2-a_2{c}_1}{a_1{b}_2-a_2{b}_1}\end{array}}$

Ejemplo

Consideremos el siguiente sistema

• Cociente de las masas, M/m=6.49
• Longitud de la cuerda, l₀=0.44 m
• Radio de la varilla cilíndrica, R=0.0075 m
• Coeficiente cinético, μ_k=0.195

Condiciones iniciales

• Ángulo inicial, φ₀=0.1765 (10.1°), por debajo de la horizontal
• La partícula se suelta, dφ/dt=0
• Altura inicial del cuerpo, h=0
• Longitud inicial l=l₀-R(π/2+φ₀) de la porción de cuerda que une la partícula y el cilindro y que es tangente al mismo
• Si el cuerpo se suelta, dh/dt=0, por lo que dl/dt=0

${\displaystyle \begin{array}{l}{l}_0=l+R\left(\frac{\pi }{2}+\phi \right)+h\\ \frac{dh}{dt}=-R\frac{d\phi }{dt}-\frac{dl}{dt}\end{array}}$

Primero, verificamos que la cuerda desliza sobre la varilla cilíndrica

A continuación, se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB. Se interumpe el procedimiento cuando el cuerpo de masa M vuelve al estado de reposo, dh/dt=0, después de desplazarse una altura h medida desde el centro de la varilla

function looping_2
    M=6.49; %masa 
    th_0=0.1765; %ángulo inicial 
    L0=0.44; %longitud cuerda
    mu=0.195; %coeficiente cinético
    R=0.0075; %radio
    if M<sin(th_0)*exp(mu*(pi/2+th_0)) %verifica si la cuerda desliza
        disp([M,sin(th_0)*exp(mu*(pi/2+th_0))])
        return;
    end

    opts=odeset('events',@stop_cuerda);
    [t,x]=ode45(@cuerda,[0,5],[L0-R*(pi/2+th_0),0,th_0,0], opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    hold on
    plot(X,Y)
    %dibuja el cilindro
    z=0:pi/40:2*pi;
    fill(R*sin(z),R*cos(z),[0.8 0.8 0.8])
    fplot(@(z) R*cos(z), @(z) R*sin(z), [-x(end,3),pi],'lineWidth',
1.5,'color','k')
    h=L0-x(end,1)-R*(x(end,3)+pi/2); %altura del cuerpo
    line([-R,-R],[0,-h], 'lineWidth',1.5,'color','k')
    plot(-R,-h,'ro','markersize',7,'markeredgecolor','r',
'markerfacecolor','r')
    line([R*sin(x(end,3)),X(end)],[R*cos(x(end,3)), Y(end)],
'lineWidth',1.5,'color','k')
    plot(X(end),Y(end),'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
    hold off
    disp([t(end),x(end,1),x(end,2), x(end,3),x(end,4), X(end), Y(end)])
    grid on
    axis equal
    xlabel('x')
    ylabel('y');
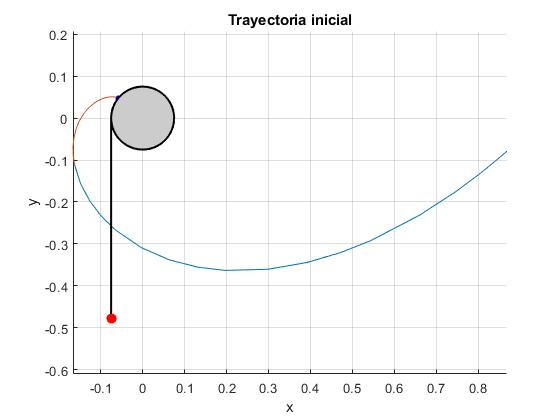
    title('Trayectoria inicial')

% x(1) es l, x(3) es phi
    function dr=cuerda(~, x)
        xi=M*exp(-mu*(x(3)+pi/2));
        a1=(xi+1)*R*cos(x(3))-x(1)*sin(x(3));
        a2=(xi+1)*R*sin(x(3))+x(1)*cos(x(3));
        b1=(xi+1)*cos(x(3));
        b2=(xi+1)*sin(x(3));
        c1=-xi*9.8*cos(x(3))+(R*sin(x(3))+x(1)*cos(x(3)))*x(4)^2+
2*sin(x(3))*x(4)*x(2);
        c2=9.8-xi*9.8*sin(x(3))-(R*cos(x(3))-x(1)*sin(x(3)))*x(4)^2-
2*cos(x(3))*x(4)*x(2);
        den=a1*b2-a2*b1;
        dr=[x(2);(a1*c2-a2*c1)/den;x(4);(c1*b2-c2*b1)/den];
    end
    function [value,isterminal,direction]=stop_cuerda(~,x)
        dh=-R*x(4)-x(2); %velocidad de la masa M
        value=dh;
        isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end

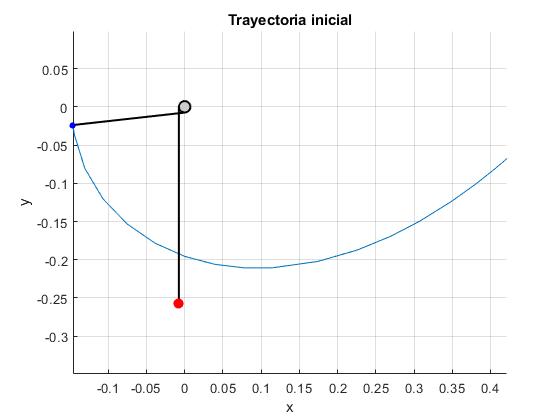
Los resultados son los siguientes:

• Tiempo hasta que el cuerpo se detiene, t₁=0.3183 s
• Longitud de la porción de cuerda que une la partícula y la varilla, l₁=0.1477 m
• Posición angular de la partícula, φ₁=3.0305 (173.6°)
• Con estos dos datos, deducimos la altura del cuerpo, h=l₀-l-R(π/2+φ)=0.2577 m
• Velocidad angular (dφ/dt)₁=28.4082 rad/s
• Posición final de la partícula: x₁=-0.1460 m, y₁=-0.0238 m, punto de color azul al final de la trayectoria, a la izquierda de la figura

El cuerpo en reposo

En la página titulada Movimiento de una partícula atada a una cuerda que se enrolla en un cilindro horizontal (II), hemos estudiado este caso. Reproducimos los resultados más importantes obtenidos en dicha página

• La ecuación diferencial del movimiento de la partícula es

${\displaystyle (l_0-R\phi )\frac{d^2\phi }{d{t}^2}=g\cos \phi +R{\left(\frac{d\phi }{dt}\right)}^2}$

• La energía de la partícula es

${\displaystyle E=\frac{1}{2}m{\left(l_0-R\phi \right)}^2{\left(\frac{d\phi }{dt}\right)}^2+mg\left(R\cos \phi -\left(l_0-R\phi \right)\sin \phi \right)}$

• La tensión de la cuerda es

${\displaystyle \[ \frac{T_1}{m}=g\sin \phi +\left(l_0-R\phi \right){\left(\frac{d\phi }{dt}\right)}^2 \]}$

Donde l₀=l₁+Rφ₁=0.1705 m es la longitud de la cuerda que se considera

Tensión de la cuerda

A medida que se enrolla la cuerda en la varilla, aumenta la velocidad angular dφ/dt, aumenta por tanto, la tensión T₁. Podría llegar un momento en el que se cumpliese que $T_1\ge Mg\exp \left({\mu }_s\left(\frac{\pi }{2}+\phi \right)\right)$, la cuerda empezaría a deslizar sobre la varilla y el cuerpo de masa M se movería hacia arriba.

En la ecuación de la energía despejamos la velocidad angular dφ/dt. E es la energía de la partícula en el instante t₁. Representamos la tensión T₁/m en función del ángulo φ>φ₁ y lo comparamos con la máxima $Mg\exp \left({\mu }_s\left(\frac{\pi }{2}+\phi \right)\right)$

function looping_1
    M=6.49; %masa 
    th_0=0.1765; %ángulo inicial 
    L0=0.44; %longitud cuerda
    mu=0.195; %coeficiente cinético
    R=0.0075; %radio

    opts=odeset('events',@stop_cuerda);
    [~,x]=ode45(@cuerda,[0,5],[L0-R*(pi/2+th_0),0,th_0,0], opts);

    lon=x(end,1)+R*x(end,3);
    E=(lon-R*x(end,3))^2*x(end,4)^2/2+9.8*(R*cos(x(end,3))-
(lon-R*x(end,3))*sin(x(end,3)));
    T=@(z) 9.8*sin(z)+2*(E-9.8*(R*cos(z)-(lon-R*z).*sin(z)))./(lon-R*z);
    hold on
    fplot(T,[x(end,3),x(end,3)+x(end,1)/R]);
    fplot(@(x) M*9.8*exp(mu*(pi/2+x)),[x(end,3),x(end,3)+x(end,1)/R]);
    line([x(end,3)+x(end,1)/R,x(end,3)+x(end,1)/R],[0,7500],'color','k',
'lineStyle','--')
    ylim([0,7500])
    hold off
    grid on
    legend('T_1','T_{máx}','Location','best')
    xlabel('x')
    ylabel('T_1/m');
    title('Tensión')

% x(1) es l, x(3) es phi
    function dr=cuerda(~, x)
        xi=M*exp(-mu*(x(3)+pi/2));
        a1=(xi+1)*R*cos(x(3))-x(1)*sin(x(3));
        a2=(xi+1)*R*sin(x(3))+x(1)*cos(x(3));
        b1=(xi+1)*cos(x(3));
        b2=(xi+1)*sin(x(3));
        c1=-xi*9.8*cos(x(3))+(R*sin(x(3))+x(1)*cos(x(3)))*x(4)^2+
2*sin(x(3))*x(4)*x(2);
        c2=9.8-xi*9.8*sin(x(3))-(R*cos(x(3))-x(1)*sin(x(3)))*x(4)^2-
2*cos(x(3))*x(4)*x(2);    
        den=a1*b2-a2*b1;
        dr=[x(2);(a1*c2-a2*c1)/den;x(4);(c1*b2-c2*b1)/den];
    end
    function [value,isterminal,direction]=stop_cuerda(t,x)
   %x(1) es  x, x(3) es y
        dh=-R*x(4)-x(2); %velocidad de la masa M
        value=dh;
        isterminal=1;    
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end

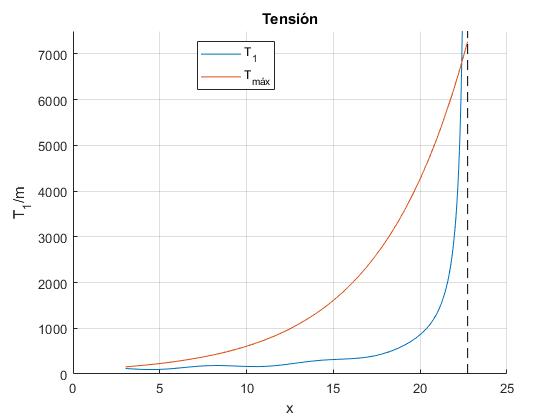
Como apreciamos en la gráfica, T₁≥T_máx, la cuerda empieza a deslizar, o el cuerpo empieza a moverse hacia arriba, un poquito antes de que se encuentre completamente enrollada en la varilla, posición angular de la línea a trazos

Movimiento de la partícula con el cuerpo en reposo

Representamos la trayectoria completa de la partícula resolviendo la ecuación diferencial del movimiento (cuerpo en reposo), con las siguientes condiciones iniciales:

• En el instante t₁
• La posición angular inicial φ₁
• La velocidad angular inicial (dφ/dt)₁

Se detiene el procedimiento cuando la cuerda se ha enrollado completamente en la varilla

function looping
    M=6.49; %masa 
    th_0=0.1765; %ángulo inicial 
    L0=0.44; %longitud cuerda
    mu=0.195; %coeficiente cinético
    R=0.0075; %radio
%primera etapa
    opts=odeset('events',@stop_cuerda);
    [t,x]=ode45(@cuerda,[0,5],[L0-R*(pi/2+th_0),0,th_0,0], opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    hold on
    plot(X,Y)

%segunda etapa
    lon=x(end,1)+R*x(end,3); %longitud inicial
    E0=(lon-R*x(end,3))^2*x(end,4)^2/2+9.8*(R*cos(x(end,3))-
(lon-R*x(end,3))*sin(x(end,3)));
    x0=[x(end,3),x(end,4)]; %condiciones iniciales
    tIni=t(end); %tiempo inicial
    f=@(t,x) [x(2); (9.8*cos(x(1))+R*x(2)^2)/(lon-R*x(1))]; 
    opts=odeset('events',@stop_cuerda_1);
    [~,x]=ode45(f,[tIni,2],x0, opts);
    X=R*sin(x(:,1))+(lon-R*x(:,1)).*cos(x(:,1));
    Y=R*cos(x(:,1))-(lon-R*x(:,1)).*sin(x(:,1));
    plot(X,Y)
    E=(lon-R*x(:,1)).^2.*x(:,2).^2/2+9.8*(R*cos(x(:,1))-
(lon-R*x(:,1)).*sin(x(:,1))); %energía
     z=0:pi/40:2*pi;
    fill(R*sin(z),R*cos(z),[0.8 0.8 0.8])
    plot(X(end),Y(end),'bo','markersize',4,'markeredgecolor','b',
'markerfacecolor','b')
    hold off
    grid on
    axis equal
    xlabel('x')
    ylabel('y');
    title('Trayectoria')

% x(1) es l, x(3) es phi
    function dr=cuerda(~, x)
        xi=M*exp(-mu*(x(3)+pi/2));
        a1=(xi+1)*R*cos(x(3))-x(1)*sin(x(3));
        a2=(xi+1)*R*sin(x(3))+x(1)*cos(x(3));
        b1=(xi+1)*cos(x(3));
        b2=(xi+1)*sin(x(3));
        c1=-xi*9.8*cos(x(3))+(R*sin(x(3))+x(1)*cos(x(3)))*x(4)^2+
2*sin(x(3))*x(4)*x(2);
        c2=9.8-xi*9.8*sin(x(3))-(R*cos(x(3))-x(1)*sin(x(3)))*x(4)^2-
2*cos(x(3))*x(4)*x(2);  
        den=a1*b2-a2*b1;
        dr=[x(2);(a1*c2-a2*c1)/den;x(4);(c1*b2-c2*b1)/den];
    end
    function [value,isterminal,direction]=stop_cuerda(t,x)
   %x(1) es  x, x(3) es y
        dh=-R*x(4)-x(2); %velocidad de la masa M
        value=dh;
        isterminal=1;    
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
    function [value,isterminal,direction]=stop_cuerda_1(t,x)
   %x(1) es  x, x(3) es y
        X=R*sin(x(1))+(lon-R*x(1)).*cos(x(1));
        Y=R*cos(x(1))-(lon-R*x(1)).*sin(x(1));
        value=sqrt(X^2+Y^2)-R; %choca con la varilla
        isterminal=1;    
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end

Comprobamos el principio de conservación de la energía en la segunda etapa del movimiento

    8.5745   %inicial
    ...
    8.5537
    8.5503
    8.5528

El procedimiento ode45 avisa de algunos fallos, que no se producen cuando se emplea el procedimiento Runge-Kutta en la simulación más abajo

Warning: Failure at t=6.738177e-01.  Unable to meet integration tolerances 
without reducing the step size below the smallest value allowed (1.776357e-15) 
at time t.

Aquí se completa la descripción de la demostración mecánica sorpendente, sin embargo, este sistema admite otras posiblidades, dependiendo de la relación de masas M/m, el radio R de la varilla o el coeficiente estático μ_s y cinético μ_k y la longitud de la cuerda l₀

El cuerpo asciende

Si se cumple que $T_1\ge Mg\exp \left({\mu }_s\left(\frac{\pi }{2}+\phi \right)\right)$, el cuerpo empieza a desplazarse hacia arriba, hasta que se detiene.

Cuando la cuerda desliza sobre la varilla la relación entre las tensiones es

${\displaystyle T_1=T_2\exp \left({\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)}$

El único efecto en el sistema de dos ecuaciones diferenciales que describe el movimiento de la partícula es el cambio en el parámetro ξ del término μ_k por -μ_k

${\displaystyle \xi =\frac{M}{m}\exp \left({\mu }_k\left(\frac{\pi }{2}+\phi \right)\right)}$

Se resuelve el sistema de dos ecuaciones diferenciales por procedimientos numéricos con las siguientes condiciones iniciales

• En el instante t₂
• La posición angular de la partícula es φ₂
• La velocidad angular de la partícula es (dφ/dt)₂
• La longitud de la cuerda que une la varilla con la partícula es l=l₀-R(π/2+φ₂)-h
• La velocidad (dl/dt)₂=-R(dφ/dt)₂

Se detiene el procedimiento cuando la velocidad del cuerpo es nula dh/dt=-dl/dt-Rdφ/dt=0

Ejemplo

Consideremos el siguiente sistema

• Cociente de las masas, M/m=6.49
• Longitud de la cuerda, l₀=1 m
• Radio de la varilla cilíndrica, R=0.075 m
• Coeficiente cinético, μ_k=0.195

Vamos a describir las etapas del movimiento del cuerpo de masa M y de la partícula de masa m

• Primera etapa del movimiento, el cuerpo desciende

Primero, verificamos que la cuerda desliza sobre la varilla cilíndrica

    M=6.49; %masa 
    th_0=0.1765; %ángulo inicial 
    L0=1; %longitud cuerda
    mu=0.195; %coeficiente cinético
    R=0.075; %radio

    if M<sin(th_0)*exp(mu*(pi/2+th_0))
        disp([M,sin(th_0)*exp(mu*(pi/2+th_0))])
        return;
    end
...

196.9959  152.9038

A continuación, se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB, se interumpe el procedimiento cuando el cuerpo de masa M vuelve al estado de reposo, dh/dt=0, después de desplazarse una altura h medida desde el centro de la varilla

Condiciones iniciales

• Ángulo inicial, φ₀=0.1765 (10.1°), por debajo de la horizontal
• La partícula se suelta, dφ/dt=0
• Altura inicial del cuerpo, h=0
• Longitud inicial l=l₀-R(π/2+φ₀) de la porción de cuerda que une la partícula y el cilindro y que es tangente al mismo
• Si el cuerpo se suelta, dh/dt=0, por lo que dl/dt=0

...
    opts=odeset('events',@stop_cuerda);
    [~,x]=ode45(@cuerda,[0,2],[L0-R*(pi/2+th_0),0,th_0,0],opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    hold on
    plot(X,Y)
...

Los resultados son los siguientes:

• Tiempo hasta que el cuerpo se detiene, t₁=0.4189 s
• Longitud de la porción de cuerda que une la partícula y la varilla, l₁=0.1821 m
• Posición angular de la partícula, φ₁=2.9275 (167.7°)
• Con estos dos datos, deducimos la altura del cuerpo, h=l₀-l-R(π/2+φ)=0.4805 m
• Velocidad angular (dφ/dt)₁=32.7127 rad/s
• Posición final de la partícula: x₁=-0.1620 m, y₁=-0.1120 m

• Segunda etapa del movimiento

Calculamos la tensión T₁ de la porción de cuerda de longitud l₀=l₁+Rφ₁, cuando el cuerpo está en reposo, entonces la tensión T₂=Mg

...
    lon=x(end,1)+R*x(end,3);
    T1=9.8*sin(x(end,3))+(lon-R*x(end,3))*x(end,4)^2;
    disp([T1,M*9.8*exp(mu*(pi/2+x(end,3)))])
...

196.9959  152.9038

Como apreciamos T₁ es mayor que la $Mg\exp \left({\mu }_s\left(\frac{\pi }{2}+{\phi }_1\right)\right)$, la cuerda desliza y el cuerpo asciende

A continuación, se resuelve el sistema de dos ecuaciones diferenciales por el procedimiento ode45 de MATLAB con el único cambio de sustituir μ_k por -μ_k. Se interumpe el procedimiento cuando el cuerpo de masa M vuelve al estado de reposo, dh/dt=0, o la cuerda se enrolla completamente en la varilla l=R que es lo que ocurre en este caso

Las condiciones iniciales son las finales del sistema anterior

...
    mu=-mu;
    opts=odeset('events',@stop_cuerda_1);
    [t,x]=ode45(@cuerda,[0,5],[x(end,1),x(end,2),x(end,3),x(end,4)], opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    plot(X,Y)
...

Unimos las porciones de código, para dibujar la trayectoria de la partícula

function looping_4
    M=6.49; %masa 
    th_0=0.1765; %ángulo inicial 
    L0=1; %longitud cuerda
    mu=0.195; %coeficiente cinético
    R=0.075; %radio

    if M<sin(th_0)*exp(mu*(pi/2+th_0))
        disp([M,sin(th_0)*exp(mu*(pi/2+th_0))])
        return;
    end
    
    opts=odeset('events',@stop_cuerda);
    [t,x]=ode45(@cuerda,[0,2],[L0-R*(pi/2+th_0),0,th_0,0],opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    hold on
    plot(X,Y)

    lon=x(end,1)+R*x(end,3);
    T1=9.8*sin(x(end,3))+(lon-R*x(end,3))*x(end,4)^2;
    %disp([T1,M*9.8*exp(mu*(pi/2+x(end,3)))])
    
    tIni=t(end);
    mu=-mu;
    opts=odeset('events',@stop_cuerda_1);
    [t,x]=ode45(@cuerda,[tIni,5],[x(end,1),x(end,2),x(end,3),x(end,4)], opts);
    X=R*sin(x(:,3))+x(:,1).*cos(x(:,3));
    Y=R*cos(x(:,3))-x(:,1).*sin(x(:,3));
    plot(X,Y)
    
    plot(X(end),Y(end),'bo','markersize',4,'markeredgecolor',
'b','markerfacecolor','b')
    z=0:pi/40:2*pi;
    fill(R*sin(z),R*cos(z),[0.8 0.8 0.8])
    fplot(@(z) R*cos(z), @(z) R*sin(z), [-x(end,3),pi],
'lineWidth',1.5,'color','k')
    h=L0-x(end,1)-R*(x(end,3)+pi/2);
    line([-R,-R],[0,-h], 'lineWidth',1.5,'color','k')
    plot(-R,-h,'ro','markersize',7,'markeredgecolor','r',
'markerfacecolor','r')
    line([R*sin(x(end,3)),X(end)],[R*cos(x(end,3)), Y(end)],
'lineWidth',1.5,'color','k')
    hold off
    grid on
    axis equal
    xlabel('x')
    ylabel('y');
    title('Trayectoria inicial')

% x(1) es l, x(3) es phi
    function dr=cuerda(~, x)
        xi=M*exp(-mu*(x(3)+pi/2));
        a1=(xi+1)*R*cos(x(3))-x(1)*sin(x(3));
        a2=(xi+1)*R*sin(x(3))+x(1)*cos(x(3));
        b1=(xi+1)*cos(x(3));
        b2=(xi+1)*sin(x(3));
        c1=-xi*9.8*cos(x(3))+(R*sin(x(3))+x(1)*cos(x(3)))*x(4)^2+
2*sin(x(3))*x(4)*x(2);
        c2=9.8-xi*9.8*sin(x(3))-(R*cos(x(3))-x(1)*sin(x(3)))*x(4)^2-
2*cos(x(3))*x(4)*x(2);    
        den=a1*b2-a2*b1;
        dr=[x(2);(a1*c2-a2*c1)/den;x(4);(c1*b2-c2*b1)/den];
    end
    function [value,isterminal,direction]=stop_cuerda(~,x)
   %x(1) es  x, x(3) es y
        dh=-R*x(4)-x(2); %velocidad de la masa M
        value=dh;
        isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
    function [value,isterminal,direction]=stop_cuerda_1(~,x)
   %x(1) es  x, x(3) es y
        X=R*sin(x(3))+x(1).*cos(x(3));
        Y=R*cos(x(3))-x(1).*sin(x(3));
        value=sqrt(X^2+Y^2)-R;
        isterminal=1; %1 detiene la integración cuando la velocidad se hace cero   
        direction=-1; % 1 crece, -1 decrece, 0 no importa
    end
end

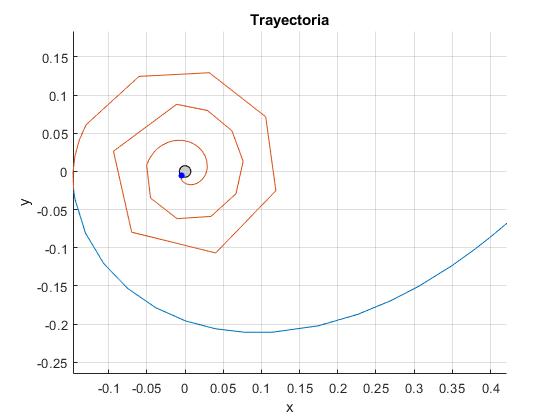
En azul, la trayectoria de la partícula cuendo el cuerpo desciende, en rosa, cuando el cuerpo asciende (se desplaza muy poco hacia arriba)

Actividades

Se introduce

• La longitud l₀ de la cuerda en m, en el control titulado Longitud
• El radio R de la varilla cilíndrica fija en m, en el control titulado Radio
• El cociente de las masas M/m del cuerpo que cuelga y de la partícula, en el control titulado Masa
• Se ha fijado el coeficiente estático y cinético, μ_s=μ_k=0.195
• Se ha fijado el ángulo inicial de la cuerda que hace con la dirección horizontal φ₀=0.1765 (10.1°)

Aunque se trata de us sistema físico sencillo, el cálculo mediante el procedimiento de Runge-Kutta es muy complicado, por lo que es posible que algunas situaciones no se simulen adecuadamente

Se aconseja al lector probar estas situaciones

1. Longitud, l₀=0.44 m, radio R=0.0075 m, masa, M/m=6.49
2. Longitud, l₀=1 m, radio R=0.075 m, masa, M/m=6.49
3. Longitud, l₀=1 m, radio R=0.075 m, masa, M/m=2

El primer caso, corresponde a la sorprendente demostración mecánica

En la parte superior izquierda, se muestra el tipo de movimiento:

• tipo 1, el cuerpo que cuelga (en color rojo) en movimiento, hacia abajo, aunque también puede ser hacia arriba después de haberse desplazado
• tipo 2, el cuerpo que cuelga en reposo

Cuando el cuerpo está en reposo, la energía se conserva. El programa calcula en cada instante el tanto por ciento de error relativo en la energía o el cociente

${\displaystyle \left|\frac{E-E_0}{E_0}\right|·100}$

donde E es la energía en cualquier instante t y E₀ es la energía inicial.

En la parte derecha, se muestran los datos de

• El tiempo, t
• La posición de la partícula (en azul), (x, y)
• El ángulo φ en radianes
• La altura h del cuerpo por debajo del origen, que mide la regla situada a la izquierda
• La velocidad dh/dt de dicho cuerpo, cuando se desplaza hacia abajo la velocidad es positiva, hacia arriba es negativa.

Cuando la partícula está cerca de la varilla, las aceleraciones son muy grandes y los errores de cálculo se acrecientan, tal como puede comprobarse en la parte inferior derecha

Referencias

Qinghao Wen, Xiucai Huang, Yansheng Zhang, Etienne Ong. Looping pendulum: theoretical and experimental studies. Eur. J. Phys. 42 (2021) 014001

A. R. Marlow. A surprising mechanics demonstration. Am. J. Phys. 59, (10) October 1991, pp. 951-952.

David J. Griffiths. Comment on "A surprising mechanics demonstration," by A. R. Marlow [Am. J. Phys. 59, 951-952 (1991)]. Am. J. Phys. 60 (10) October 1992, pp. 951-953

R. E. J. Sears. Comment on "A surprising mechanics demonstration," by A. R. Marlow [Am. J. Phys. 59, 951-952 (1991)]. Am. J. Phys. 63 (9) September 1995, pp. 854-855

Problems for IYPT 2019 Poland, n° 14. International Young Physicists' Tournament 2019. Warsaw University of Technology