Energía potencial

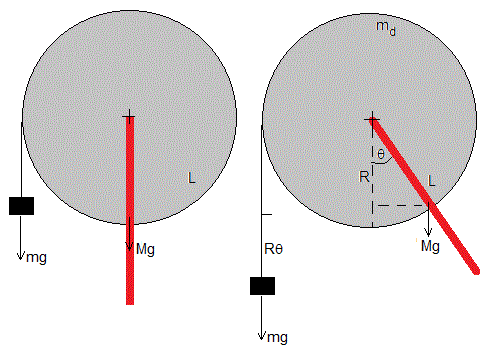
El disco tiene una masa m_d y un radio R. La varilla que gira solidariamente con el disco (en color rojo) tiene una masa M y una longitud L

A medida que el disco gira, la cuerda (inextensible y de masa despreciable) que sujeta al cuerpo de masa m se desenrolla

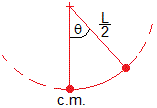
Cuando el sistema ha girado un ángulo θ su energía potencial ha cambiado, el centro de masas del la varilla se ha elevado $\frac{L}{2}-\frac{L}{2}\cos \theta$ y el cuerpo de masa m ha descendido Rθ

La variación de energía potencial es

${\displaystyle E_p\left(\theta \right)=Mg\frac{L}{2}\left(1-\cos \theta \right)-mgR\theta }$

Definimos una energía potencial adimensional V(θ)

${\displaystyle V\left(\theta \right)=\frac{E_p\left(\theta \right)}{mgR}=\frac{MgL}{2mgR}\left(1-\cos \theta \right)-\theta =A\left(1-\cos \theta \right)-\theta ,A=\frac{ML}{2mR}}$

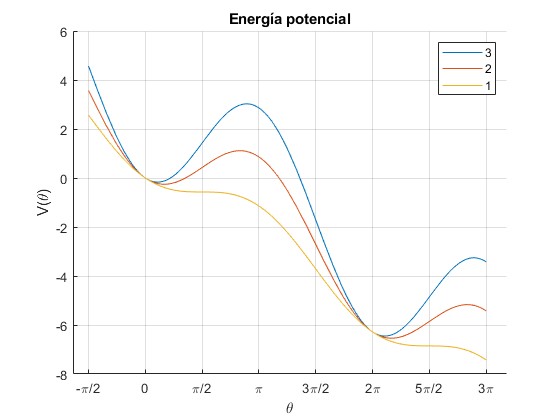
Representamos la función V(θ) para los valores del parámetro A=1, 2 y 3

hold on
for A=[3,2,1]
    fplot(@(x) -x+A*(1-cos(x)),[-pi/2,3*pi],'displayName',num2str(A))
end
hold off
grid on
set(gca,'XTick',-pi/2:pi/2:3*pi)
set(gca,'XTickLabel',{'-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi'})
legend('-DynamicLegend','location','northeast')
xlabel('\theta')
ylabel('V(\theta)')
title('Energía potencial')

Los extremos (máximos y mínimos) de esta función son

${\displaystyle \begin{array}{l}\frac{dV}{d\theta }=-1+A\sin (\theta )=\mathrm{0,}\sin {\theta }_0=\frac{1}{A} \hfill \\ \frac{d^{2}V}{d{\theta }^2}=A\cos (\theta )\hfill \end{array}}$

Los extremos son máximos, cuando la derivada segunda es negativa y son mínimos, cuando la derivada segunda es positiva.

• Los mínimos se producen para θ_n=θ₀+2nπ
• Los máximos para θ_n=π-θ₀+2nπ

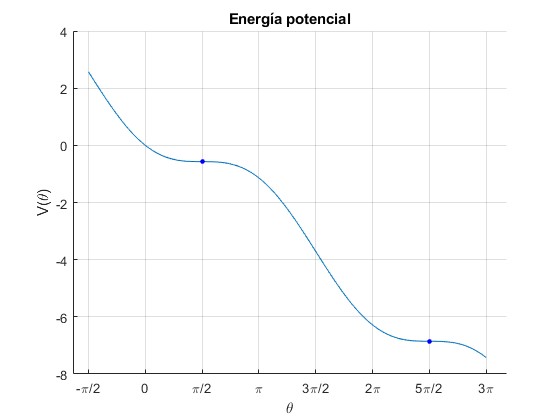
A=3;
f=@(x) -x+A*(1-cos(x));
hold on
fplot(f,[-pi/2,3*pi])
phi=asin(1/A);
for n=0:1
    %mínimos
    plot(phi+n*2*pi,f(phi+n*2*pi),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
    %máximos
     plot((pi-phi)+n*2*pi,f(pi-phi+n*2*pi),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b')
end
hold off
set(gca,'XTick',-pi/2:pi/2:3*pi)
set(gca,'XTickLabel',{'-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2','3\pi'})
grid on
xlabel('\theta')
ylabel('V(\theta)')
title('Energía potencial')

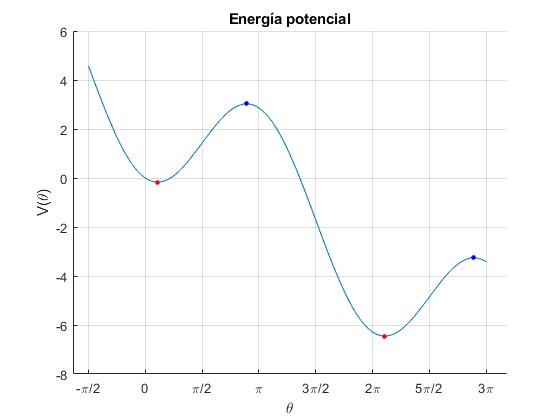
Para A=1, los mínimos y los máximos coinciden y dan lugar a los puntos de inflexión, aquellos en los que la derivada segunda es nula

Posibles movimientos

Supongamos que el parámetro A=4. Para una energía E=2. Calculamos las raíces de la ecuación transcendente utilizando la función fzero de MATLAB

${\displaystyle \begin{array}{l}V\left(\theta \right)=E\\ A\left(1-\cos \theta \right)-\theta -E=0\end{array}}$

function washboard_4
    E=2; %energía
    A=4; %parámetro
    fm=@(x) -x+A*(1-cos(x));
    f=@(x) fm(x)-E;
    x=linspace(-pi/2,3*pi,50);
    r=raices(f,x);
    hold on
    fplot(fm,[-pi/2,3*pi])
    line([-pi/2,3*pi],[E,E],'color','k')
    line([r(1),r(2)],[-8,-8],'linewidth',1.5,'color','r')
    line([r(3),3*pi],[-8,-8],'linewidth',1.5,'color','r')
    line([r(1),r(1)],[-8,fm(r(1))],'lineStyle','--')
    line([r(2),r(2)],[-8,fm(r(2))],'lineStyle','--')
    line([r(3),r(3)],[-8,fm(r(3))],'lineStyle','--')
    disp(r)
    hold off
    set(gca,'XTick',-pi/2:pi/2:3*pi)
    set(gca,'XTickLabel',{'-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi',
'5\pi/2','3\pi'})
    grid on
    xlabel('\theta')
    ylabel('V(\theta)')
    title('Energía potencial')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

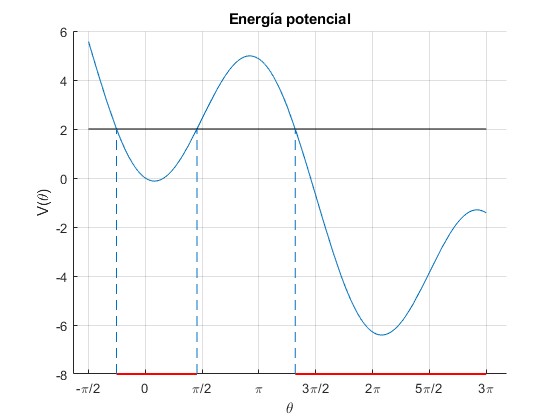
   -0.7966    1.4271    4.1461

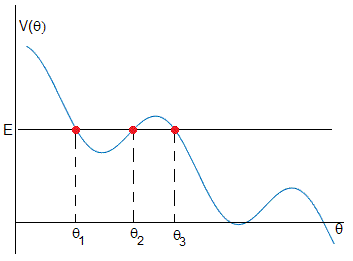
El dispositivo se puede mover en los posiciones θ señaladas por los segmentos de color rojo [-0.7966, 1.4271] y [4.1461,∞). En todas estas posiciones, la energía cinética es positiva, la energía total E es mayor o igual que la energía potencial V(θ)

Ecuación del movimiento

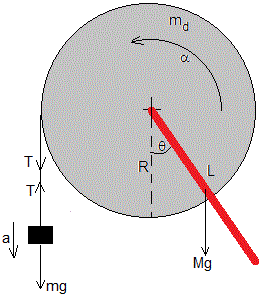
En la figura, se muestran las fuerzas sobre el dispositivo

La ecuación del movimiento del cuerpo de masa m es

${\displaystyle mg-T=ma}$

El momento de inercia del conjunto formado por el disco y la varilla es

${\displaystyle I\text{'}=\frac{1}{2}{m}_d{R}^2+\frac{1}{3}M{L}^2}$

La ecuación de la dinámica de rotación es

${\displaystyle I\text{'}\alpha =TR-Mg\frac{L}{2}\sin \theta }$

La relación entre las aceleración angular α del disco y la aceleración a del cuerpo es

${\displaystyle a=R\alpha =R\frac{d^2\theta }{d{t}^2}}$

Eliminando la tensión T de la cuerda

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_d{R}^2+\frac{1}{3}M{L}^2\right)\frac{d^2\theta }{d{t}^2}=\left(mg-mR\frac{d^2\theta }{d{t}^2}\right)R-Mg\frac{L}{2}\sin \theta \\ \left(\frac{1}{2}{m}_d{R}^2+\frac{1}{3}M{L}^2+m{R}^2\right)\frac{d^2\theta }{d{t}^2}=mgR-Mg\frac{L}{2}\sin \theta \\ I\frac{d^2\theta }{d{t}^2}=mgR-Mg\frac{L}{2}\sin \theta \\ \frac{d^2\theta }{d{t}^2}=-\frac{MgL}{2I}\left(\sin \theta -\frac{2mR}{ML}\right)\\ \frac{d^2\theta }{d{t}^2}=-C\left(\sin \theta -\frac{1}{A}\right)\end{array}}$

El ángulo de equilibrio θ₀ es aquél en el que la aceleración es nula

${\displaystyle \begin{array}{l}\sin {\theta }_0=\frac{2mR}{ML}\\ \sin {\theta }_0=\frac{1}{A}\end{array}}$

Fijados M, L (masa y longitud de la varilla) y R (radio del disco), la masa del cuerpo m ha de ser menor que

${\displaystyle \frac{2mR}{ML}\le \mathrm{1,}m\le \frac{ML}{2R}}$

Resolvemos la ecuación diferencial del movimiento, por el procedimiento ode45 de MATLAB

Fijado el parámetro A=4, para la energía E=2, hemos visto los posibles movimientos del dispositivo estudiando la función energía potencial V(θ)

Supongamos que la partícula parte de r(1)=-0.7966 en reposo. Resolvemos la ecuación diferencial para determinar la posición θ en función del tiempo t

function washboard_5
    E=2; %energía
    A=4; %parámetro
    fm=@(x) -x+A*(1-cos(x));
    f=@(x) fm(x)-E;
    x=linspace(-pi/2,3*pi,50);
    r=raices(f,x);
    f=@(t,x) [x(2); -(sin(x(1))-1/A)]; 
    [t,x]=ode45(f,[0,10],[r(1),0]);
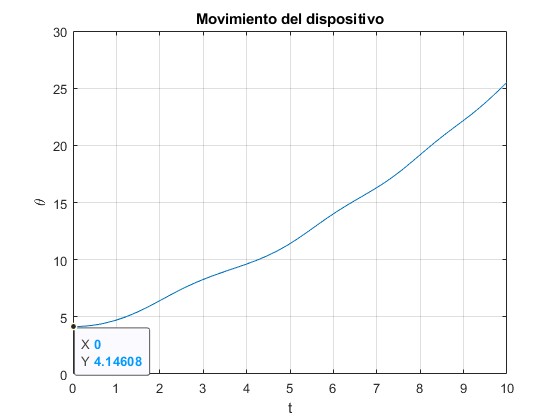
    plot(t,x(:,1))
    grid on
    xlabel('t')
    ylabel('\theta');
    title('Movimiento del dispositivo')
   
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

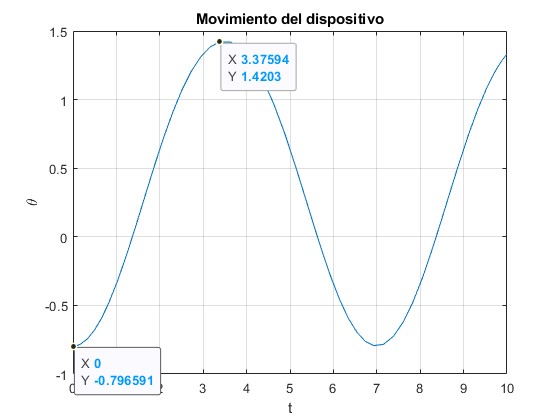
Como apreciamos en la gráfica, la partícula oscila entre las posiciones θ₁=-07966 y θ₂=1.4271

Si se cambia la posición inicial a r(2)=1.4271 de nuevo, la partícula oscila entre θ₂ y θ₁

Si se cambia la posición inicial a r(3)=4.1461, la partícula continua moviéndose hasta θ₂=∞

Actividades

Los datos del dispositivo son

• Masa del disco, m_d=0.36 kg
• Radio del disco, R=0.09 m
• Masa de la varilla, M=0.23 kg
• Longitud de la varilla, L=0.3 m
• Masa del cuerpo, m=0.1 a 0.3 kg

Se introduce

• El valor de la energía total E, en el control titulado Energía
• El valor dede la masa del cuerpo m, en el control titulado Masa. Este valor no puede superar el límite $m\le \frac{ML}{2R}=\frac{0.23·0.3}{2·0.09}=0.3833$

Se pulsa el botón titulado Nuevo

El dispositivo permanece en la posición de equilibrio θ₀

Se pulsa el botón titulado ►

El programa interactivo calcula las raíces de la ecuación transcendente E=V(θ).

Sitúa el dispositivo en cualquiera de las posiciones θ₁, θ₂ o θ₃ determinada de forma aleatoria y lo suelta (parte del reposo)

Si solamente hay una raíz θ₁, lo sitúa en esta posición

A continuación, resuelve la ecuación diferencial del movimiento por el procedimiento de Runge-Kutta, para calcular la posición angular θ en función del tiempo t.

Referencias

M Fiolhais, B Golli, R Nogueira. Mechanical apparatus for the fold catastrophe demonstration. Eur. J. Phys 42 (2021) 045001