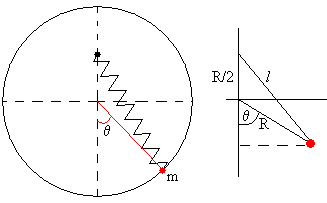
El sistema consiste en una partícula de masa m que se mueve a lo largo de una circunferencia de radio R sin rozamiento. La partícula está unida al extremo de un muelle de constante k, el otro extremo se fija en la posición (0, R/2) tal como se muestra en la figura.

La energía potencial de la partícula se compone de dos términos:

• La energía potencial gravitatoria, mg(R-R·cosθ)
• La energía potencial elástica, debida a la deformación del muelle

La longitud l del muelle deformado es

${\displaystyle l={\sqrt{{(R·\sin \theta )}^2+\left(\frac{R}{2}+R\cos \theta \right)}}^2=\frac{R}{2}\sqrt{5+4\cos \theta }}$

Como la longitud del muelle sin deformar es R/2, la energía potencial debida a ambas fuerzas conservativas es

${\displaystyle \begin{array}{l}{E}_p(\theta )=mgR(1-\cos \theta )+\frac{1}{8}k{R}^2{\left(\sqrt{5+4\cos \theta }-1\right)}^2=\\ mgR\left\{1-\cos \theta +\frac{3\alpha }{8}{\left(\sqrt{5+4\cos \theta }-1\right)}^2\right\}\alpha =\frac{kR}{3mg}\end{array}}$

Representamos la energía potencial E_p(θ) para varios valores del parámetro α: 0.5, 0.9, 1.1 y 1.5. La energía potencial presenta un mínimo para θ=0 cuando α<1 y dos mínimos simétricos ±θ_e para α>1, tal como analizaremos en el siguiente apartado

hold on
for alfa=[0.5,0.9,1.1,1.5]
    f=@(x) 1-cos(x)+3*alfa*(sqrt(5+4*cos(x))-1).^2/8;
    fplot(f,[-pi,pi])
end
set(gca,'XTick',-pi:pi/6:pi)
set(gca,'XTickLabel',{'-\pi','-5\pi/6','-2\pi/3','-\pi/2','-\pi/3',
'-\pi/6', '0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
hold off
grid on
ylim([0.5,2.5])
xlim([-pi,pi])
legend('0.5','0.9','1.1','1.5', 'location','southeast')
ylabel('E_p(\theta)/(mgR)')
xlabel('\theta')
title('Energía potencial')

Posiciones de equilibrio

La fuerza tangencial que actúa sobre la partícula es

${\displaystyle F(\theta )=-\frac{\partial E_p}{\partial \theta }=mgR\left\{\sin \theta -\frac{3\alpha }{2}\left(1-\frac{1}{\sqrt{5+4\cos \theta }}\right)\sin \theta \right\}}$

Las posiciones de equilibrio se obtienen cuando F(θ)=0

θ=0, θ=±π y el ángulo ±θ_e tal que

${\displaystyle \sqrt{5+4\cos {\theta }_e}=\frac{3\alpha }{3\alpha -2}}$

Como -1≤cosθ≤1, el valor mínimo del miembro de la izquierda es 1 y el valor máximo 3. Este valor máximo se obtiene para α=1 y el valor mínimo para α=∞

${\displaystyle \cos {\theta }_e=\frac{-9{\alpha }^2+15\alpha -5}{{\left(3\alpha -2\right)}^2}}$

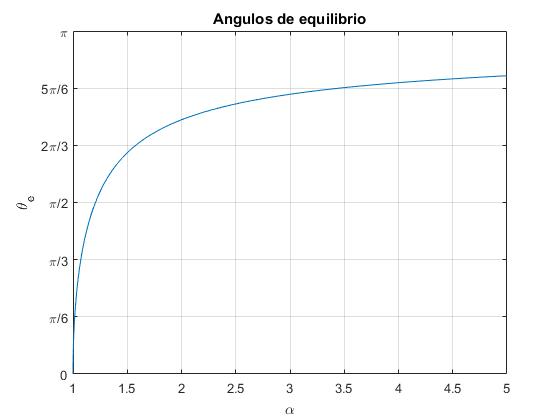
Representamos el ángulo θ_e en función del parámetro α. Vémos que el ángulo θ_e crece rápidamente con α, para tender al valor límite π cuando α→∞

f=@(x) acos((-9*x.^2+15*x-5)./(3*x-2).^2);
fplot(f,[1,5])
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
grid on
ylim([0,pi])
xlabel('\alpha')
ylabel('\theta_e')
title('Angulos de equilibrio')

Estabilidad

Calculamos la derivada segunda de la energía potencial

${\displaystyle \frac{{\partial }^2{E}_p}{\partial {\theta }^2}=mgR\left\{\cos \theta -\frac{3\alpha }{2}\left(1-\frac{1}{\sqrt{5+4\cos \theta }}\right)\cos \theta -3\alpha \frac{{\sin }^2\theta }{{\left(5+4\cos \theta \right)}^{3/2}}\right\}}$

• Para θ=0

${\displaystyle \frac{{\partial }^2{E}_p}{\partial {\theta }^2}=mgR(1-\alpha )}$

La derivada segunda es positiva (mínimo o equilibrio estable) si α<1 y negativa (máximo o equilibrio inestable) si α>1

• Para θ=π

${\displaystyle \frac{{\partial }^2{E}_p}{\partial {\theta }^2}=-mgR}$

La derivada segunda es negativa, por lo que la posición de equilibrio es inestable

• Para θ=±θ_e

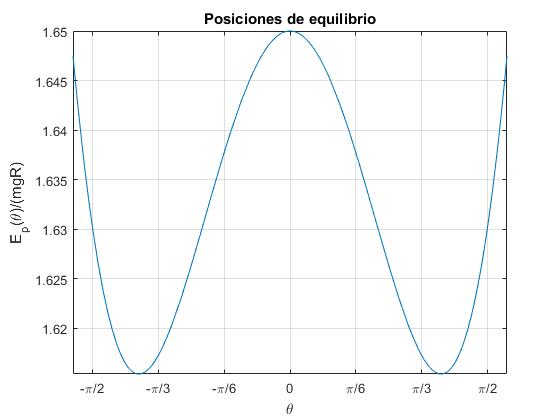
Representamos la energía potencial E_p(θ) para el valor del parámetro α=1.1. La energía potencial presenta mínimos para θ=±θ_e cuando α>1

alfa=1.1;
th_e=acos((-9*alfa^2+15*alfa-5)/(3*alfa-2)^2);
f=@(x) 1-cos(x)+3*alfa*(sqrt(5+4*cos(x))-1).^2/8;
fplot(f,[-th_e-pi/6,th_e+pi/6])
grid on
set(gca,'XTick',-pi:pi/6:pi)
set(gca,'XTickLabel',{'-\pi','-5\pi/6','-2\pi/3','-\pi/2','-\pi/3',
'-\pi/6', '0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
ylabel('E_p(\theta)/(mgR)')
xlabel('\theta')
title('Posiciones de equilibrio')



${\displaystyle \frac{{\partial }^2{E}_p}{\partial {\theta }^2}=-mgR\frac{6{\alpha }^3-11{\alpha }^2+6\alpha -1}{{\alpha }^2(3\alpha -2)}=-mgR\frac{(\alpha -1)(3\alpha -1)(2\alpha -1)}{{\alpha }^2(3\alpha -2)}}$

Esta función es positiva para α>1, por lo que ±θ_e son posiciones de equilibrio estable

Movimiento de la partícula

Deducimos las ecuaciones del movimiento de la partícula alrededor de una posición de equilibrio estable

La partícula se mueve a lo largo de una circunferencia de radio R, su energía cinética es

${\displaystyle E_k=\frac{1}{2}m{\left(R\frac{d\theta }{dt}\right)}^2}$

La lagrangiana L=E_k-E_p

${\displaystyle L=\frac{1}{2}m{\left(R\frac{d\theta }{dt}\right)}^2-mgR\left\{1-\cos \theta +\frac{3\alpha }{8}{\left(\sqrt{5+4\cos \theta }-1\right)}^2\right\}}$

La ecuación del movimiento

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{d^2\theta }{d{t}^2}+\frac{g}{R}\left\{1-\frac{3\alpha }{2}\left(1-\frac{1}{\sqrt{5+4\cos \theta }}\right)\right\}\sin \theta =0\end{array}}$

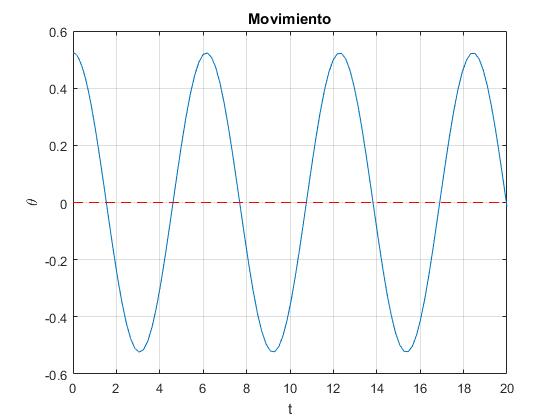
Resolvemos la ecuación del movimiento por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, el móvil parte de la posición θ₀, en reposo, dθ/dt=0

• α<1. La línea a trazos marca la posición de equilibrio estable

alfa=0.9;
R=1;
x0=[pi/6,0];
f=@(t,x) [x(2);-9.8*(1-3*alfa*(1-1/sqrt(5+4*cos(x(1))))/2)*sin(x(1))/R]; 
[t,x]=ode45(f,[0,20],x0);
plot(t,x(:,1))
line([0,20],[0,0],'lineStyle','--','color','r')
grid on
xlabel('t')
ylabel('\theta')
title('Movimiento')



• α>1. La línea a trazos marca la posición de equilibrio estable

alfa=1.1;
th_e=acos((-9*alfa^2+15*alfa-5)/(3*alfa-2)^2);
R=1;
x0=[pi/6,0];
f=@(t,x) [x(2);-9.8*(1-3*alfa*(1-1/sqrt(5+4*cos(x(1))))/2)*sin(x(1))/R]; 
[t,x]=ode45(f,[0,20],x0);
plot(t,x(:,1))
line([0,20],[th_e,th_e],'lineStyle','--','color','r')
grid on
xlabel('t')
ylabel('\theta')
title('Movimiento')



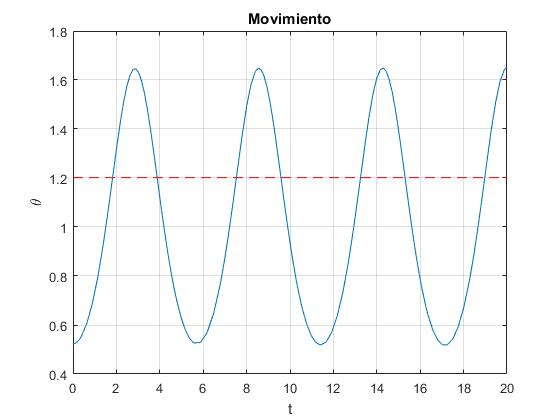
Comprobamos que la energía total permanece constante

${\displaystyle E=\frac{1}{2}m{\left(R\frac{d\theta }{dt}\right)}^2+mgR\left\{1-\cos \theta +\frac{3\alpha }{8}{\left(\sqrt{5+4\cos \theta }-1\right)}^2\right\}}$

>> E=(R*x(:,2)).^2/2+9.8*R*(1-cos(x(:,1))
+3*alfa*(sqrt(5+4*cos(x(:,1)))-1).^2/8)
E =   
16.0498
16.0498
....

Actividades

En el programa interactivo se han fijado los valores de:

• La masa de la partícula m=1 kg

• El radio de la circunferencia R=0.5 m

Se introduce

• El valor del parámetro α en el control titulado Parámetro α.
• la posición inicial θ₀ de partida del móvil con velocidad dθ/dt=0

Se pulsa el botón titulado Nuevo.

• Si α<1 la posición de equilibrio es θ_e=0
• Si α>1, el programa interactivo calcula el ángulo de equilibrio θ_e, señalado por una línea de color rojo

A la izquierda, se proporciona los datos del tiempo t y la posición θ de la partícula. A la derecha, se representa la energía potencial E_p(θ) y se proporcionan los datos de la energía total de la partícula que deberá permanecer constante y del ángulo de equilibrio θ_e.

Referencias

Drugowich J. R., Hipólito O. Spontaneous symmetry breaking in a simple mechanical model. Am. J. Phys. 53 (7) July 1985, pp. 690-693

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Questions 13.14, 13.15, pp. 488-492