Curso Interactivo de Física en Internet

Fundamentos Físicos de la Ingeniería de Energías Renovables

La aparición del ordenador personal en la década de los 80 y su difusión en los centros escolares e incluso en los hogares, hizo pensar que este instrumento iba a tener un papel cada vez más preponderante en el sistema educativo, que iba a cambiar el modo en el que se enseñaba y la forma en la que los estudiantes aprendían, tal como afirmaba Alfred Bork (Personal Computers for Education. New York: Harper & Row Publishers, 1985) un pionero en la utilización de los ordenadores en la enseñanza de la Física.

Aunque el ordenador se convirtió en una herramienta imprescindible en el campo de la investigación, su impacto real en el aula no ha llegado a ser tan decisivo como se preveía. Sin embargo, los ordenadores tienen en sí mismos un gran potencial para mejorar el proceso de enseñanza-aprendizaje, a fin de que:

Internet es imprescindible en el campo educativo, no solamente porque se trata de un medio didáctico de posibilidades insospechadas, sino por sus cualidades intrínsecas, el uso eficaz de Internet es una competencia básica en la nueva sociedad del conocimiento: navegar por las páginas web, descargar ficheros, enviar y recibir mensajes, realizar transferencias bancarias, completar formularios, etc., forman parte de nuestras tareas cotidianas.

Antecedentes

Los programas interactivos para la enseñanza de la Física comenzaron a desarrollarse a partir de 1984 en lenguaje BASIC. Para la enseñanza de un determinado tema, el profesor ejecutaba los programas en un ordenador Commodore 64 concectado a un televisor en el aula de medios audiovisuales que disponía el centro en esa época. El principal inconveniente residía en trasladar a los estudiantes desde su aula habitual al aula que disponía de televisor.

Pocos años después, el centro disponía ya de una aula de ordenadores y los estudiantes pasaron de contemplar en un televisor, las animaciones generadas por los programas, a interaccionar con cada programa que se ejecutaba en un ordenador con monitor en color que manejaba un estudiante. Se produjo por tanto, un cambio radical.

Paralelamente, se iba fundamentando esta nueva forma de enseñar algunos temas de Física, complementando la enseñanza tradicional, en la Tesis Doctoral titulada El odenador en la enseñanza de la Física, análisis teórico-experimental y ejemplos ilustrativos dirigida por el profesor de la Facultad de Ciencias de la Universidad del País Vasco, D. Manuel Tello León, y defendida en mayo de 1988

El Servicio Editorial de la Universidad del País Vasco, publicó posteriormente, en 1991, dos versiones del libro Física con odenador: nivel básico y nivel básico y avanzado, que contenían los guiones de los programas desarrollados hasta la fecha, acompañados de discos que contenían el código compilado de dichos programas para ejecutarse en ordenadores personales PC

Durante la década de 1990 a 2000 se sucedieron de forma vetiginosa ordenadores con un procesador cada vez más potente y con más memoria. Los programas interactivos en lenguaje BASIC, se ampliaron y se adaptaron al lenguaje C++, para que fuese posible ejecutarlos en el entorno Windows 95 y posteriores versiones de este sistema operativo

El Curso Interactivo de Física en Internet

La aparición de Internet y del lenguaje Java, que permitía insertar en las páginas web, programas interactivos denominados applets, introducía un cambio radical. Los materiales educativos estarían disponibles en cualquier momento para cualquier usuario que tuviese una conexión a Internet.

En el año 1997, se desarrolló un modelo de página web, para la enseñanza de un concepto, o la solución a un problema de Física de forma interactiva:

El proyecto inicial, financiado por la Comisión Interministerial de Ciencia y Tecnología del Ministerio de Educación y Cultura, finalizó en diciembre de 1998

Desde esa fecha, se ha venido ampliando con nuevos contenidos, se ha perfeccionado y se ha mejorado su apariencia estética, facilidades de navegación, etc. Se han elaborado tres versiones:

El Curso Interactivo de Física trata casi todos los temas que aparecen en un libro de Física General: Unidades y medidas, cinemática, dinámica, dinámica celeste, sólido rígido, oscilaciones, movimiento ondulatorio, fluidos, fenómenos de transporte, física estadística y termodinámica, electromagnetismo, mecánica cuántica.

Aunque cada uno de los programas interactivos tiene unos objetivos concretos y un diseño totalmente diferente, se pueden clasificar en las siguientes categorías:

Estructura y navegación

La tercera versión, emplea HTML5 para definir la estructura de las páginas web y CSS3 para su presentación.

Cada página está dedicada a un determinado tema, problema o fenómeno físico. Por ejemplo, la página que estudia el arco iris o la página que resuelve el problema de una partícula que se mueve en un bucle, problema habitual en los cursos introductorios de Física. Ocasionalmente, se puede dividir en dos páginas una que trata aspectos básicos y otra avanzados.

Las páginas web están divididas en capítulos, cada capítulo en secciones y cada sección en páginas que contienen aspectos básicos o avanzados de la Física a nivel introductorio. Por ejemplo, Movimiento curvilíneo es una sección de Cinemática, que contiene páginas que describen aspectos básicos como el tiro parabólico pero también hay páginas que describen aspectos avanzados como los tiros frontales a canasta en el juego del baloncesto

Las páginas además están relacionadas mediante enlaces o hipervínculos situados en el texto. Por ejemplo al estudiar el movimiento de una partícula cargada en un campo eléctrico, relacionamos páginas del capítulo campo eléctrico con otras de cinemática o dinámica.

Los menús laterales han sido hasta ahora la forma de acceder a los distintos capítulos y a las distintas páginas estructuradas en secciones en cada capítulo. En esta versión, se accede a las páginas mediante menús desplegables situados en la barra superior. De esta barra cuelgan menús flotantes que nos permiten seleccionar rápidamente una página concreta.

La limitación de la anchura de las páginas a 700 pixels facilita su lectura en los dispositivos móviles y también la posibilidad de imprimir las páginas en papel, sin la pérdida de espacio que suponían los márgenes laterales.

Cada página, contiene un resumen o el propósito de la página, la descripción del fenómeno, los fundamentos físicos, incluyendo porciones de código MATLAB para resolver las distintas situaciones, las actividades a realizar con el programa interactivo, cuyo objetivo es conocer el comportamiento del fenómeno físico que se trate, cambiando los valores de algunas de las variables. Finalmente, se incluyen las referencias a las fuentes de información que se han utilizado para elaborar la página.

Las páginas web contienen texto, enlaces a otras páginas, figuras, fotografías, vídeos, fórmulas matemáticas, porciones de código MATLAB y programas interactivos. En HTML5 los vídeos no precisan de un tratamiento específico, como en versiones anteriores, sino que se insertan en la página web de modo similar a una figura.

Las fórmulas matemáticas, es un problema todavía pendiente. El lenguaje estándar MathML en el que se expresan las fórmulas matemáticas no es entendido todavía por todos los navegadores. Se utiliza Mathjax, un complemento escrito en Javascript que muestra las fórmulas matemáticas en todos los navegadores.

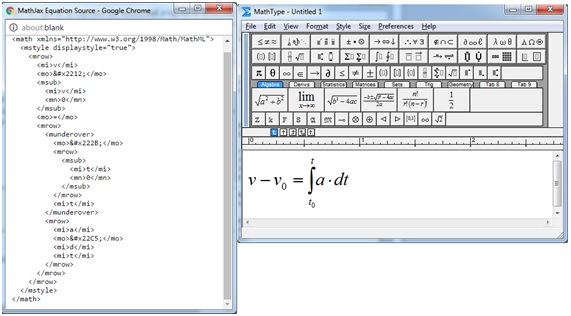
En la imagen, el código MathML de un fórmula matemática insertada en una página web que trata sobre el movimiento rectilíneo y su apariencia en el programa MathType, desde el que se puede editar e incorporar a un documento Microsoft Word.

Los programas interactivos

Los programas interactivos es una nueva forma de transmitir ideas y de enganchar a los estudiantes en actividades educativas. Es una herramienta única para explorar el comportamiento de un sistema que depende del tiempo de un modo que es imposible reproducir en un medio impreso.

Se pueden producir animaciones con apenas interactividad, otras que tiene un alto grado de interactividad con gráficos animaciones o ambas cosas a la vez.

Por motivos de seguridad, los applets de Java tienen cada vez más dificultades para correr en los navegadores actuales. La ventaja de utilizar el estándar HTML5 canvas es que no se precisa de programas externos para interpretar el código, por lo que las simulaciones y animaciones se pueden ver en todos los dispositivos incluyendo tablets y smartphones

El navegador Chrome hace tiempo que no corre applets de Java y Mozilla Firefox desde la versión 52 (marzo de 2017). Por tanto, era necesario volver a programar en el lenguaje Javascript, todos los programas interactivos (alrededor de 650) para que se pudiesen ver en las versiones más recientes de los navegadores.

Java es un lenguaje de programación orientado a objetos completamente distinto de Javascript aunque comparten una sintaxis similar (proveniente del lenguaje C), por lo que ha sido necesario crear un nuevo interfaz de usuario, nuevas funciones, por ejemplo, para resolver una ecuación diferencial o un sistema de ecuaciones diferenciales por el procedimiento de Runge-Kutta, para arrastrar con el puntero del ratón un objeto por la ventana gráfica, etc. y probarlo en numerosos ejemplos.

En cada página web, suele haber un programa interactivo situado en el apartado Actividades.

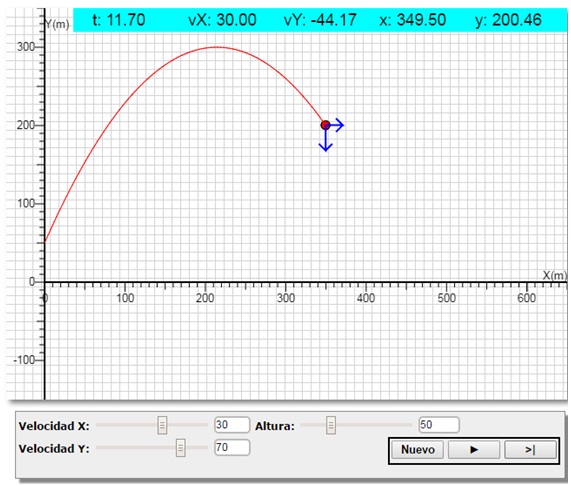
El programa interactivo consta de una región rectangular donde se muestran los gráficos y animaciones denominada canvas y debajo un panel donde se disponen los controles: Velocidad X, Velocidad Y, Altura (para establecer la posición inicial y velocidad inicial del cuerpo que se lanza), tal como se muestra en la figura. En el rectángulo de color negro, se muestran los botones que manejan la animación, que es el mismo para casi todos los programas. Por esta razón, no es necesario proporcionar al estudiante instrucciones o un manual de usuario.

El programa interactivo establece el estado inicial por defecto del sistema. Actuando sobre los controles y pulsando el botón titulado Nuevo, establecemos un nuevo estado del sistema, modificando los valores de algunas de las variables que se describen en el apartado Actividades

Al lado del botón Nuevo disponemos del botón ► que pone en marcha la animación, que se puede detener pulsando el botón pausa cuyo símbolo es ||. Este botón es reemplazado por el botón >|, que nos permite correr el programa paso a paso. Se reanuda la animación pulsando de nuevo, el botón ►.

Selección de contenidos

Una parte de las páginas web del Curso Interactivo de Física, están inspiradas en la experiencia del propio autor, como profesor de Física de primer curso y como creador de programas interactivos para la enseñanza de la Física desde el año 1984. Otra parte, en artículos publicados en las revistas científicas: American Journal of Physics, European Journal of Physics, Physics Teacher, Physics Education, Revista Española de Física, etc.

Por ejemplo, la página web titulada "Simulación de los giros del patinador de hielo", está inspirada en el artículo, Kalotas T. M. Lee A.R. (1990). A simple device to illustrate angular momentum conservation and instability. Am. J. Phys. 58 (1), 80-81, se trata un ejemplo interesante de aplicación del principio de conservación del momento angular. El Curso Interactivo contiene un número elevado de páginas inspiradas en artículos provenientes de la revista American Journal of Physics desde el año 1933 de la publicación de su primer número.

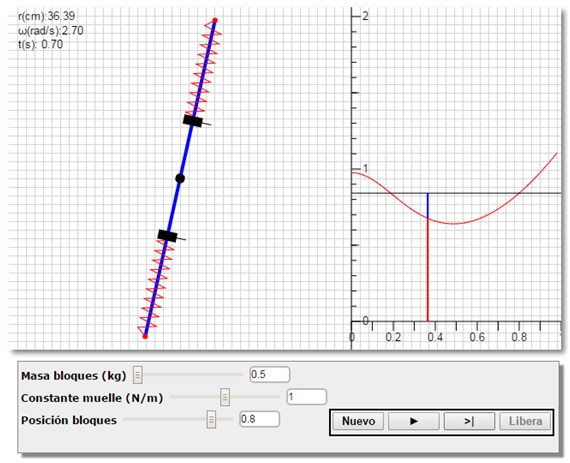
La mayor parte de los libros de texto, cuando introducen el principio de conservación del momento angular, mencionan que un patinador aumenta su velocidad angular de rotación al acercar sus brazos y sus piernas al cuerpo. En esta página web, se describe un modelo de patinador, consistente en un sistema formado por una varilla rígida y dos masas que pueden deslizar sin rozamiento a lo largo de la varilla. La varilla representa el cuerpo y las masas deslizantes los brazos y las piernas, la acción de los músculos se representa por medio de dos muelles que unen los extremos de la varilla con cada una de las masas deslizantes. El sistema puede girar alrededor de un eje perpendicular a la varilla y que pasa por su centro.

A la derecha, se representa la energía potencial efectiva Veff(r) y la energía total E del sistema mediante una recta horizontal. De esta forma asociamos el movimiento del sistema con su energía

Los problemas propuestos en las Olimpiadas Internacionales de Física, Theoretical questions, han sido también una fuente de páginas web. Véase la página titulada Ping pong eléctrico problema propuesto en el año 2004 en Corea del Sur.

En general, se han seleccionado aquellos artículos que ilustran leyes físicas y principios fundamentales, se han transformado en páginas web interactivas agrupadas de forma coherente en una determinada sección de un capítulo del Curso Interactivo.

Modos de usar el Curso Interactivo

Se usará Internet, cuando la exposición de un tema o la realización de ciertas actividades pueda resultar más interesante o instructiva que de la forma habitual que se hace en clase. Algunos ejemplos son los siguientes:

Explicar conceptos 'difíciles'

Cuando se explica un concepto difícil de entender, los gráficos y las animaciones pueden ser muy útiles para mostrar fenómenos que evolucionan en el tiempo o entidades que no se pueden observar directamente como los electrones o las moléculas de un gas.

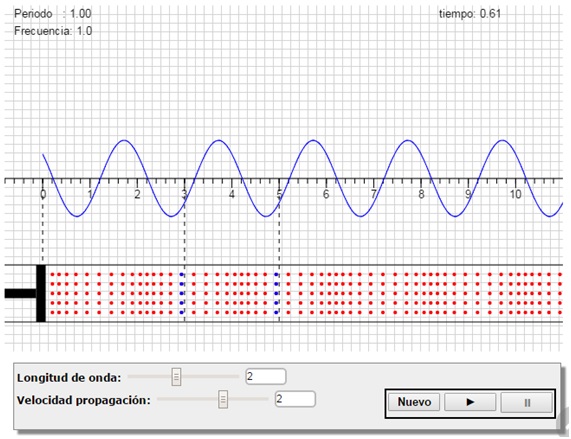
El estudio del movimiento ondulatorio no es fácil para el estudiante, ya que su aspecto cambia con el tiempo. Para explicar este tema, es importante no sólo la representación espacial de la onda en un instante, sino también como va evolucionando temporalmente.

La figura es una imagen tomada de un programa interactivo en el que se representa de forma animada el movimiento de las partículas del medio y la descripción matemática de la propagación del movimiento ondulatorio. Observamos que las partículas de color azul, separadas una longitud de onda vibran en fase.

La siguiente figura es una imagen del resultado de ejecutar un script de MATLAB que calcula los niveles de energía de hasta diez pozos de potencial de anchura y separación dada . El objetivo es el de mostrar la formación de bandas de energía por la adición sucesiva de átomos a la cadena lineal.

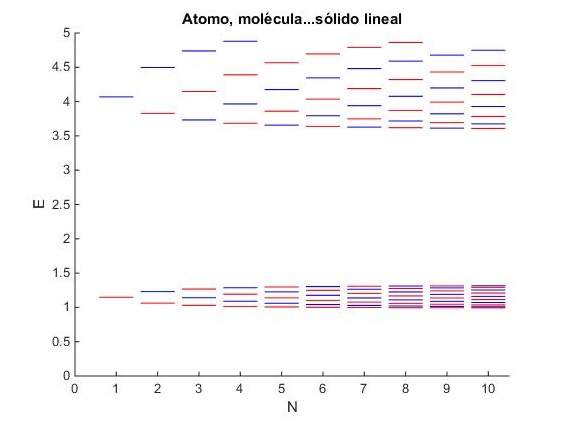
Supongamos que el profesor dispone de un cañón retroproyector conectado a un ordenador en el aula o en una sala de ordenadores. Los programa interactivos proyectados en una gran pantalla constituyen un punto de partida excelente para comenzar la discusión. ¿Qué sucede si se cambia este o el otro parámetro?.

Por ejemplo, un profesor está explicando el capítulo Oscilaciones. Comienza con el caso más sencillo, el Movimiento Armónico Simple. Cambia sucesivamente la amplitud, la frecuencia angular o la fase inicial, observa la animación y la representación gráfica x-t.

Sin embargo, cuando un cuerpo se pone a oscilar, aparecen fuerzas de rozamiento que disminuyen la amplitud de las oscilaciones a medida que transcurre el tiempo. Tenemos las oscilaciones amortiguadas

Cuando el oscilador se conecta a una fuerza oscilante, tenemos un oscilador forzado. Mostrará que el estado estacionario es independiente de las condiciones iniciales y que el estado transitorio dura un determinado tiempo, teóricamente infinito pero que en la práctica viene determinado por el factor de amortiguamiento. Asimismo, mostrará la complejidad del estado transitorio con distintas condiciones iniciales y para distintas frecuencias de la fuerza oscilante.

El profesor, en vez de dibujar figuras estáticas en la pizarra, puede correr los programa interactivos que conectan el comportamiento de los distintos tipos de osciladores (libre, amortiguado y forzado) a su descripción matemática.

Resolver problemas interactivos

La resolución de problemas es una parte esencial de la enseñanza de la Física a nivel introductorio. Observamos que en general, los estudiantes tienen grandes dificultades en la resolución de problemas de Física. Muchos lo intentan pero no son capaces de obtener la solución a partir del enunciado. Muchos factores contribuyen a este fracaso: lingüísticos o de comprensión verbal, falta de entrenamiento suficiente en cursos previos, etc.

En los libros de texto, los enunciados proporcionan toda la información necesaria para resolver un problema. Sin embargo, los estudiantes suelen tener dificultades para su correcta interpretación. Se habrá observado también, que algunos dirigen sus esfuerzos a encontrar la fórmula que contiene los datos que se proporcionan en el enunciado del problema.

Se puede ayudar a los estudiantes a desarrollar mejores estrategias en la resolución de problemas mediante programas interactivos. Observando el comportamiento del sistema físico, se facilita el proceso de análisis, es decir, la descomposición del problema en partes y la aplicación a cada una de ellas, de las ecuaciones que describen el fenómeno físico correspondiente.

La figura muestra el problema del bucle: se lanza una partícula mediante un dispositivo consistente en un muelle elástico comprimido, se desplaza a lo largo de un plano horizontal, describe una trayectoria circular y finalmente, se mueve a lo largo de un plano inclinado.

El enunciado del problema es visual y abierto, de modo que el estudiante puede modificar los datos que el programa proporciona por defecto, pudiendo ensayar otras posibilidades, que le permitirán darse cuenta que la partícula tiene que tener una velocidad mínima en la parte superior de la trayectoria circular para completar el bucle. Se muestra también, mediante un diagrama, cómo la energía inicial de la partícula va disminuyendo debido a la fricción y cómo se va transformando en otros tipos de energía.

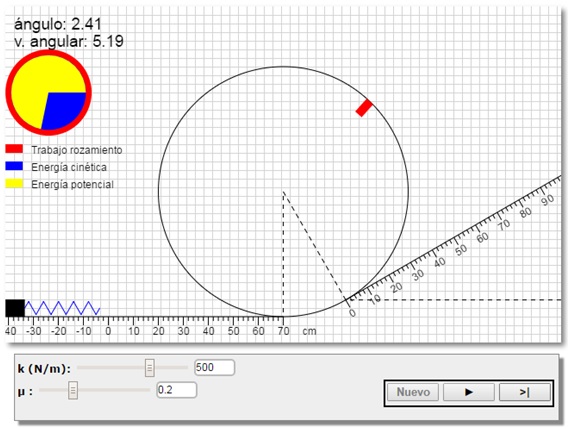
Los estudiantes más adelantados pueden resolver las situaciones que se producen cuando la partícula no consigue describir el bucle. Un script de MATLAB dibuja las trayectorias parabólicas de la partícula.

clear
R=0.5;
ang=(0:10:360)*pi/180;    %dibuja la circunferencia
x=R*cos(ang);
y=R*sin(ang);
hold on
plot(x,y,'black')
axis equal
%trayectorias parabólicas
v0=linspace(sqrt(2*9.8*R),sqrt(5*9.8*R),6);  %velocidad 
fi=asin((v0.^2-2*9.8*R)/(3*9.8*R));  %ángulo de tiro
v1=sqrt(R*9.9*sin(fi));    %velocidad de disparo
tf=4*v1.*cos(fi)/9.8;  %tiempo de vuelo 

for i=2:length(fi)-1       %trayectorias 
    t=linspace(0,tf(i),50);
    x=R*cos(fi(i))-v1(i)*sin(fi(i))*t;
    y=R*sin(fi(i))+v1(i)*cos(fi(i))*t-4.9*t.^2;
    plot(x,y,'red')
end
hold off
xlabel('x')
ylabel('y')
title('El bucle')
grid on

En la figura se muestran, las trayectorias parabólicas seguidas por la partícula, para distintos valores de la velocidad inicial v0 en la parte inferior del bucle.

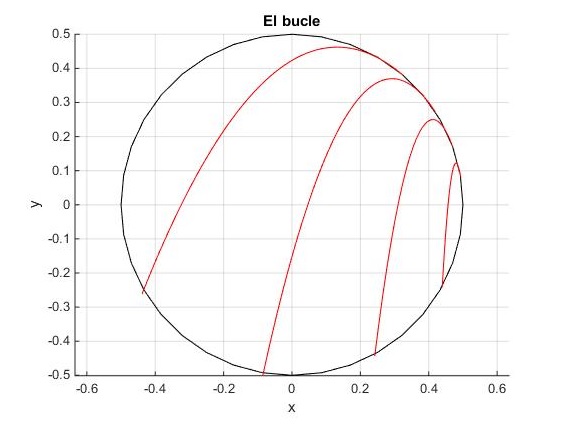
Supongamos que un estudiante está resolviendo en casa o en la sala de estudio, un problema acerca de la caída de los cuerpos con este enunciado u otro similar: Se lanza un objeto hacia arriba con una velocidad inicial de 40 m/s, desde el techo de un edificio de 100 m de altura. Calcúlese la máxima altura que alcanza sobre el suelo y la velocidad con que retorna al mismo.

Conecta el ordenador, carga el Curso Interactivo de Física en el navegador, va al capítulo Cinemática, sección Movimiento rectilíneo, página Caída de los cuerpos. Introduce en los controles los valores iniciales de la velocidad y de la altura del cuerpo, pulsa el botón titulado Nuevo y observa el movimiento. Puede parar la animación pulsando el botón titulado Pausa, o acercarse al instante que alcanza la máxima altura pulsando repetidamente el botón titulado Paso, o al instante que impacta sobre el suelo.

A continuación, resuelve el problema planteando las ecuaciones del movimiento, introduciendo los datos en las ecuaciones y despejando las incógnitas. Finalmente, verifica que sus resultados coinciden con las proporcionadas por el programa interactivo.

La ventaja que proporcionan los programas interactivos es que el estudiante, ve el movimiento de la partícula antes de comenzar a resolver el problema y puede analizarlo, a partir de la observación de las distintas etapas del movimiento del cuerpo.

Realizar 'experiencias' en un laboratorio virtual.

En general, no se recomienda la sustitución de las experiencias reales en el laboratorio por las virtuales en el ordenador. Sin embargo, las experiencias simuladas se pueden emplear como ejercicios previos de preparación para la realización de la experiencia real, ya que la simulación no se ve afectada por la complejidad del dispositivo experimental ni por los instrumentos de medida. El ordenador puede ser aún más útil cuando las experiencias de laboratorio son inaccesibles por ser costosas, peligrosas o difíciles de montar.

La simulación puede limitarse a reflejar los aspectos esenciales o bien, puede ser similar a la experiencia real, tanto en sus elementos constitutivos como en los instrumentos de medida empleados, pero lo más importante es que el procedimiento sea paralelo al real.

En la figura, se muestra la simulación de la medida de la aceleración de la gravedad con un péndulo compuesto, formado por una varilla que puede oscilar alrededor de un eje que perpendicular a la varilla y que pasa por varios puntos (en color rojo) distantes x del centro de masa (en color azul).

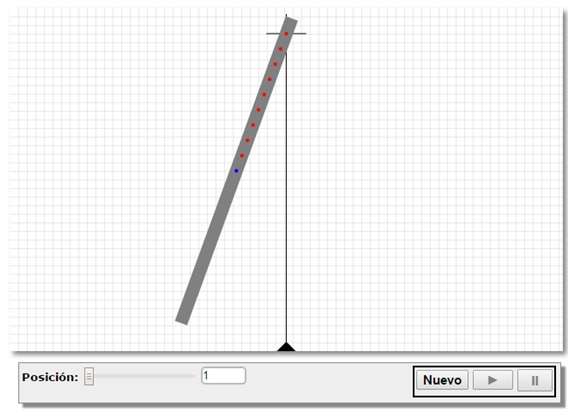
Medimos el periodo Pi de péndulo para cada posición xi, completando una tabla con N pares de datos

x (cm) P (s)
5 2.620
10 1.936
15 1.668
20 1.568
25 1.520
30 1.512
35 1.536
40 1.576
45 1.600

MATLAB nos permite ajustar los datos experimentales del cuadrado del periodo y=P2/(4π2) para cada posición x, a la función no lineal y=a/x+bx mediante la función nlinfit o fminsearch

x=(5:5:45)/100;  
y=[2.620 1.936 1.668 1.568 1.520 1.512 1.536 1.576 1.600].^2/(4*pi^2); 
hold on
%representa los datos experimentales
plot(x,y,'bo','markersize',6,'markerfacecolor','b')
%modelo de función
f_ajuste =@(a,x) a(1)./x+a(2)*x;          
a0=[0.3 4];  %valor inicial de los parámetros
af=nlinfit(x,y,f_ajuste,a0)
%representa la función 
x=linspace(0.04,0.45,100);
y=f_ajuste(af,x);
plot(x,y,'r')
title('Péndulo compuesto')
xlabel('x (m)')
ylabel('P^2/(4·\pi^2)')
hold off

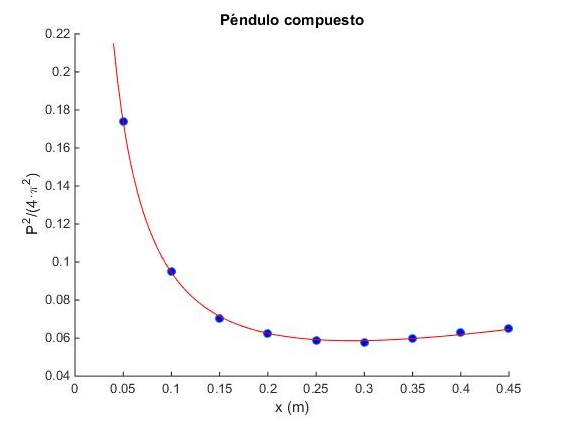
El valor de a es el primer elemento del vector af y el valor de b, el segundo elemento

af =    0.0084    0.1020

Temas complementarios

El Curso Interactivo de Física, ofrece la oportunidad a los estudiantes con un interés especial en explorar distintos temas con mayor profundidad que se hace en clase. Contiene numerosas páginas que no se imparten en un Curso introductorio de Física por falta de tiempo o porque su nivel es excesivamente elevado.

El estudio de la ley de Faraday, es especialmente importante, ya que la producción de electricidad a partir de fuentes renovables es un objetivo prioritario. Se describen los ejemplos básicos que se encuentran en los libros de texto y otros más avanzados.

El tubo de Lenz es una demostración de aula que resulta espectacular para los estudiantes, por el tiempo que demora el imán que se introduce en la parte superior del tubo en aparecer por la parte inferior, en comparación con un objeto no imantado.

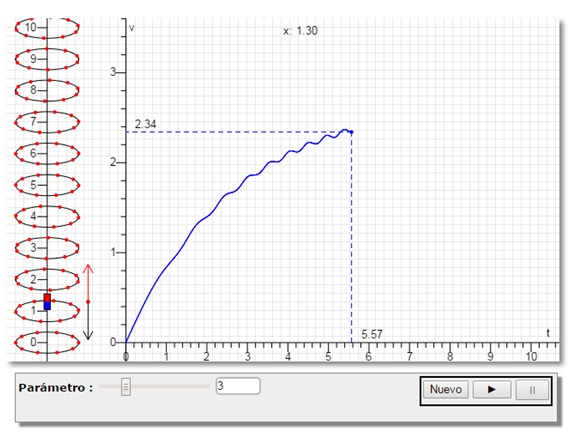
El movimiento de un imán en un tubo metálico vertical es una demostración práctica de los fenómenos de inducción. La fuerza que se opone a la caída del imán es proporcional a la velocidad, de modo que el imán alcanza una velocidad límite constante cuando se desplaza a través del tubo.

Se ha creado una página web para explicar el origen de la fuerza retardadora sobre el imán en términos de las corrientes inducidas en el tubo de metal.

Se resuelve la ecuación diferencial del movimiento del imán, por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante adimensional τ=0, y=y0, dy/dτ=0. El imán parte del reposo desde la posición adimensional y0.

d 2 y d τ 2 =−1−k ∑ j−n+1 j+n (y− y i ) 2 ( (y− y i ) 2 +1) 5 dy dτ 

function a = caida_iman(t,x,k) 
    a=zeros(2,1);
    a(1)=x(2);    
    n=floor(x(1));  %x(1) posición, x(2) velocidad
    temp=0.0;
    for j=n-4:n+5
        temp=temp+(x(1)-j)^2/(1+(x(1)-j)^2)^5;
    end 
    a(2)=-1-k(1)*temp*x(2);
end
x0=zeros(1,2);
x0(1)=10; %valor inicial de x
x0(2)=0; %valor inicial de v;
tf=10; %tiempo final;
k=3; %valor del parámetro
tspan=[0 tf]; 
[t,x]=ode45(@caida_iman,tspan,x0, [],k);

plot(t,-x(:,2))  %x(2) es la velocidad
xlabel('t')
ylabel('v');
grid on
title('Movimiento de un imán en un tubo metálico')

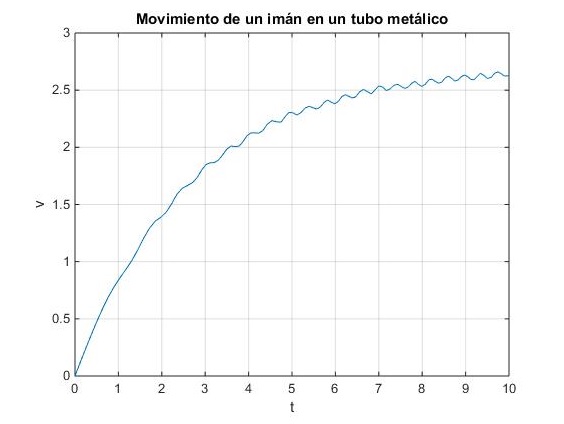
Se explica cualitativamente, el origen de la fuerza retardadora, se elabora un modelo de tubo, formado por espiras conductoras y se determinan las fuerzas que ejercen las corrientes inducidas en las espiras sobre el imán, suponiendo que es un dipolo magnético. Mediante el movimiento de puntos rojos situados en las espiras (portadores de carga positivos) se señala la intensidad y el sentido de las corrientes inducidas en el tubo.

Energías renovables

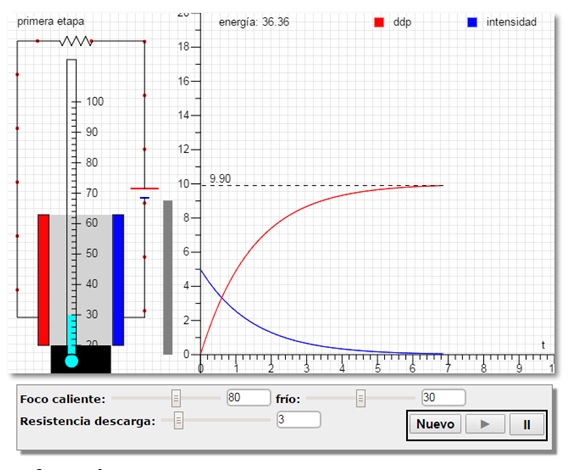
La tercera versión del Curso Interactivo de Física en Internet, subtitulada 'Fundamentos Físicos de la Ingeniería de Energías Renovables', pone el énfasis en las distintas formas de energía y sus transformaciones. Así por ejemplo, la página titulada Transformación de energía térmica en trabajo mediante un condensador, está inspirada en el artículo, E N Miranda. How to transform, with a capacitor, thermal energy into usable work. Eur. J. Phys. 31 (2010) 1457-1462.

La página incluye un programa interactivo, una aplicación HTML5 canvas, que muestra de forma animada el funcionamiento de un condensador lleno de dieléctrico cuando se pone en contacto con un foco frío y un foco caliente.

El curso, contiene páginas dedicadas al estudio de las energías renovables que se irán ampliando con el tiempo.

En el capítulo Sólido rígido, se enseña a los estudiantes el funcionamiento de un giróscopo y se explica que la Tierra es un giróscopo gigante cuyo eje de rotación precesa alrededor del eje perpendicular al plano de la eclíptica con un periodo de 27 725 años formando un ángulo de 23,45°.

En el capítulo Dinámica Celeste, se obtiene la ecuación de la trayectoria de un cuerpo celeste bajo la acción de una fuerza inversamente proporcional a la distancia desde el cuerpo al centro de fuerzas. A continuación, se determina la posición de un planeta en órbita elíptica alrededor del Sol en función del tiempo, el denominado problema de Kepler.

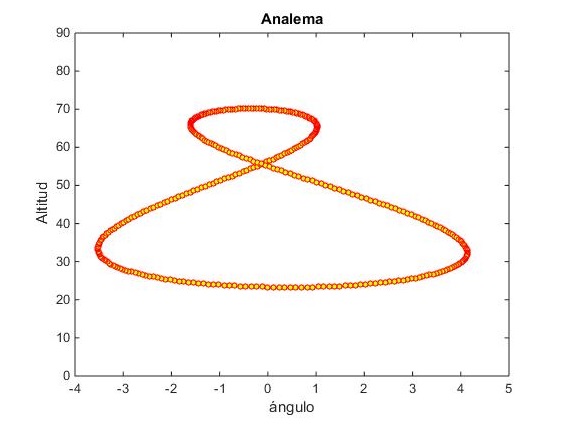
El análisis del recurso solar, comienza con el cálculo de la posición del Sol en función del ángulo horario, en el sistema de referencia local. Si situamos nuestra cámara fotográfica en la misma posición, tomamos una fotografía del Sol cada día cuando alcanza la máxima altura y superponemos las fotografías, veremos una figura similar a la de un ocho, denominada analema. En la figura, se muestra la analema para la latitud λ=43.3° de Bilbao. 

lambda=input('Latitud: ');
lambda=lambda*pi/180;
h=12;

%ecuación del tiempo en minutos
eq_time=@(x) 229.18*(0.00075+0.001868*cos(x)-0.032077*sin(x)
-0.014615*cos(2*x)-0.040849*sin(2*x));
%declinación
delta=@(x) 0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)
+0.000907*sin(2*x)-0.002697*cos(3*x)+0.001480*sin(3*x);

%convierte minutos a grados
N=1:365;
x=2*pi*(N-1-(h-12)/24)/365;
alfa=90-(lambda-delta(x))*180/pi;
gamma=eq_time(x)*15/60; %60 minutos, 1 hora son 15 grados
plot(gamma,alfa,'-ro','markersize',4, 'markerfacecolor','y');

ylim([0 90])
xlabel('ángulo')
ylabel('Altitud')
title('Analema')

Se incluirán en el Curso Interactivo de Física en Internet los temas de energías renovables, que tengan una relación directa con la física básica. Por ejemplo, se explican los fundamentos físicos del sistema EWICON (Electrostatic Wind Energy Converter) que convierte directamente la energía del viento en energía electrostática. Se trata de un sistema que posiblemente no tenga viabilidad comercial, pero tiene una gran riqueza desde el punto de vista de la física: Movimiento de partículas cargadas en un campo eléctrico, la acción del viento sobre el movimiento de las partículas, tensión superficial e inestabilidad de Rayleigh, etc., todos estos aspectos son tratados en las páginas del Curso.

Procedimientos Numéricos con MATLAB

MATLAB, acrónimo que significa MAtrix LABoratory, es un software extraordinariamente potente para la realización de cálculos numéricos, representaciones gráficas y tratamiento de datos. El objetivo de MATLAB es la resolución de un amplio espectro de problemas de forma analítica o numérica utilizando métodos basados en el cálculo matricial.

Proporciona un conjunto de procedimientos codificados en forma de llamadas a funciones y comandos que nos permiten resolver problemas complejos con gran facilidad y flexibilidad. MATLAB consiste esencialmente en:

Además MATLAB dispone de las denominadas toolboxes. Cada toolbox está orientado a una aplicación específica, proporciona un entorno visual y un conjunto de funciones para resolver problemas de un determinado ámbito.

Dado que MATLAB integra el cálculo, visualización y programación en un entorno sencillo de usar y que los problemas y sus soluciones se pueden expresar de una forma flexible, entendible por los estudiantes sin los estrictos requerimientos de los lenguajes clásicos como Java, C++, etc; la utilización de MATLAB tiene las siguientes ventajas:

El aspecto negativo es que MATLAB no es un software de libre distribución. Los costes de las licencias para profesores y estudiantes no son elevados en comparación con las licencias comerciales. Muchas universidades disponen de licencias de Campus, los profesores y estudiantes disponen de forma gratuita de la colección de programas y herramientas que componen MATLAB.

Para que sea posible utilizar MATLAB en la enseñanza de las asignaturas del Grado es necesario que los estudiantes adquieran una formación básica suficiente en la asignatura Informática de primer curso. Al menos, en los aspectos siguientes:

Se han elaborado y publicado en Internet los siguientes materiales a los que se accede seleccionado en el menú MATLAB

En la tercera versión del Curso Interactivo de Física, se utiliza MATLAB como una calculadora programable avanzada: que representa gráficamente funciones, que ayuda a progresar sin error en cálculos complejos con expresiones algebraicas, que aplica procedimientos numéricos a situaciones que no se puede resolver de forma analítica y para el tratamiento de datos.

Ajuste de datos a funciones armónicas

Se emplea el procedimiento de mínimos cuadrados para ajustar un conjunto de datos (ti,xi) a la función

x= A0+A1cos(ωt)+ B1sin(ωt)

El criterio de ajuste se toma como aquél en el que la desviación cuadrática media sea mínima. Se resuelve el sistema de tres ecuaciones con tres incógnitas para obtener el valor de los coeficientes A0, A1,B1.

La temperatura media en cada uno de los meses del año en un cierto lugar ha sido la siguiente

Mes Enero Febrero Marzo Abril Mayo  Junio  Julio  Agosto 
Temperatura 18.9 21.1 23.3 27.8 32.2 37.2 38.0 36.1
Mes Septiembre  Octubre  Noviembre  Diciembre 
Temperatura 34.4 29.4 23.3 18.9

El periodo P=12 meses, la frecuencia angular ω=2π/360 rad/dia.

Para crear una tabla (ti,xi), asignamos el valor de la temperatura media del mes al día correspondiente a la mitad del mes, suponiendo que todos los meses tengan los mismos días.

Elaboramos el script traduciendo las fórmulas matemáticas a código MATLAB

t=(1:12)-0.5; 
x=[18.9 21.1 23.3 27.8 32.2 37.2 38.0 36.1 34.4 29.4 23.3 18.9];
w=2*pi/12;

M=[length(t), sum(cos(w*t)), sum(sin(w*t))
sum(cos(w*t)), sum(cos(w*t).^2), sum(sin(w*t).*cos(w*t))
sum(sin(w*t)),sum(sin(w*t).*cos(w*t)), sum(sin(w*t).^2)]

C=[sum(x);sum(x.*cos(w*t));sum(x.*sin(w*t))];
A=M\C

hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
y=@(t) A(1)+A(2)*cos(w*t)+A(3)*sin(w*t);
fplot(y,[t(1),t(end)]);
xlabel('mes')
ylabel('temperatura °C')
title('Ajuste a funciones armónicas')
grid on
hold off

Corremos el script en la ventana de comandos y nos aparece la gráfica en la que se muestran los datos, puntos de color rojo y la función que mejor ajusta a los datos (en color azul).

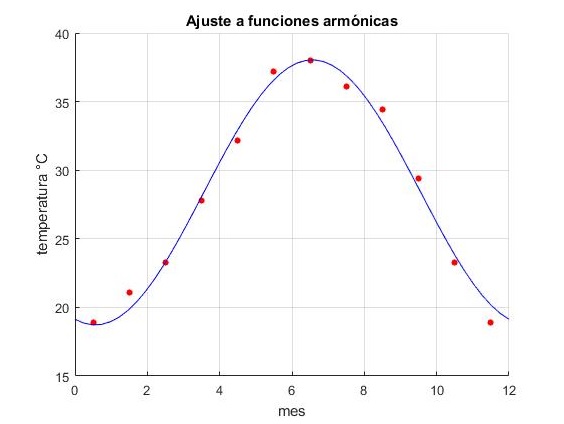
En la ventana de comandos, aparece los valores de los coeficientes A0, A1,B1 de la función 

>> A =
   28.3878
   -9.2559
   -2.8002

La función que mejor ajusta a los datos es

x=28.3878-9.2559cos(πt/6)-2.8002sin(πt/6)

Cálculos con expresiones algebraicas

En la página, titulada Efusión de un gas, para llegar a un resultado, se ha resuelto la integral

∫ 0 ∞ x 4 exp(−α x 2 )dx= 3 8 π α 5

MathSymbolic de MATLAB nos proporciona esta integral, sin tenerla que buscar en los apéndices de algunos libros de Física. 

>> syms x;
>> syms a positive;
>> int('x^4*exp(-a*x^2)',x,0,inf)
ans =(3*pi^(1/2))/(8*a^(5/2))

Análisis de Fourier

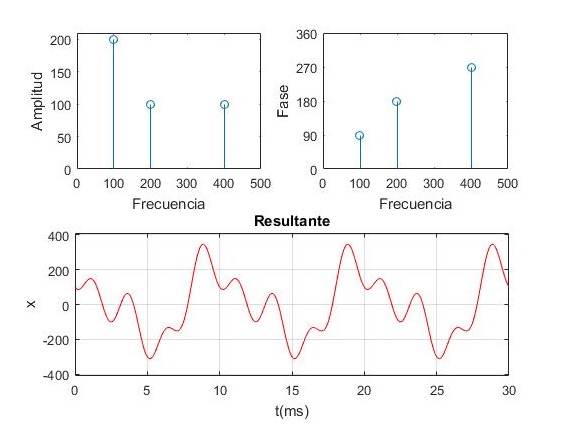
Para introducir al análisis de Fourier, analizamos una función periódica resultado de la superposición de tres funciones armónicas con distintas frecuencias, amplitudes y fases iniciales.

x=200sin(2π·100+π/2)+100sin(2π·200+π)+100sin(2π·400+3π/2)

f=[100,200,400]; %frecuencias
A=[200,100,100]; %amplitudes
phi=[90,180,270]; %fases

subplot(2,2,1)
stem(f,A)
axis([0,500,0,210])
xlabel('Frecuencia')
ylabel('Amplitud')

subplot(2,2,2)
stem(f,phi)
axis([0,500,0,360])
xlabel('Frecuencia')
set(gca,'YTick',0:90:360)
set(gca,'YTickLabel',{'0',90','180','270','360'})
ylabel('Fase')

subplot(2,2,3:4) %resultante
t=(0:0.1:30)/1000; %milisegundos
x=zeros(1,length(t));
for i=1:length(f)
    x=x+A(i)*sin(2*pi*f(i)*t+phi(i)*pi/180);
end
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Resultante')
ylim([-410,410])
set(gca,'XTick',(0:5:30)/1000)
set(gca,'XTickLabel',{'0','5','10','15','20','25','30'})
grid on

Se muestra una ventana dividida en tres paneles, en el que se muestra la función periódica en la parte inferior, y la contribución de los tres armónicos en amplitud, fase y frecuencia.

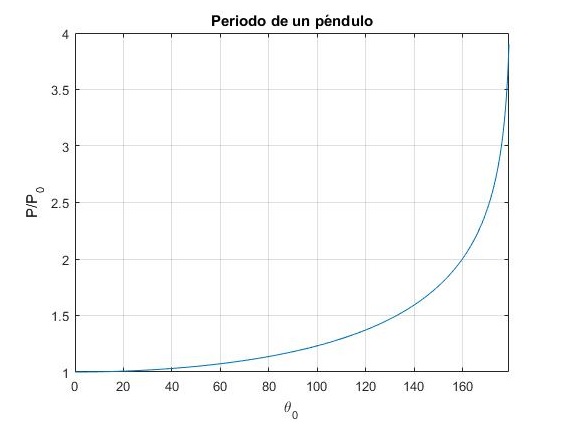
Periodo de un péndulo para cualquier amplitud

El péndulo simple es uno de los ejemplos más estudiados en un curso de Física, es por otra parte, un ejemplo de oscilador no lineal. Muchos problemas en otras ramas de la Física se pueden reducir a la ecuación diferencial que describe el movimiento de un péndulo. El periodo P de un péndulo para cualquier amplitud es

P P 0 = 2 π ∫ 0 π/2 dφ 1− k 2 sin 2 φ

donde P0 es el periodo para las oscilaciones de pequeña amplitud. La integral se denomina elíptica completa de primera especie. Representemos el periodo P/P0 de un péndulo en función de la amplitud θ0 expresada en grados

P=@(x) ellipke(sin(x*pi/(2*180))^2)*2/pi;
fplot(P,[0,179])
xlabel('\theta_0')
ylabel('P/P_0')
title('Periodo de un péndulo')
grid on

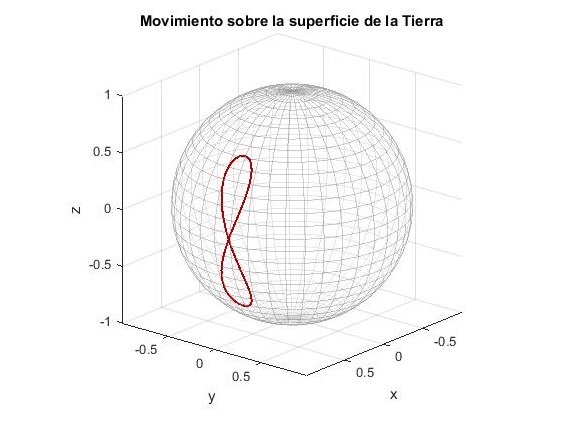
Movimiento relativo de rotación uniforme

Creamos un script, para trazar las trayectorias de una partícula sobre una superficie esférica en movimiento de rotación uniforme, integrando un sistema de dos ecuaciones diferenciales mediante ode45. En la figura (más abajo), se representa la trayectoria seguida por la partícula cuando se lanza hacia el norte con velocidad 0.5.

d 2 θ d t 2 =sinθcosθ( ( dφ dt ) 2 +2Ω dφ dt + Ω 2 ) d 2 φ d t 2 =−2 cosθ sinθ ( Ω dθ dt + dθ dt dφ dt ) 

R=1; %radio de la Tierra
W=1; %velocidad angular de rotación
x0=[pi/3,-0.5,0,0]; %condiciones iniciales: [theta, dtheta/dt, phi,dphi/dt]
tspan=[0,7];
% x(1)=theta, x(2)=dtheta/dt,x(3)=phi, x(4)=dphi/dt
fg=@(t,x)[x(2); sin(x(1))*cos(x(1))*(x(4)^2+2*W*x(4)+W^2); x(4);
 -2*cos(x(1))*(W*x(2)+x(2)*x(4))/sin(x(1))];
[t,x]=ode45(fg,tspan,x0);
xp=R*sin(x(:,1)).*cos(x(:,3));
yp=R*sin(x(:,1)).*sin(x(:,3));
zp=R*cos(x(:,1));
 
%esfera
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5)
axis equal
 
%trayectoria
h1=line(xp,yp,zp);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
view (130,20)
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Movimiento sobre la superficie de la Tierra')

Interacción con los lectores del curso

La ventaja de publicar en Internet reside en que el Curso Interactivo de Física en Internet es un proyecto inacabado, se incorporan cada poco tiempo nuevos temas y se modifican otros. Estos temas se inspiran en cuestiones planteadas en clase, en prácticas de laboratorio, en artículos que aparecen en las revistas científicas. La interacción con los lectores del curso contribuye a su constante mejora.

El profesor de Física tiene en el Curso Interactivo de Física en Internet, un gran repositorio de temas de Física incluyendo los procedimientos numéricos con MATLAB, que puede tomar como punto de partida para sus explicaciones en clase, proyectos para sus alumnos, problemas, etc.. El contenido de las páginas web (texto, figuras y código MATLAB) se puede copiar, pegar y modificar en un procesador de texto como Microsoft Word. Las fórmulas matemáticas están escritas en código MathML, que se pueden copiar y pegar en numerosas aplicaciones, una de ellas MathType, convierte el código en fórmula que puede editarse y por tanto, modificarse para uso personal.

Conclusiones

Se ha creado una nueva versión del Curso Interactivo de Física en Internet que utiliza los estándares más recientes: HTML5 y CSS3 para las páginas web, HTML5 canvas y Javascript para los programas interactivos, de este modo los contenidos del curso se pueden ver en todos los dispositivos incluyendo tablets y smartphones. Incorpora porciones de código MATLAB con el propósito de facilitar que estudiantes realicen cálculos y representaciones gráficas para que puedan analizar el comportamiento del sistema físico en detalle.